Friedrich Balck > Biosensor > Physik > Frequenzsynthese

Beobachtungen:

Frequenzsynthese

Jede periodische Funktion läßt sich aus Bausteinen zusammensetzen.
Als Bausteine kann man (miteinander verwandte) Sinus- und Cosinusfunktionen nutzen, deren Frequenzen ganzzahlige Vielfache einer Grundfrequenz sind. (Fouriersynthese)
Um den Wert der zusammengesetzten Funktion für jeden beliebigen Zeitpunkt zu ermitteln, summiert man die Werte aller Bausteine für diesen Zeitpunkt.
Einstellbare Größen bei diesem Prozeß sind die Gewichte, mit denen jede einzelne Funktion zur Summe beiträgt.
Je nach "Rezept" gibt es unterschiedliche Funktionsverläufe.

In dem nachfolgenden Simulationsprogramm lassen sich die Gewichte der ersten 15 Sinus- und Cosiusfunktionen unabhängig voneinander einstellen (blaue und grüne Schieberegler) und das Ergebnis (die Wellenform) im Fenster rechts ansehen. Es läßt sich nahezu jede Wellenform möglich und als Ton anzuhören.

Das verwendete Programm von Prof. Hwang aus Taiwan, www.phy.ntnu.edu.tw/java/sound/sound.html
liegt auch auf deutschen Schulphysik-Servern bereit. www.schulphysik.de/ntnujava/ waves Fourier Synthesis

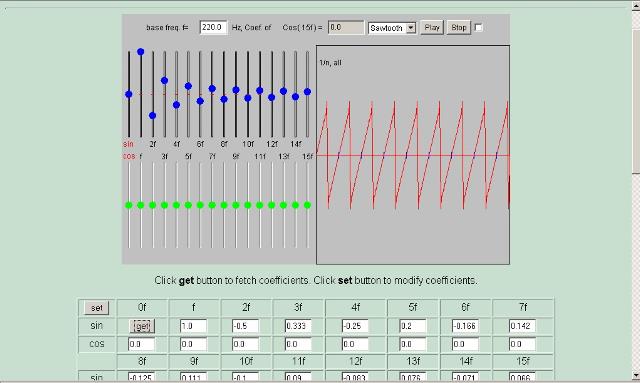Abb. 01: Zusammensetzen eines periodischen Signals aus einzelnen Sinus-Schwingungen unterschiedlicher Amplitude und Phase. Fourier-Synthese
Die Amplitude der einzelnen Komponenten mit den Frequenzen (Grundfrequenz * 1,2,3,4,5,6,7 ...) läßt sich über die blauen Schieberegler einstellen. In der Tabelle ergibt sich für diesen Fall die Zahlenfolge 1, -0.5, 0.333, -0.25 also 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7

Das Ergebnis ist eine Sägezahnschwingung wie bei einer gestrichenen Saite. (FB)

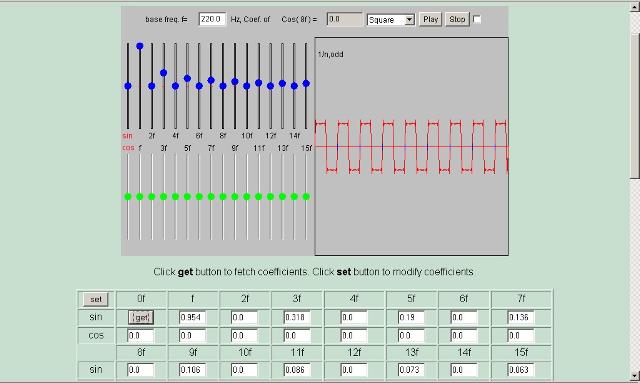Abb. 02: Rechteckschwingung. Die Koeffizienten sind für die Frequenz (n * Grundfrequenz):
1/n, aber nur die ungeraden Zahlen. (FB)

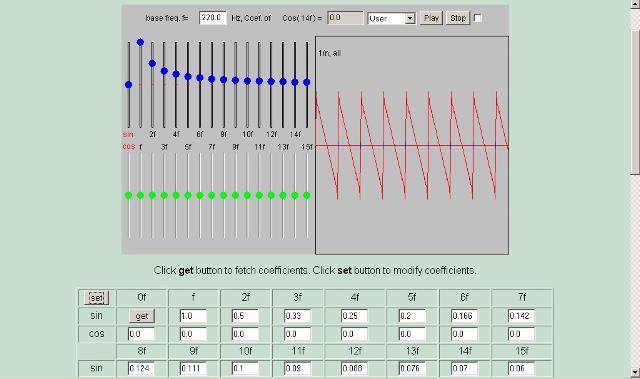Abb. 03: Streichinstrument, steile Flanke, Koeffizienten: 1/n , alle (FB)

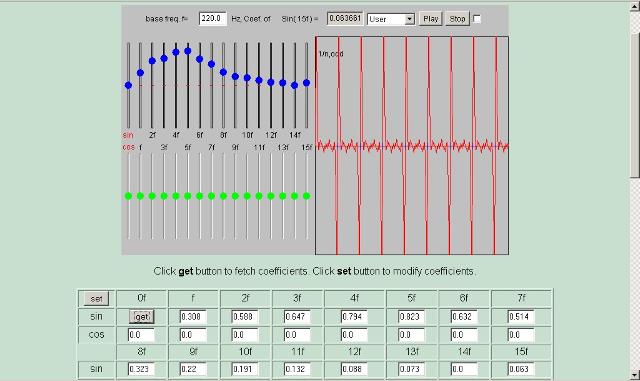Abb. 04: Oboe, Blasinstrument, alle Obertöne, im Bereich n = 4 und 5 sehr starke Amplitude (FB)

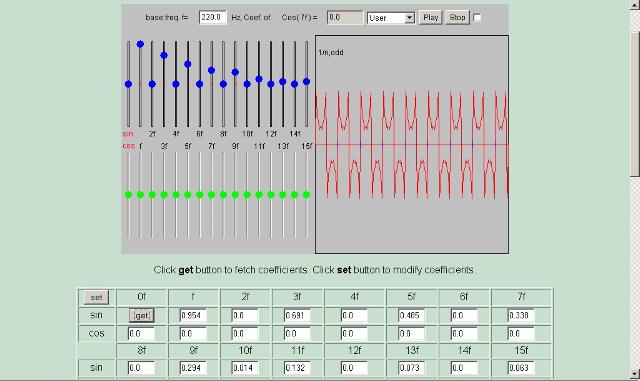Abb. 05: Klarinette, Blasinstrument, nur ungerade Obertöne im unteren Register. (FB)