Beobachtungen:

Hyperschall

In seinem Buch 
zeigt Reiner Gebbensleben ausführlich, wie er mit gut beschriebenen und präzise durchdachten Experimenten Phänomene der Radiästhesie in wissenschaftlicher Weise untersucht hat - wiederholbar und nachvollziehbar.
Auch wenn er als Sensor immer wieder einen biologischen Körper nutzt, zeigen die orts- und zeitabhängigen Aufzeichnungen vieler Experimente, daß die Phänomene reproduzierbar sind. 
Durch geschickte Abschirmmaßnahmen und auf Grund seiner großen Erfahrung hat Gebbensleben die Experimente so durchführen können, daß er den Einfluß von unerwarteten Nebenbedingungen sehr gering halten konnte.

Als äußerst wichtiges Element für die Erforschung der Phänomene ist seine Beobachtung, daß man elektronische Halbleiter, insbesondere die Diode, als "Strahlquelle" im Sinne der Effekte der Radiästhesie nutzen und so gezielt im Labor Experimente zu Winkelabhängigkeiten, Abschwächungen usw. durchführen kann.

Für die Erklärung der Phänomene schlägt er den Begriff Hyperschall vor und meint damit die Aussage, daß die Elektronen bei Stromfluß durch einen Halbleiterübergang Gitterschwingungen (Phononen) im Festkörper auslösen, deren Frequenzen im oberen Gigahertz- bzw. bei vielen Terahertz-Bereich liegen, einem meßtechnisch wenig untersuchten Frequenzbereich.
Es scheint so, daß sich diese Schwingungen außerhalb der Halbleiter auch in Gasen, Flüssigkeiten und Festkörpern ausbreiten und von biologischen Sensoren wahrgenommen werden.

Sensoren hat Gebbensleben bei 82 Röhrenknochen im menschlichen Körper gefunden.
Als Beispiel für seine Arbeitsweise seien exemplarisch einige Abbildungen aus dem Buch beigefügt.

Für seine Argumentation zur Entstehung und Verbreitung des Hyperschalls sei auf die ausführliche Behandlung im Buch verwiesen.



/Gebbensleben 2010/

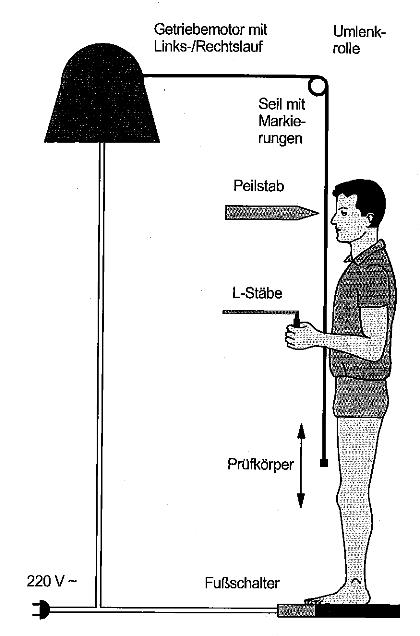Abb. 01: Wo ist der Sensor im Oberschenkel? Ein Prüfkörper wird mit einem Elektromotor so auf und abbewegt, daß der Prüfkörper am Oberschenkel entlang fährt. Während der Bewegung wird der Ausschlag der L-Ruten notiert. Abb. 07.1,   /Gebbensleben 2010/

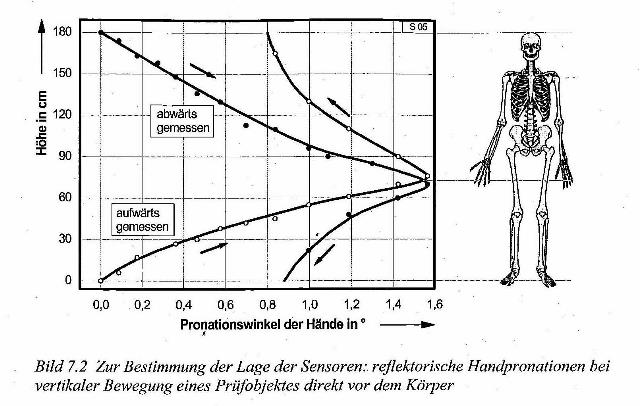Abb. 02: Zur Bestimmung der Lage der Sensoren: reflektorische Handpronationen bei vertikaler Bewegung eines Prüfkörpers direkt vor dem Körper. Bei der Auf- und Abbewegung ergibt sich jeweils ein Maximum an ähnlicher Position, etwa in der Mitte des Oberschenkels.    Bild  07.2,   /Gebbensleben 2010/

Abb. 03:  Untersuchung der Abhängigkeit der radiästhetisch wahrnehmbaren kosmischen Strahlung von Elevationswinkel und Himmelsrichtung mit dem radiästhetischen Teleskop.  Bild 10.7 /Gebbensleben 2010/

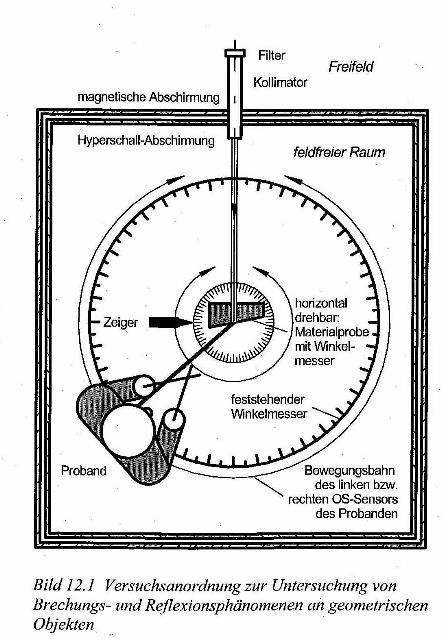Abb. 04:  Versuchsandordnung zur Untersuchung von Brechungs- und Reflexionsphänomenen an geometrischen Objekten, Bild 12,1  /Gebbensleben 2010/

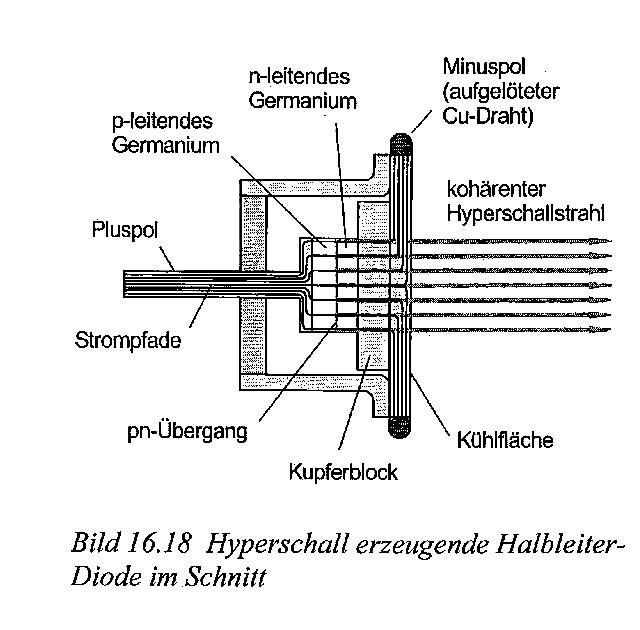Abb. 05: Hyperschall erzeugende Halbleiter-Diode im Schnitt Bild 16.18,   siehe auch Abb. 7.8 und Abb. 10.16 /Gebbensleben 2010/

Abb. 06: Eine Germaniumdiode und ein Aluminiumrohr als Kollimator, freundlicherweise von R. Gebbensleben zur Verfügung gestellt. (FB)

---

Angabe der Meßgröße in dB

R. Gebbensleben hat beobachtet, daß der Winkelausschlag der Ruten bei ihm von der Stärke der spürbaren Effekte abhängt.
Mit zunehmender Stärke wird der Ausschlag größer, d.h. die Spitzen der Stäbe gehen zunächst aufeinander zu, danach überkreuzen sich die Stäbe.

Eigene Untersuchungen hatten beim Autor schon 2007 (vor Erscheinen des Buches von R. G.) ein ähnliches Verhalten mit einer L-Rute gezeigt: Der Ausschlag ist proportional zur Stärke der Anregung  handhabung.htm#motorisch
Es gibt aber auch andere Abhängigkeiten, bei der die z.B. Rute eine Richtung im Raum vorgibt.  handhabung.htm#programmierung

In der Akustik ist es üblich, den Pegel  (Lautstärke) eines Signals auf eine Grundgröße zu beziehen.
 " .... es ist jetzt doppelt so laut wie  ..... " 
Man bezieht also die gemessene Größe A1 auf eine Grundgröße A0, d.h. man bildet das Verhältnis  A1 / A0 und erhält eine dimensionslose Angabe.
Um nicht mit großen Zahlen rechnen zu müssen, bzw. weil das Hörvermögen logarithmisch arbeitet, wird noch der Logarithmus gebildet und mit dem Faktor 10 versehen.
P =  10 log (A1/A0)  
Zur Beschreibung des Rechenverfahrens gibt man für diese dimensionslose Zahl eine "Einheit" an:
Sie lautet:  Bel  oder beim Faktor 10 deziBel  (dB)

Beim Schall bezieht man sich auf eine "Hörschwelle", d.h. die kleinste noch wahrnehmbare Lautstärke A0. Dann sind definitionsgemäß alle gemessenen Werte für A1 größer als A0.
Die Hörschwellen sind bei vielen Menschen unterschiedlich.
Mithilfe von Mikrofonen und elektronischen Anzeigen läßt sich aber ein einheitlicher Wert definieren und als Bezugsgröße verwenden.

In diesem Sinne kann R.G. auch für die spürbaren Intensitäten eine solche Zahl angeben.
Er bezieht den gemessenen Winkelausschlag auf die von ihm gerade noch merkbare spürbare Anregung.
Bei hohen Intensitäten, d.h. wenn die beiden Stäbe fast parallel vor seinem Körper sind, verwendet er einen einstellbaren "Abschwächer" und kann damit den Rutenausschlag wieder zurück in einen gut ablesbaren Bereich zurückführen.

Dies setzt natürlich voraus, daß sowohl die
        Bezugsgröße als auch die körperliche Empfindlichkeit einer Person zu jeder Zeit gleich
sein sollte.
Sind mehrere Rutengeher beteiligt,
       hängen die Angaben auch noch von den individuellen Eigenschaften der Personen ab.

Da sich die Gleichheit nicht garantieren läßt, handelt es sich also um ein
                subjektives Meßverfahren,
                das allerdings Anhaltspunkte über die Stärke der gemuteten Einflüsse
                an bestimmten Orten und Zeiten geben kann.

Abb. 07:   Creation Date (iptc): 2011-07-01T11:48:28 Winkelruten mit Markierungen (FB)

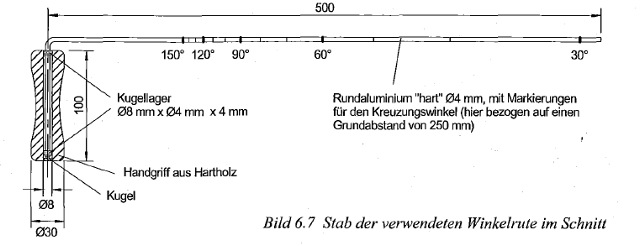Abb. 08: Maße der Winkelrute und Markierungen für ausgewählte Kreuzungswinkel 30°, 60°, 90°, 120° und 150° sowie einige Zwischenwerte /Gebbensleben 2010/

Abb. 09: Überkreuzungswinkel 90°. Mit Hilfe der Markierungen lassen sich die anderen Winkel besser abschätzen. (FB)

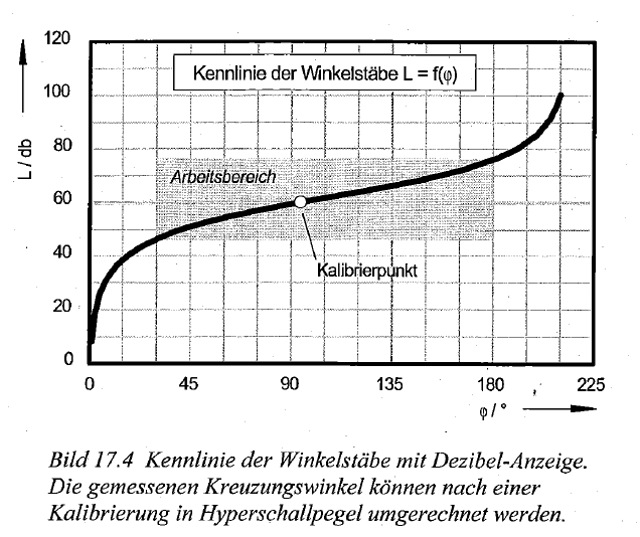Abb. 10: Kennlinie der Winkelstäbe: Umrechnung vom Kreuzungswinkel zur Dezibel-Anzeige. Die Winkelskala reicht auch über 180° (Parallelstellung) hinaus. Zwischen den Kreuzungswinkeln 30° und 180° (grauer Bereich) zeigt die Kurve einen nahezu linearen Anstieg der Werte zwischen 45 dB und 75 dB, d.h. um 30 dB Der Bereich von 30 dB entspricht einer zehnfachen Verdopplung.   10 * 3,01 dB = 30,1 dB (bei einer Verdopplung, d.h. Faktor 2 gilt: log(2) = 0,301       10 log(2) = 3,01 dB)     Abb. 17.04 in /Gebbensleben 2010/

Abb. 11: Experiment mit einer heißen Gasflamme aus Knallgas. Sie erzeugt spürbare Strukturen mit extrem hoher Intensität. Winkelruten in Meßstellung. Vor dem eigentlichen Sensor, dem Oberschenkel, ist ein Abschwächer aus Aluminiumplatten angebracht. Er erlaubt es, auch bei hohen Intensitäten zu "messen". Erfahrung von R.G.: Jede Grenzfläche soll die spürbare Intensität um den Faktor zwei reduzieren. Dies schließt er aus der veränderten Winkelstellung der Ruten. Beim Zwischenschalten von 10 Grenzflächen (5 Aluplatten) müßte sich der Kreuzungswinkel rechnerisch um 30 dB z.B. von 75° auf 45° reduzieren (siehe obiges Zahlenbeispiel bei der Abbildung aus dem Buch 17.4 ). Der "Meßwert" ergibt sich dann aus der Winkelstellung und dem Korrekturfaktor für die Anzahl der Platten.  (FB)

Abb. 12: Abschwächer mit (von links)  10  20  20  15  10 Aluminium Platten, 75 Stück, also 150 Grenzflächen. Damit ließe sich um den Faktor 2 hoch 150 abschwächen. Das entspricht einer Abschwächung von  10 * 150* log(2)  also rund  450 dB (FB)

---

www.biosensor-physik.de

(c)  21.11.2010 -    14.09.2017  F.Balck