Friedrich Balck > Biosensor > Versuche > Magnetfeld-Rechnung

Beobachtungen:

Magnetfeld-Rechnung

1.1 Gerader Draht
1.2 Gerader Draht, bifilar
1.3 gerader Draht, bifilar, mehrfach nebeneinander

2.1 Drahtring, eine Windung, einfach
2.2 Drahtring, eine Windung, bifilar

3.1 Flachspule, einfach
3.2 Flachspule, bifilar

4. Flachspule bifilar, als YinYang-Spule

5. Rechenprogramm

Grau: Draht
grüne Kreuze: Stützpunkte für die Magnetfeldberechnung
rot-blaue Striche: zeigt in Richtung des Magnetfeldvektors, Länge entspricht Wurzel(Intensität)
Faktor: Skalierungsfaktor für die Fähnchen nach dem Wurzelziehen.

Die Objekte ( Draht Ring, Flachspule) für die Rechnung werden mit diskreten Punkten und nicht als kontinuierliches Objekt dargestellt. Daher kann es bei der Berechnung der Magnetfelder nach Biot-Savart zu Artefakten kommen.

1.1 Gerader Draht

Beobachtung:
Fließt durch einen geraden Draht ein Strom, dann gibt es ein Magnetfeld B, dessen Feldlinien ringförmig um den Draht herum verlaufen. "Sie rotieren um den Draht herum."

Mathematisch nennt man es: "Rotation B" und schreibt dafür rot B.
Was physikalisch hinter rot B steckt, beschreibt das Durchflutungsgesetz (eine der vier Maxwellschen Gleichungen)

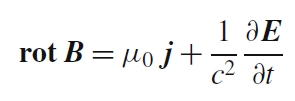
Um einen elektrischen Strom j oder um eine sich zeitlich ändernde elektrische Spannung dE/dt herum gibt es ein Magnetfeld B.

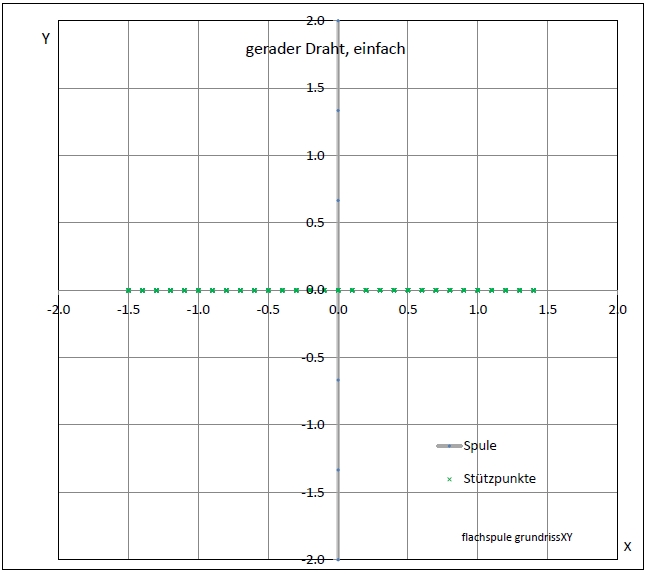Abb. 01-01-01: Grundriss, gerader Draht (FB)

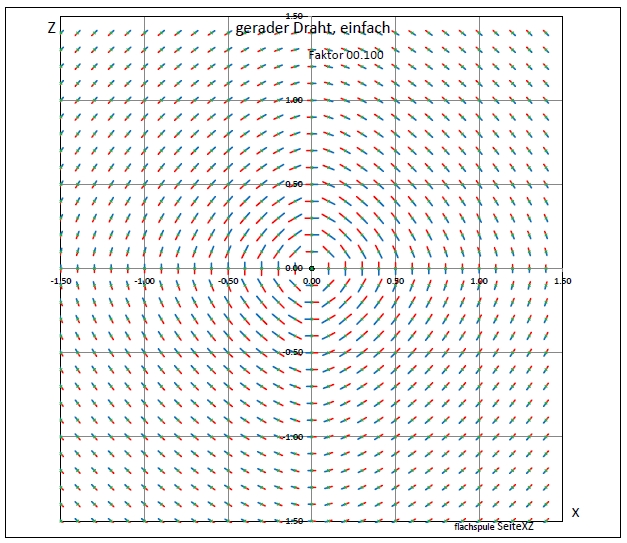Abb. 01-01-02: Seitenansicht, Konzentrische Kreise um den Draht in der Mitte herum.
Wie erwartet gilt hier das Durchflutungsgesetz. (FB)

1.2 Gerader Draht, bifilar

Bei zwei parallelen Drähten mit entgegengesetztem Stromfluß heben sich die Magnetfelder im Fernbereich auf.
Was passiert aber im Nahbereich?

Ergebnis der Rechnungen:

Es bleibt ein kleines Restfeld

ein Wirbelpaar: zwei Wirbel mit umgekehrten Drehsinn
links und rechts von der Mittelachse und
außerhalb der Drähte.
Der Abstand der Wirbelzentren zur Achse nimmt mit der Länge des Drahtes zu.
Je weiter die Drähte voneinander entfernt sind, um so stärker ist das Feld.
Die Wirbel sind im Innenbereich leer, d.h. sie umschließen keinen Strom!

Bei zwei parallelen Stromleiter wäre zu erwarten, daß sich die Wirbel jedes einzelnen Drahtes überlagern und auslöschen.
Im Nahbereich ist dies offensichtlich nicht so. Sie bleiben nebeneinander bestehen.

Was macht ein Paar von zwei "leeren" Wirbel nebeneinander mit der feinstofflichen Materie?

Abb. 01-02-01: Zwei parallele Drähte, am oberen Ende kurzgeschlossen. Der Strom fließt durch den einen Draht von unten nach oben und über den anderen wieder nach unten.
Jeder Draht besteht aus 30 Elementen.
Die Achsen sind unterschiedliche skaliert!
    iDraht = 20
    Bifilar = True
    offSetX = 0.03
    posX = -0.015
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.3
    DarStellung = 4 (FB)

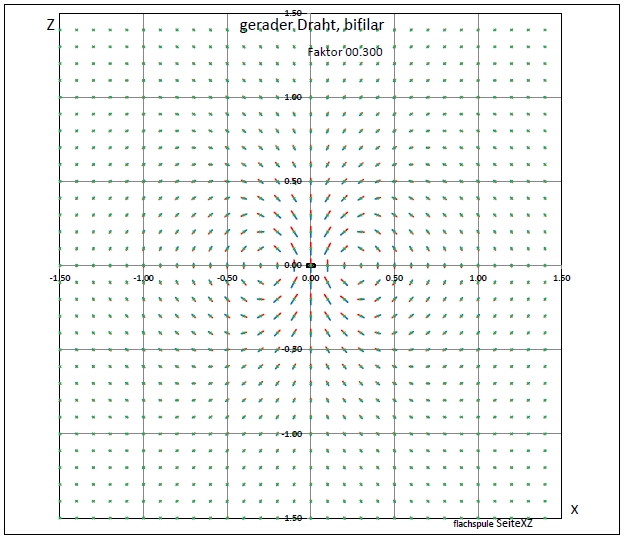Abb. 01-02-02: Übersicht, Wirbel links und rechts von den Drähten
Passend zur der Abbildung vorher.
Draht von y = -10 bis y= +10
iDraht = 20
    Bifilar = True
    offSetX = 0.03
    posX = -0.015
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.3
    DarStellung = 4 (FB)

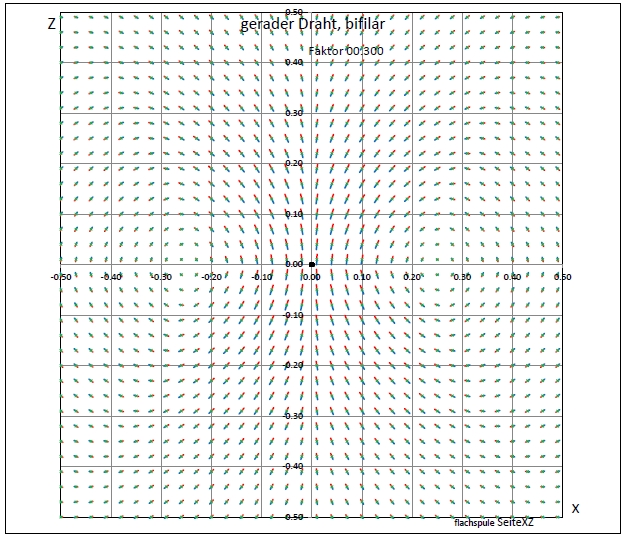Abb. 01-02-03: kleinerer Ausschnitt Zoom, es gibt Wirbel links und rechts außerhalb von den Drähten.
Abstand: 0.002, Skalierung 0.3
Draht von y = -10 bis y= +10
(FB)

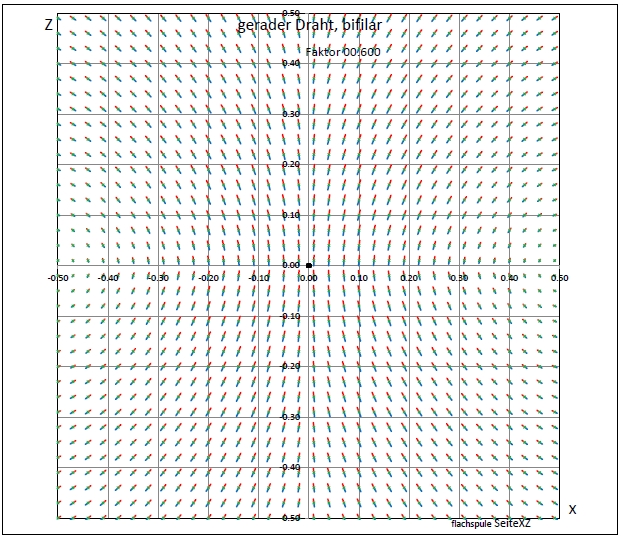Abb. 01-02-04: kleinerer Ausschnitt
Abstand: 0.002, Skalierung 0.6
Draht von y = -20 bis y= +20
Bei längerem Draht liegen die Wirbelachsen weiter außen. (FB)

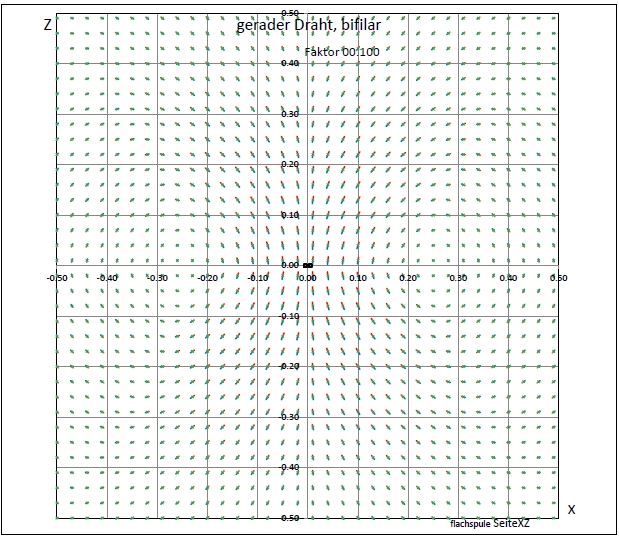Abb. 01-02-05: Abstand: 0.01, Skalierung 0.1
Draht von y = -10 bis y= +10 (FB)

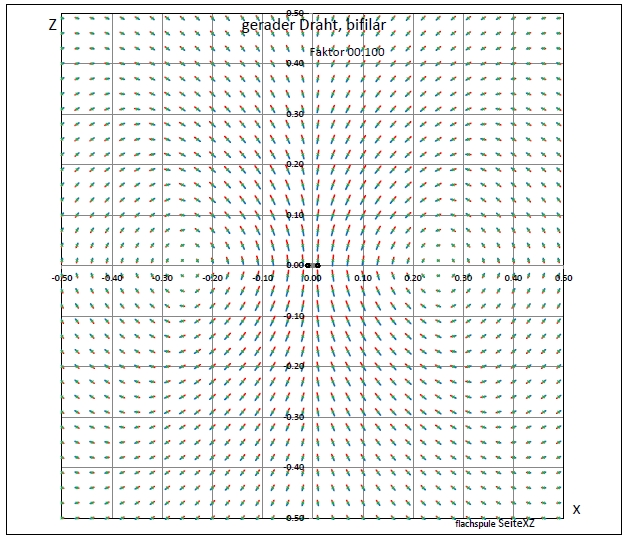Abb. 01-02-06: Abstand: 0.02, Skalierung 0.1
Draht von y = -10 bis y= +10 (FB)

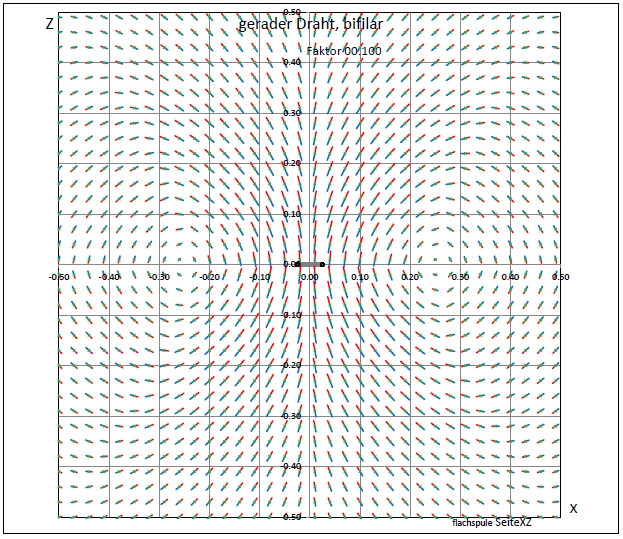Abb. 01-02-07: Abstand 0.05 Skalierung 0.1
Draht von y = -10 bis y= +10 (FB)

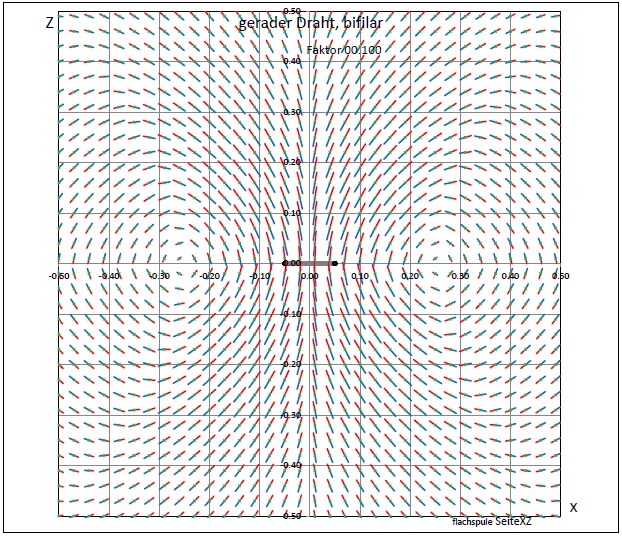Abb. 01-02-08: Abstand 0.1, Skalierung 0.1
Draht von y = -10 bis y= +10 (FB)

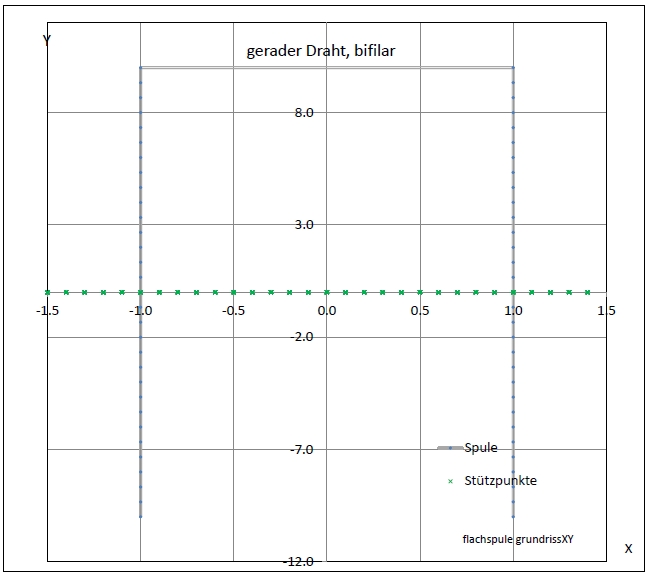Abb. 01-02-09: bifilar, zwei Drähte im Abstand von zwei Metern.
Die Achsen sind unterschiedliche skaliert !!

31 Stützpunkte für jeden Draht, d.h. 30 Elemente, Drahtlänge 20 m, Abstand 2 m

iDraht = 20
    Bifilar = True
    offSetX = 2
    posX = -1
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.05
    DarStellung = 4 (FB)

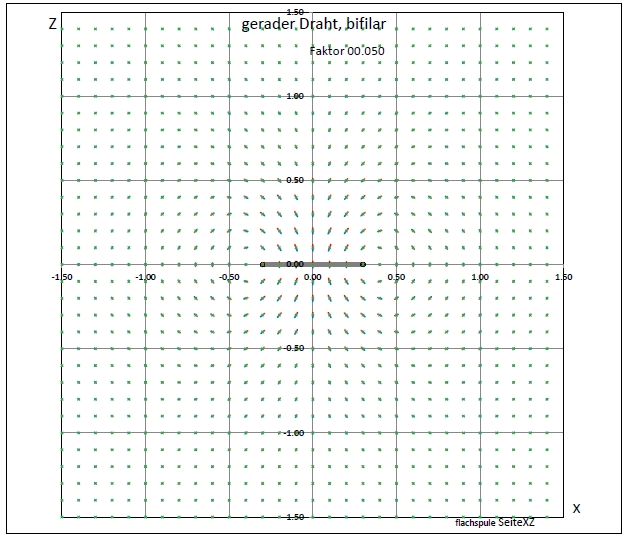
Abb. 01-02-10: Geometrie passend zu Abbildung vorher.
Variation des Abstandes, großer Abstand der Drähte: 2
Die Felder um die beiden Drähte herum sind nahezu unbeeinflußt durch den gegenüberliegenden.
Drahtlänge = 20

    iDraht = 20
    Bifilar = True
    offSetX = 2
    posX = -1
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.05
    DarStellung = 4 (FB)

Abb. 01-02-11: Variation des Abstandes, großer Abstand der Drähte: 0.6
Die Felder der einzelnen Drähte beeinflussen sich. Die Mittelpunkte der Wirbel liegen außerhalb der Drähte.
Drahtlänge = 20

    iDraht = 20
    Bifilar = True
    offSetX = 0.6
    posX = -0.3
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.05
    DarStellung = 4 (FB)

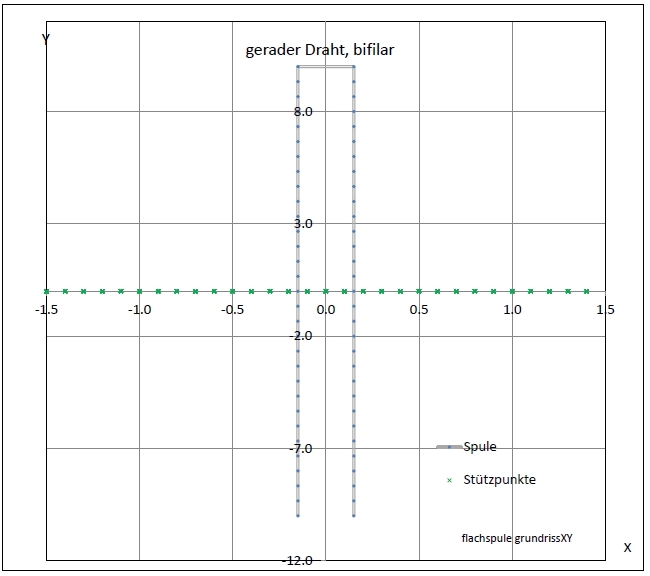Abb. 01-02-12: bifilar, zwei Drähte im Abstand von zwei Metern.
Die Achsen sind unterschiedliche skaliert !!

31 Stützpunkte für jeden Draht, d.h. 30 Elemente, Drahtlänge 20 m, Abstand 0,3 m
iDraht = 20
    Bifilar = True
    offSetX = 0.3
    posX = -0.15
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.05
    DarStellung = 4 (FB)

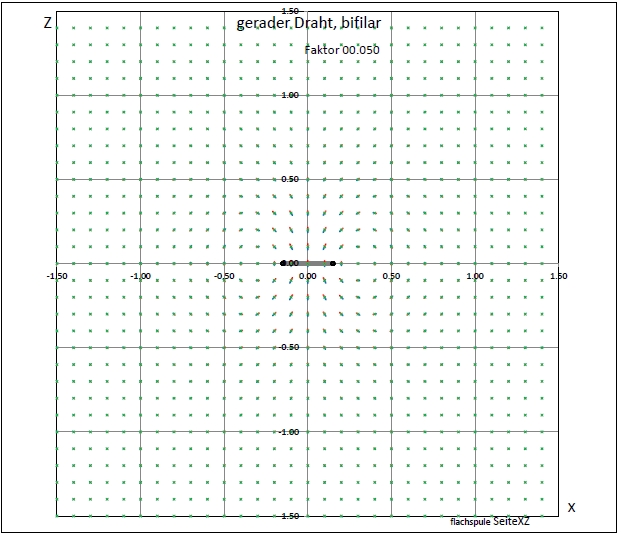Abb. 01-02-13: Geometrie passend zu Abbildung vorher.
Variation des Abstandes, großer Abstand der Drähte: 0.3
Die Mittelpunkte der Felder liegen weit außerhalb.
Drahtlänge = 20

    iDraht = 20
    Bifilar = True
    offSetX = 0.3
    posX = -0.15
    KopfText = "gerader Draht, bifilar"
    Skalierung = 0.05
    DarStellung = 4 (FB)

1.3 gerader Draht, bifilar, mehrfach nebeneinander

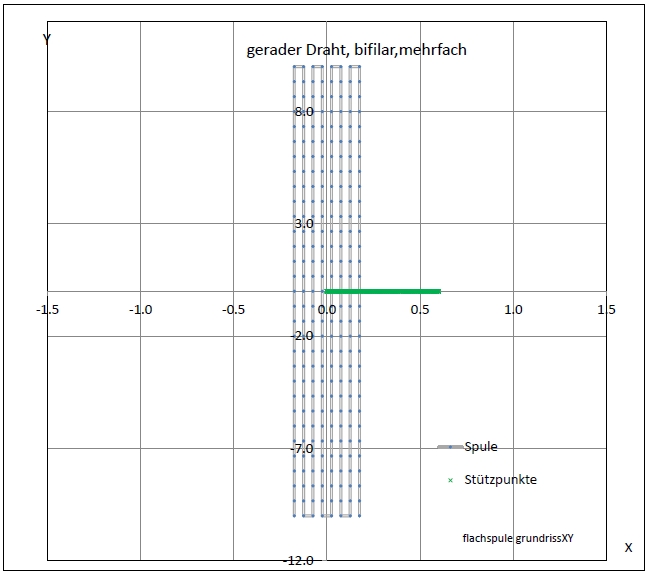Abb. 01-03-01: vier mal zwei bifilare Drähte nebeneinander,
"rauf-runter", "rauf-runter" , "rauf-runter", "rauf-runter"
Jeweils 30 Abschnitte pro Draht.
Die Achsen sind unterschiedlich skaliert! (FB)

flachspule-einfacher-draht-bifilar-mehrfach-seite-01-006.jpg

Abb. 01-03-02: bifilarer Draht, mehrfach

    iDraht = 20
    Bifilar = True
    offSetX = 0.05
    posX = -0.175
    MultiLayer = 3 ' noch einmal das gleiche
    KopfText = "gerader Draht, bifilar,mehrfach"
    Skalierung = 0.6
    DarStellung = 4 (FB)

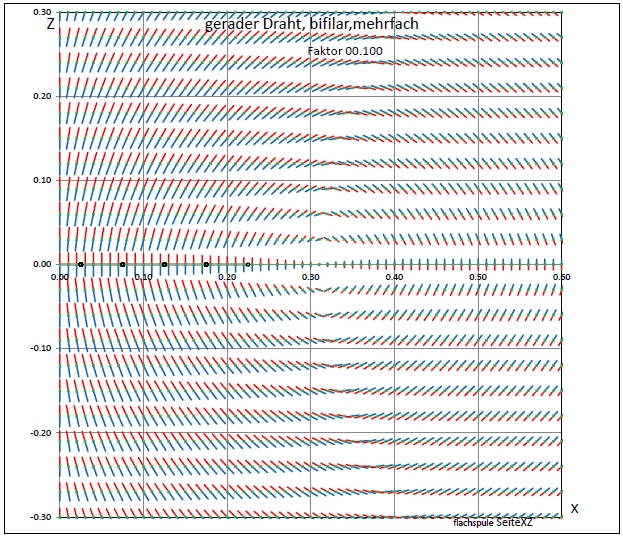flachspule-einfacher-draht-bifilar-mehrfach-seite-02-006.jpg

Abb. 01-03-03: Blick in einen Wirbel
    iDraht = 20
    Bifilar = True
    offSetX = 0.05
    posX = -0.175
    MultiLayer = 3
    KopfText = "gerader Draht, bifilar,mehrfach"
    Skalierung = 0.1
    DarStellung = 6   (FB)

2.1 Drahtring, eine Windung, einfach

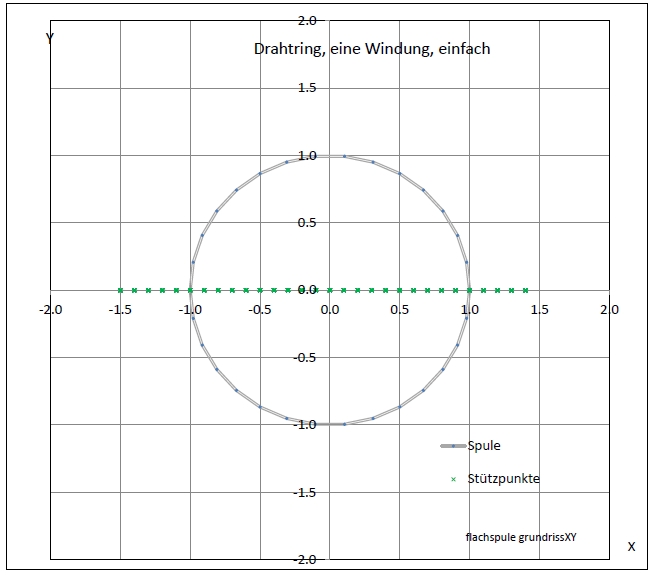Abb. 02-01-01: Einfache Leiterschleife, der Strom fließt im Kreis herum. (FB)

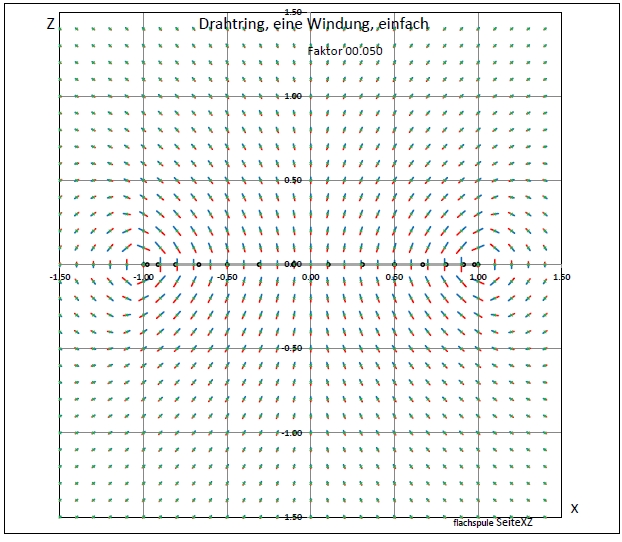Abb. 02-01-02: Es gibt rechts und links Wirbel um den Draht herum. (FB)

2.2 Drahtring, eine Windung, bifilar

Abb. 02-02-01: Zwei Leiterschleifen übereinander. Der Strom fließt zunächst durch die eine Schleife und dann in umgekehrter Richtung durch die andere. (FB)

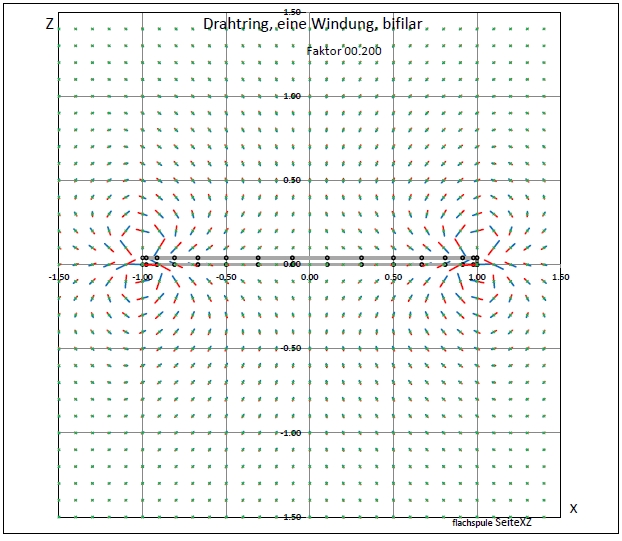Abb. 02-02-02: Es gibt an den Rändern jeweils oberhalb und unterhalb Wirbel, die die Form einer Acht haben. (FB)

Abb. 02-02-03: Vier bifilare Ringe übereinander
    SpulenRadius = 1
    SpulenInnenRadius = 1
    WindungsAbstand = 0
    Bifilar = True
    offSetZ = 0.04
    MultiLayer = 3
    KopfText = " Drahtring, eine Windung, bifilar, mehrfach"
    Skalierung = 0.2
    DarStellung = 4 (FB)

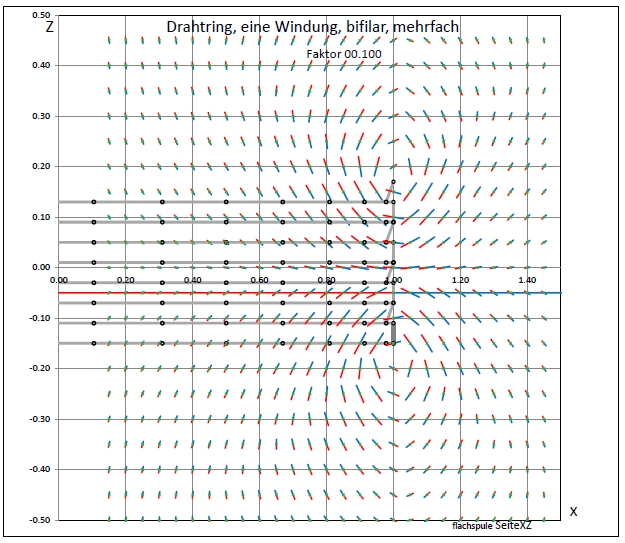Abb. 02-02-04: vier bifilare Ringe übereinander
    Bifilar = True
    offSetZ = 0.04
    posZ = -0.15
    MultiLayer = 3
    KopfText = " Drahtring, eine Windung, bifilar, mehrfach"
    Skalierung = 0.1
    DarStellung = 2 noch kleiner Schönheitsfehler beim Abstieg von einem Ring zum Nächsten. (FB)

3.1 Flachspule, einfach

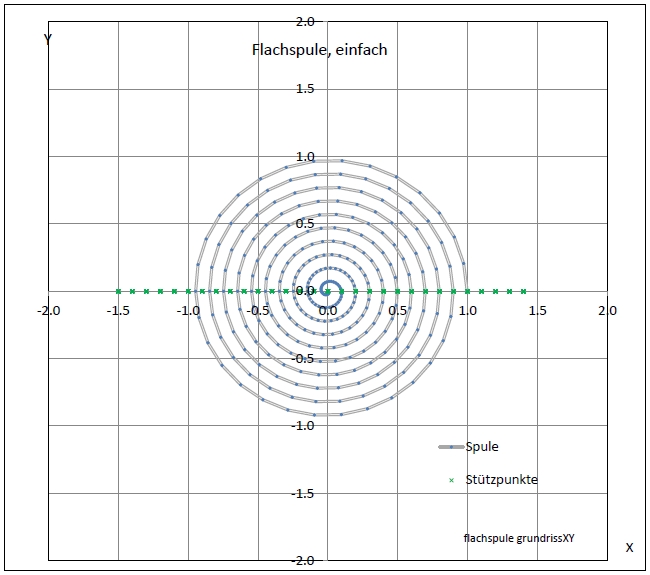Abb. 03-01-01: Der Strom fließt von außen nach innen. (FB)

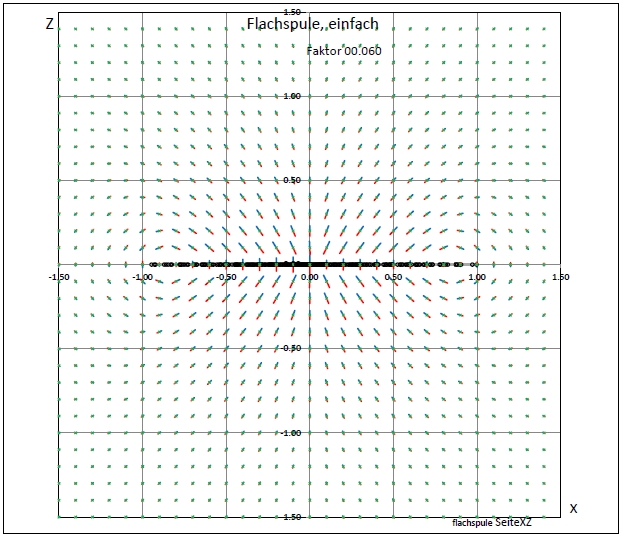Abb. 03-01-02: Auch hier bilden sich Wirbel um die Randbereiche herum. (FB)

3.2 Flachspule, bifilar

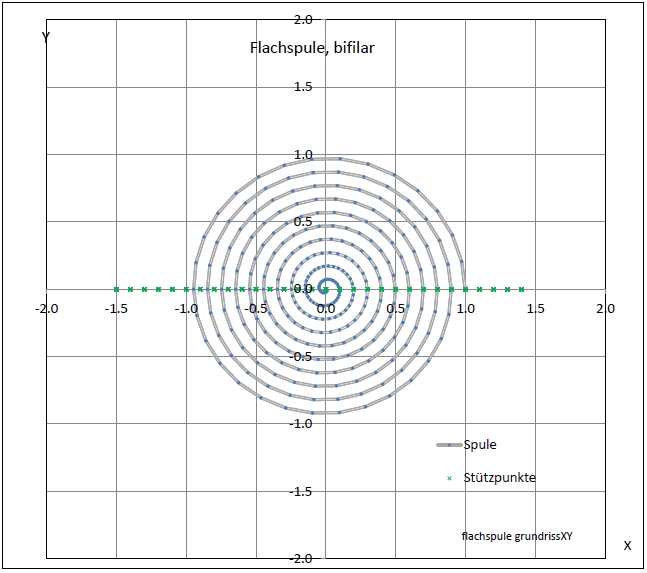Abb. 03-02-01: Der Strom fließt von außen durch die eine Spirale nach innen und von dort durch die andere wieder nach außen.

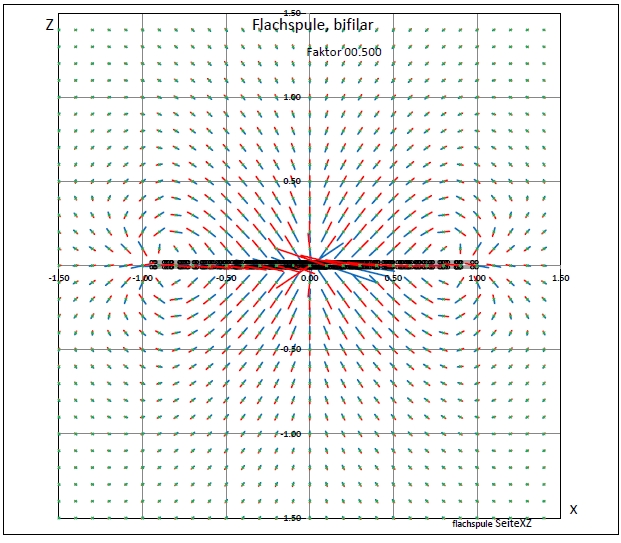Abb. 03-02-02: Zwei Flachspulen in geringen Abstand übereinander (FB)

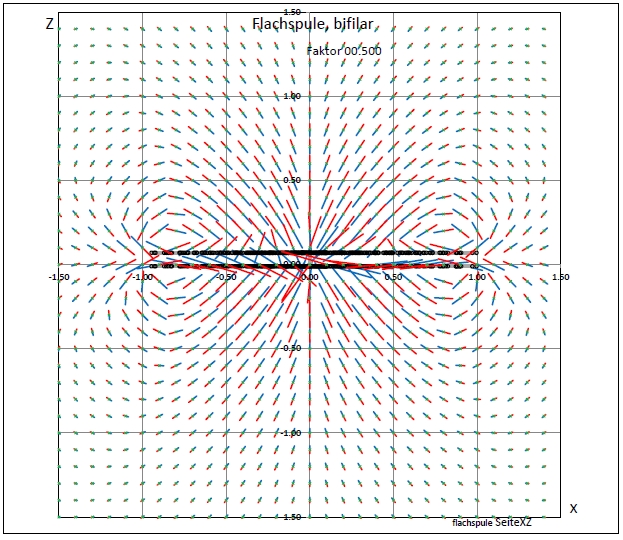Abb. 03-02-03: Zwei Flachspulen in größerem Abstand übereinander. (FB)

Abb. 03-02-04: Zoom: über und unter dem Rand gibt es Wirbel (FB)

4. Flachspule bifilar, als YinYang-Spule

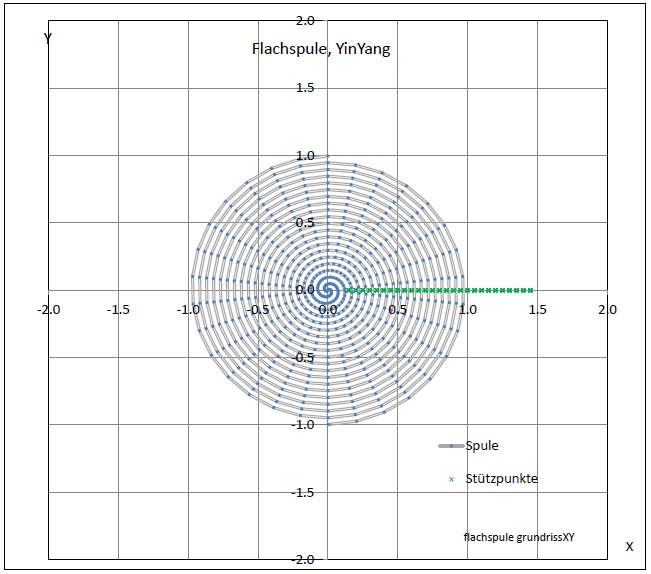Abb. 04-01: Zwei Flachspulen in der Mitte verbunden und gegeneinander um 180° gedreht.
Der Strom fließt über die eine Spule von außen nach innen und über die andere wieder nach außen. (FB)

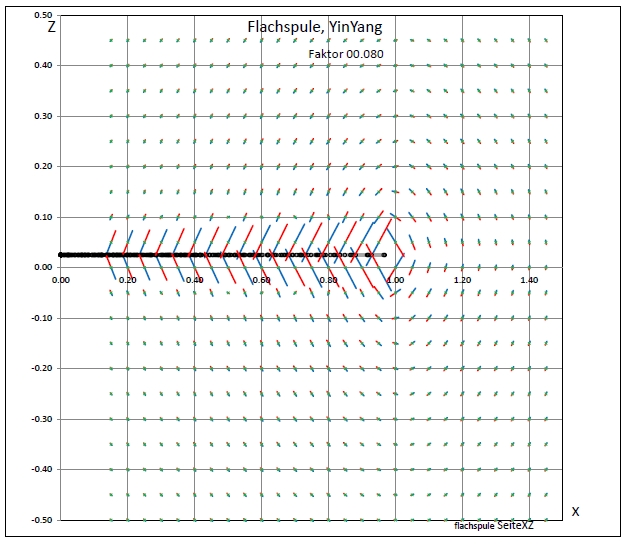Abb. 04-02: Wirbel um den Rand herum, große Feldänderungen zwischen den Drähten. (FB)

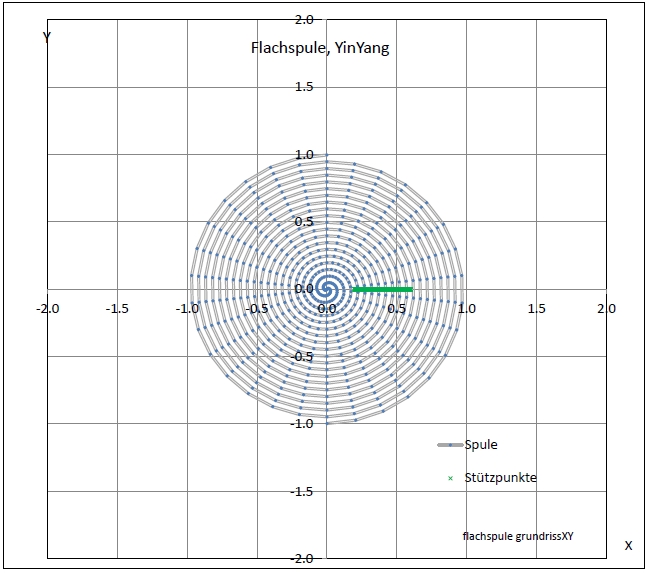Abb. 04-03: Nahbereich (FB)

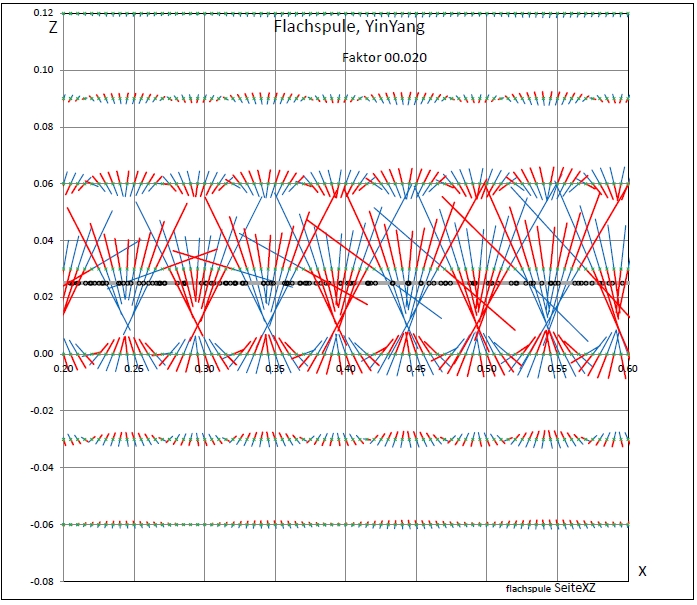Abb. 04-04: Wellenförmige Ausrichtung über den einzelnen Windungen (FB)

5. Rechenprogramm

' alle Positionen auswerten nach Biot-Savart

(Wikipedia http://de.wikipedia.org/wiki/Biot-Savart-Gesetz)

Statt Integral wird diskret aufsummiert.
Die Konstanten vor dL werden als 1 angenommen.

Basic-Programm
(F. Balck)

'***********************************************************
For m = 1 To mMagn ' Über alle Stützpunkte
    MagnIntensX(m) = 0
    MagnIntensY(m) = 0
    MagnIntensZ(m) = 0

' ********************************************
      For n = 1 To nSpule - 1 'über alle Spulenpunkte - 1 ( einer weniger für die Differenz)
' Mitte eines Elementes auf der Spule
        X0 = (SpulePosX(n + 1) + SpulePosX(n)) / 2
        Y0 = (SpulePosY(n + 1) + SpulePosY(n)) / 2
        Z0 = (SpulePosZ(n + 1) + SpulePosZ(n)) / 2

' vektor vom Stützpunkt für das zu berechnende Feld zum Spulenpunkt   r - r'
       X2 = MagnPosX(m) - X0
       Y2 = MagnPosY(m) - Y0
       Z2 = MagnPosZ(m) - Z0

' Abstand zwischen dem Stützpunkt und der Mitte des Spulenelementes | r-r' |
        Abstand = Sqr(X2 ^ 2 + Y2 ^ 2 + Z2 ^ 2)

' Vektor eines Elementes auf der Spule     dL
        X1 = SpulePosX(n + 1) - SpulePosX(n)
        Y1 = SpulePosY(n + 1) - SpulePosY(n)
        Z1 = SpulePosZ(n + 1) - SpulePosZ(n)

'Kreuzprodukt xyz(1) x xyz(2) dividiert durch Abstand^3 (Biot-Savart) dl x r-r'

        X =   (Y1 * Z2 - Z1 * Y2) / Abstand ^ 3
        Y = -(X1 * Z2 - Z1 * X2) / Abstand ^ 3
        Z = (X1 * Y2 - X2 * Y1) / Abstand ^ 3
' aufsummieren Biot-Savart
        MagnIntensX(m) = MagnIntensX(m) + X
        MagnIntensY(m) = MagnIntensY(m) + Y
        MagnIntensZ(m) = MagnIntensZ(m) + Z

      Next n
   '*********************************************************
   'normieren durch Anzahl der Spulenelemente
    MagnIntensX(m) = MagnIntensX(m) / (nSpule - 1)
    MagnIntensY(m) = MagnIntensY(m) / (nSpule - 1)
    MagnIntensZ(m) = MagnIntensZ(m) / (nSpule - 1)
Next m

'Skalierung und Komprimierung der MagnetfeldIntensität durch zweite Wurzel

' für die Berechnung der Fähnchen
    aX = MagnIntensX(m)
    b = Sgn(aX)
    aX = b * Skalierung * (Abs(aX)) ^ 0.5
'ax = MagnIntensX(m) * Skalierung

    aY = MagnIntensY(m)
    b = Sgn(aY)
    aY = b * Skalierung * (Abs(aY)) ^ 0.5
'ay = MagnIntensY(m) * Skalierung

    aZ = MagnIntensZ(m)
    b = Sgn(aZ)
    aZ = b * Skalierung * (Abs(aZ)) ^ 0.5
'az = MagnIntensZ(m) * Skalierung

' für die rechten Spalten in der Tabelle
    MagnIntensX(m) = SkalierungZwei * MagnIntensX(m)
    MagnIntensY(m) = SkalierungZwei * MagnIntensY(m)
    MagnIntensZ(m) = SkalierungZwei * MagnIntensZ(m)

Literatur: b-literatur.htm