Friedrich Balck > Vermessung > Daten

Vermessungen in Archäologie und Denkmalpflege

1. 2D- und 3D-Vermessung

2. Domvohalle in Goslar
3.----

4. Feuergezäher Gewölbe Weltkulturerbe Rammelsberg in Goslar

5. Aufwältigung und Neubau des Kanekuhler Kehrrades im Rammelsberg

6. Sakristei in der Alexanderkirche in Wildeshausen

Literatur:

Friedrich BALCK und Lothar KLAPPAUF,
Trigomat - ein universelles Vermessungssystem für die zeichnerische Dokumentation in der Denkmalpflege, Schriftenreihe des Deutschen Nationalkomitees für Denkmalschutz, Band 44, Seite 123-128 (1992)

Friedrich BALCK,
Computergestützte Vermessung der Domvorhalle in Goslar, Ordo et Mensura V, Sachüberlieferung und Geschichte, Siegener Abhandlungen zur Entwicklung der materiellen Kultur, Bd. 25, S.329-340, hrsg. Dieter Ahrens und Rolf C.A. Rottländer, Scripta Mercaturae Verlag, St. Katharinen 1998, ISBN 3-89590-052-4 (Abbildungen fehlen) domvorhalle.pdf

Friedrich BALCK,
Materialsammlung zur virtuellen Rekonstruktion, Stiftskirche St. Simon und Judas (Goslarer Dom),
Verlag Fingerhut, Clausthal-Zellerfeld, 2001, ISBN 3-935833-00-8, 132 Seiten, 260 Farbbilder
2. Auflage Papierflieger Verlag, Clausthal-Zellerfeld, 2016, ISBN 978-3-86948-412-9
DOI: 10.21268/20140612-234044 (http://dx.doi.org/10.21268/20140612-234044)

0. Vorgängerversionen für 2D-Dokumentation

Abb. 00-01: Pantograph, Eichstädt, erlaubt 2D-Dokumentation,
umgerüstet mit Meßaufnehmer zum Anschluß an TRIGOMAT-Programm (FB)

ABb. 00-02: Kartomat, große Version, erlaubt 2D-Dokumentation
Für die Ausgrabung der Heuneburg entwickelt http://www.heuneburg.de/ (FB)

Abb. 00-03: Kartomat, kleine Version, umgerüstbar mit Meßaufnehmern für TRIGOMAT-Programm (FB)

https://www.b-f-k.de/webpub01/pdf/bfk-erfassung-von-kulturguetern.pdf

https://www.b-f-k.de/webpub01/cnt/wanke.htm

Ein Vergleich verschiedener Aufnahmemethoden für die Archäologische Dokumentation
Von Tilman Wanke, Dipl. Ing. (FH)

Ein sehr gutes Ergebnis bei der steingerechten Maueraufnahme lieferte das Trigomatsystem: Bei der geringsten Arbeitszeit lag die Genauigkeit nur knapp hinter der des Tachymeters. Allerdings ist die erzielbare Darstellung als digitaler Vektorplan nicht so detailliert wie eine überarbeitete Pantografaufnahme. Systemeigene Messfehler sind bei diesem Gerät minimal. Die größten Abweichungen dürften auch hier durch Lotungsfehler und unsauberes Abgreifen der Messpunkte entstehen. Leider wurde das DOS-basierte Trigomatprogramm zu einem Opfer der Softwareentwicklung: Ab Windows XP läuft es aufgrund von Problemen mit der seriellen Schnittstelle nicht mehr. Eine marktfähige Windowsversion ist nicht in Aussicht. Gegen die Verwendung auf älteren Betriebssystemen spricht jedoch nichts, solange die Geräte noch vorhanden sind. Die Ausgabe der kodierten Messdaten in DXF-Format für eine Weiterverarbeitung und Speicherung in CAD ist problemlos möglich.

1. 2D- und 3D-Vermessung

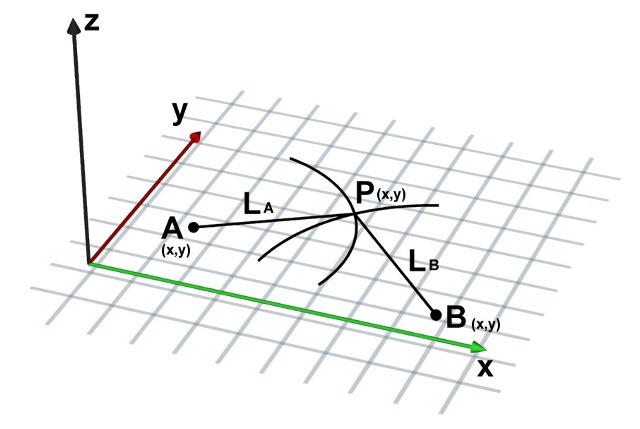Abb. 01-01: Zweidimensionaler Bogenschlag,
es gibt zwei Stativpunkte A und B bei der 2D-Version
Aus den Längen L_A und L_B läßt sich bei bekannten Positionen A und B die Position von P ermitteln. (FB)

Abb. 01-02: Dreidimensionaler Bogenschlag,
es gibt drei Stativpunkte A, B und C bei der 3D-Version.

Aus den Längen L_A, L_B und L_C läßt sich bei bekannten Positionen A, B und C die Position von P ermitteln.

Wichtige Eigenschaften des TRIGOMAT-Programms:

Bei beiden Versionen gibt es jeweils zwei Lösungen +/-Wurzel(...) :
sie bedeuten oberhalb und unterhalb der Basislinie AB,
bzw. oberhalb oder unterhalb vom Dreieck ABC.
Über einen Software-Schalter läßt sich die richtige Lösung auswählen.
Intern arbeitet das Programm mit mathematisch günstigen Stativkoordinaten.
mit A (0, 0, Az); B (Bx, 0, Bz); C ( Cx, Cy, Cz)
Dann gibt es eine mathematisch geschlossene Lösung.
Die Höhen H_A, H_B, H_C (Az, Bz und Cz) sind mit einem Nivellier einfach zu bestimmen.
Die Abstände zwischen den Stativpunkten lassen sich mit Hilfe der Maßbänder per teach-in ermitteln.
Nach Eingabe der Koordinaten von zwei Paßpunkten P1 und P2 und dem Einmessen der beiden Positionen in den Systemkoordinaten werden mit Hilfe einer Transformation anschließend alle Meßpunkte in das jeweilige Weltsystem umgerechnet.
Die elektronisch ermittelten Meßlängen können durch "Zusatzlängen" (feste Werte) an die jeweiligen Zeiger-Bedingungen angepaßt werden.
Es gibt einen definierbaren Zusatz in Richtung der Z-Achse. (Verlängerung in Richtung der Schwerkraft)
Eine Verschiebung um feste Längen in allen drei Richtungen läßt sich per teach-in definieren.
Mit einem Plausibilitätstest kann die Gültigkeit der Einstellung getestet werden:
Man bringe den Meßpunkt P
bei 2D- in die Nähe der Basislinie AB und
bei 3D in die Verbindungsebene von ABC und
löse ein Maßband vom Verbindungsknoten. Dann suche man den Umschlagpunkt, bei dem eine Verkürzung dieses Bandes die Koordinatenbestimmung unmöglich macht (d.h. Anzeige eines mathematischen Fehlers).
Die Einstellung mit den Stativkoordinaten und Zusatzlängen ist dann plausibel, wenn der Umschlag schon nach wenigen Millimetern erfolgt. Erfolgt der Umschlag erst nach vielen Zentimetern oder überhaupt nicht, dann ist die Einstellung auf jeden Fall falsch und muß überarbeitet werden.

Mit einfacher Mathematik lassen sich aus den gemessenen Längen die Koordinaten errechnen.
Schon in der Programmversion von 1990 und mit den damals noch einfachsten Computern (IBM-286) folgte die Koordinatenanzeige in Echtzeit, d.h. simultan, der Bewegung des Knotenpunktes.

c**********************************
     2D- bogenschlag
c**********************************
c   b12 Länge der Basis A B
c   b13 Länge Punkt A bis P
c   b23 Länge Punkt B bis P
c   xb und yb Koordinaten von P

    xb=(b12**2-b23**2+b13**2)/ 2./ abs(b12)
    w= b13**2 - xb**2

    if (w .ge. 0.) then
        yb= sqrt(w)       ' zwei Lösungen oberhalb/unterhalb
        ireturn=0

c************************************************
    subroutine transform(cosphi,sinphi,x,y,xnull,ynull)
c************************************************
c Drehung um den Winkel phi und Verschiebung in der Ebene um xnull, ynull
    real    x,y,a,b,cosphi,sinphi,xnull,ynull
    a=x
    b=y
    x= a*cosphi -b*sinphi + xnull
    y= a*sinphi +b*cosphi + ynull

    return
    end

   3D-Bogenschlag
c**********************************
subroutine dreikugel(x2,y2,x3,R1,R2,R3,x,y,z,ierr)
c************************************************************
c   berechnet den Schnittpunkt x,y,z der drei Kugeln mit den Radien R1,R2,R3
c   Kugel 1 liegt im Nullpunkt bei   A   bei 0, 0
c   Kugel 2 liegt in der xy-Ebene   C bei x2,y2
c   Kugel 3 liegt auf der X-Achse B bei x3, 0
c   wenn ierr=1, dann Fehler
c
    integer ierr
    real    x2,x3,a
    real    r1,r2,r3

    ierr=1
    if (y2.eq.0) return
    x = ( x3*x3 - r3*r3 + r1*r1 ) / (2*x3)
    y = (-2*x*x2 + x2*x2 + y2*y2 + r1*r1 - r2*r2 )/(2*y2)
    a=( r1*r1 - x*x - y*y )
    if (a.ge.0.)then
        z = sqrt(a)   ' zwei Lösungen oberhalb/unterhalb
        ierr=0
    endif
    return
    end
(FB)

Abb. 01-03: 2D-Trigomat, Maßbandsystem, computergestützte Vermessung
Schnittpunkt von Kreisbögen um feste Punkte.

bei 2D: Schnittpunkt von zwei Kreisen
bei 3D: Schnittpunkt von drei Kreisen

Hier sind es zwei elektronisch auslesbare Maßbänder mit Federrückzug, die sich auf einem Zapfen im Boden drehen können. (Stativpunkt).
Der Computer kennt die Längen jeweils vom Stativpunkt bis zum Verbindungspunkt (mit den Ring und den beiden Karabinerhaken) und errechnet daraus dessen Koordinate.
(FB)

Abb. 01-04: elektronisches Maßband, mit gestanzten Löchern,
links am Bildrand die Spule für das Maßband mit Federrückzug (Zubehör für Rolläden), Stachelwalze mit Inkrementalgeber und nach rechts folgt die Umlenkrolle, am Maßband-Anfang ist ein Karabinerhaken.
Der Drehpunkt ist eine Bohrung im Aluminiumklotz hinter der Umlenkrolle. (FB)

Abb. 01-05: zweidimensionaler Bogenschlag. Faktor für Fehlerfortpflanzung.
Ein Fehler bei einem Maßband von 1 mm erzeugt innerhalb des Quadrates einen Fehler von 2,5 mm bei den Koordinaten. Auf der Verbindungslinie zwischen den beiden Stativpunkten A und B kann der Faktor sehr groß werden. Solche Meßpositionen mit "schleifenden Schnitten" sind zu vermeiden. (FB)

Abb. 01-06: Drehpunkt zur Aufnahme der Maßbänder, 10 mm Gewindeschraube (FB)

Abb. 01-07: Drehpunkt, Grundplatte mit Blei beschwert (FB)

Abb. 01-08: 2D-Vermessung, zwei Zahnriemen mit Federrückzug und elektronischem Aufnehmer, der Computer kennt jeweils die Längen bis zum Verbindungspunkt (zwischen den Fingern des Autors). (FB)

Abb. 01-09: Bogenschlag um drei feste Punkte, Schnittpunkt von drei Kreisen.
3D-Vermessung mit tragbarem Computer, IBM-PC 286-Serie
Der Computer kennt die Länge der drei grünen Seile (Zahnriemen) vom jeweiligen Stativpunkt bis zum Verbindungsknoten mit den drei Karabinerhaken. Die herunterhängende Stange dient zum Anzeigen von Objekten, die mit dem Knoten nicht direkt zugänglich sind.
(FB)

Abb. 01-10: Prototyp, ganz am Anfang, 3D-Vermessung, Verlängerung des Knotens nach unten mit einer Stange (FB)

Abb. 01-11: Der Archäologe Dr. Lothar Klappauf bei den ersten Testmessungen (FB)

Abb. 01-12: 3D-Trigomat, computergestützte Dokumentation auf einer Grabung. 9.11.1994 (HB)

Abb. 01-13: Meßspitze mit drei Seilen und Metalldraht zu deren Schutz (FB)

Abb. 01-14: Meßspitze mit drei Seilen, die Lochung der Bänder ist gut zu sehen. (FB)

Abb. 01-15: Meßspitze mit Kugelhalterung. Die Schwerkraft hält den Zeiger (eine Gewindestange) senkrecht. Das Gewinde ist leicht mit Zusätzen zu verlängern. (FB)

Abb. 01-16: Meßspitze verlängert mit Gewindestange und Gewicht (der Autor bei der Arbeit). (FB)

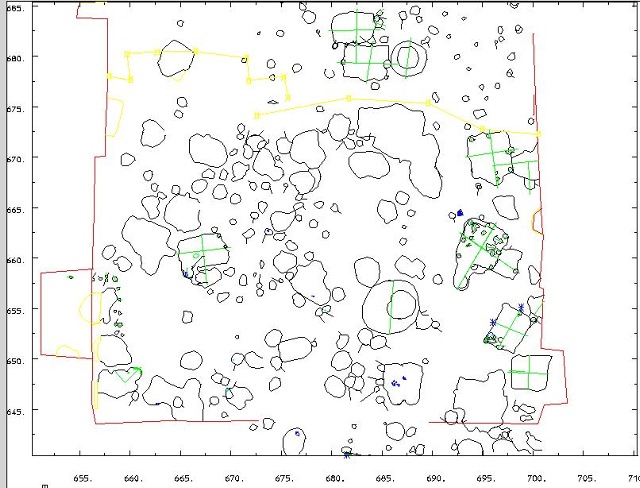Abb. 01-16a: Steine, (Aufmaß mit Tachymeter), die Funde sind farblich kodiert. (FB)

Abb. 01-17: Meßspitze aus Drahtlitzen, mit einer Stange aus dem Gartencenter lassen sich auch höhere oder tiefere Objekte antasten (FB)

Abb. 01-18: 3D-Trigomat, Verländerung der Meßspitze nach unten mit einem gekröpften Zeiger.
Die Libelle am Handgriff ermöglicht senkrechte Peilung nach unten (FB)

Abb. 01-19: gekröpfte 2D-Tastspitze, damit erreicht man auch unzugängliche Positionen.
Die Unterlage sorgt für eine parallele Führung.
grüner Zahnriemen, elektronischer Drehgeber mit Zahnrad und Federrückzug im braunen Gehäuse (FB)

Abb.01-20: 2D-Tastspitze. Als Zusatzlängen und Karabinerhaken dienen Teile aus dem Anglerbedarf. (FB)

Abb. 01-21: Drei Stative, Knotenpunkt in der Mitte. Die Eimer sind als Beschwerung mit Sand/Steinen gefüllt. (FB)

Abb. 01-22: drei Stative mit Eimern (Steine, Sand) beschwert. (FB)

Abb. 01-23: 3D- Vermessung einer Malerei auf Steinen in Costa Rica, die
Stative sind aus Baumstämmen. (K-U. V.)

Abb. 01-24: Friedhof, Kloster hinter den Brüdern in Goslar (FB)

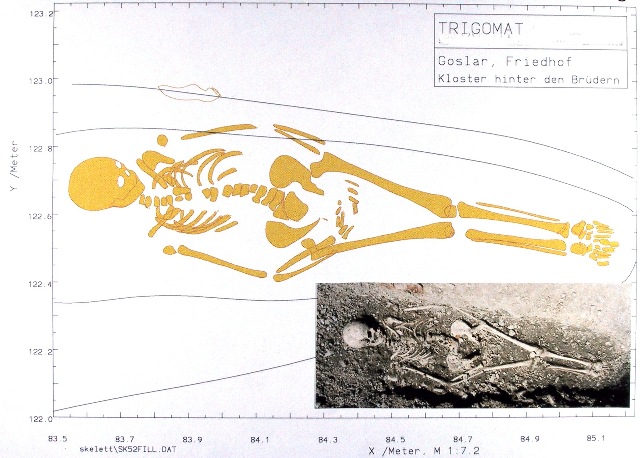Abb. 01-25: Skelett (FB)

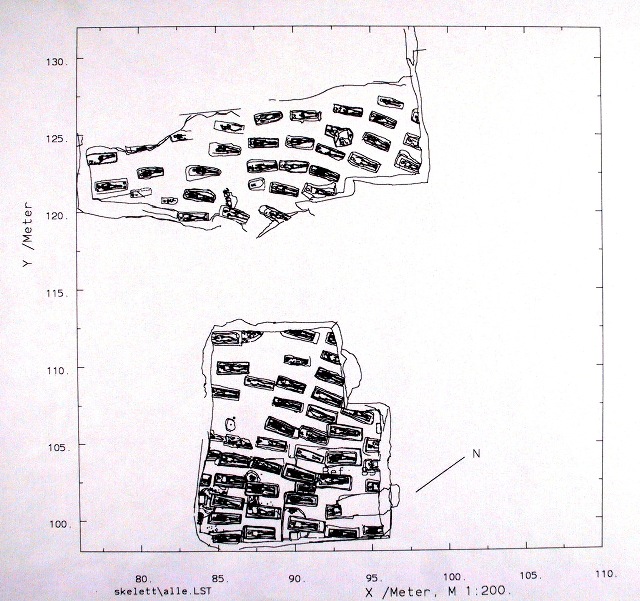Abb. 01-26: Gesamtplan, Kloster hinter den Brüdern (FB)

Abb. 01-27: 3D-Vermessung, ortsfeste Stative erlauben schnellen Aufbau (FB)

Abb. 01-28: Ortsfestes Stativ (FB)

Abb. 01-29: Maßbänder mit Regenschutzhaube /Transportkiste (FB)

Abb. 01-30: ein Brunnen (FB)

Abb. 01-31: der Brunnen, das Ergebnis (FB)

Abb. 01-32 schnell aufgebaut, Grabung in Nienover, Eimer mit Steinen zum Fixieren der Stative (FB)

Abb. 01-32a: Grabung in Nienover (FB)

Abb. 01-32b: Handgerät für die Datenerfassung und Bedienung des Programms, Grabung in Nienover (FB)

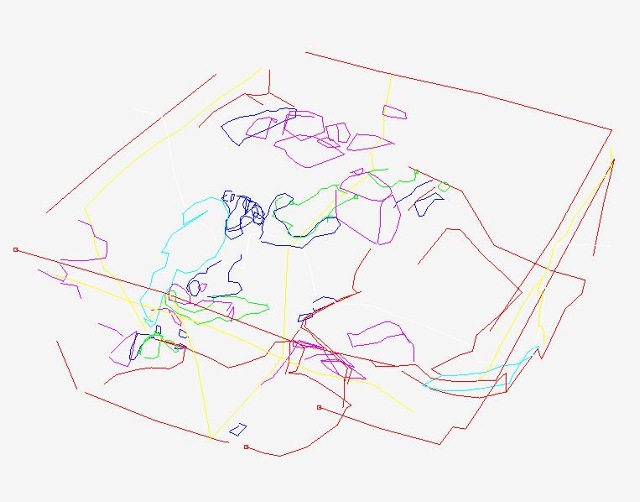Abb. 01-32c: Grabung in Nienover, Schrägansicht, farbliche Codierung der unterschiedlichen Linientypen
3D- Daten als .IGS ofen319a.igs und als .DXF ofen319a.dxf
(FB)

Abb. 01-33: in der Lichtensteinhöhle (FB)

Abb. 01-34: Johanniskirche, Ruine, Magdeburg, Meßspitze mit Verländerung. (FB)

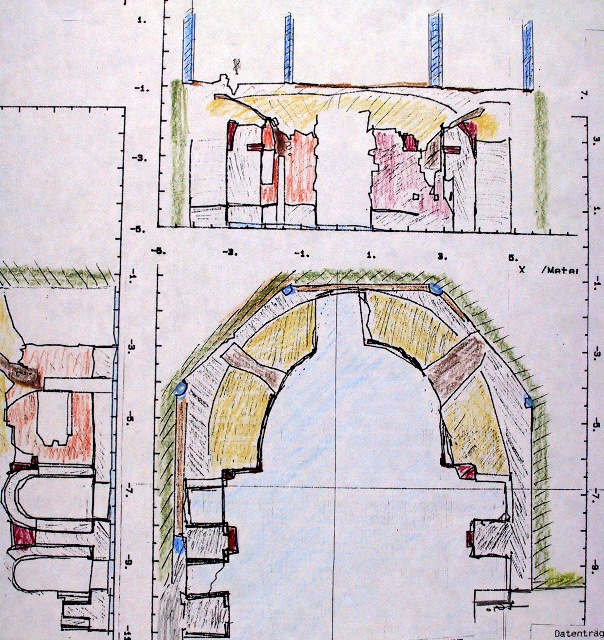Abb. 01-35: Daten der Johanniskirche, kompletter Datensatz der 3D-Vermessung. (FB)

Abb. 01-36: Einsatz im Waggonbau für Container. Die Seile werden von einem Motorsystem gespannt. Stivpunkte auf der blauen Säule und rechts an der Kranbahn.
Nach der Messung sind die Seile schnell wieder aus dem Arbeitsbereich entfernt.(FB)

Abb. 01-37: Meßpositionen bei einem Container-Waggon (FB)

Abb. 01-38: Römisches Schiff von Unterstimm (FB)

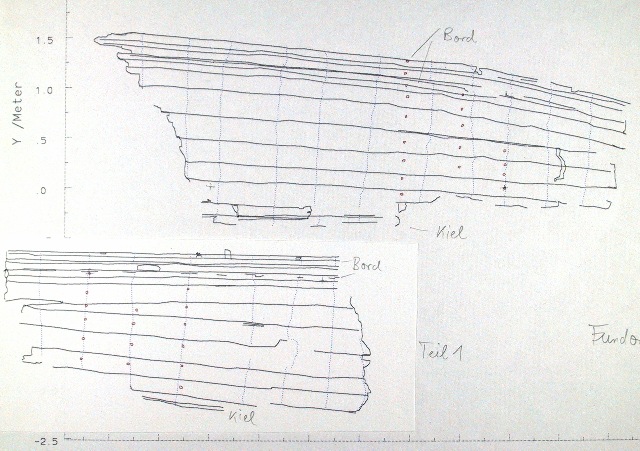Abb. 01-39: Ergebnis der Vermessung: Römisches Schiff von Unterstimm (FB)

Abb. 01-40: kleine Version für die Restaurierungswerkstatt, z. B. für eine Blockbergung (FB)

Abb. 01-41: in der Werkstatt (FB)

Abb. 01-42: kompliziertes Objekt, der Halter erlaubt das Umklappen um 180°, so daß Ober- und Unterseite im gleichen Koordinatensatz gemessen werden können. (FB)

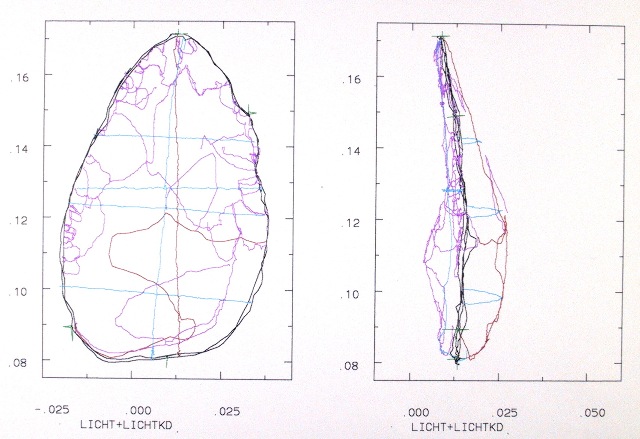Abb. 01-43: Ergebnis (FB)

Abb. 01-44: feines und kleines Objekt, Vermessung in 3D (FB)

Abb. 01-45: Unterwassertauglich (FB)

Abb. 01-46: unter Wasser (FB)

Abb. 01-47: Test im Flachwasser, das Boot muß gut verankert sein (FB)

Abb. 01-48: Eigenbau: Laserentfernungsmesser gekoppelt mit russischem Theodolit

DISTTHEO.SP5          23.09.1995    19:01:25;11
Disto mit zwei Drehgebern    und THEO, Horizontal gleich NULL
    Messung ab Vorderkante

(FB)

Abb. 01-49: einige Jahre später (FB)

2. Domvorhalle in Goslar

Vermessung mit elektrooptischem Entferungsmesser DISTO, Theodolit sowie 2D-Maßbandsystem TRIGOMAT Februar 1995

Datensatz < 1 MB im Format IGES dom-dalles.igs
von gängigen CAD-Programmen zu öffnen.
https://de.wikipedia.org/wiki/Initial_Graphics_Exchange_Specification

ZEIT12.02.1995    09:44:23--DOMHALLE\094423.U12
KOPF12.02.1995    09:44:23
KOPFDomhalle goslar, Fassade ( .sp5)
KOPF                  mit dist0
ZEIT12.02.1995    09:44:23
GRUND1 2.3650, -4.5476, 1.5600, 2.6865, -5.4946,   .0000,   .0000, 1.0000,
GRUND2   .0000, 4.6795, 3.6794,   .0000,   .0000, 4.0000,   .0000,
OFFSET         0.,        0.,        0.,
GRUND3   .0990, -.0220,   .0000,   .0000,   .0000,   .0000,   .0000,
GRUND5 4.0000, 3.9882,   .3356,   .3168,   .0000,   .0000,   .0118,
TYP 0 , Rand
up    1 FUND:0050 Farbe 001      oben 0!
    -4.7042,    -.0277,    2.8120,
    -4.7384,    -.0562,    3.7648,
    -4.8104,    -.0680,    3.8962,
    -4.8020,    -.0638,    3.9838,
    -4.7991,    -.0624,    3.9861,
    -4.7705,    -.0519,    4.1336,
    -4.1868,    -.0771,    4.5784,

DISTTHEO.SP5          23.09.1995    19:01:25;11
Disto mit zwei Drehgebern    und THEO, Horizontal gleich NULL
    Messung ab Vorderkante
   .0000, 90.0000,   .0000, ,Ausziehlaenge bei Init

Abb. 02-01: Rekonstruktion des Domes einschließlich der Vorhalle. (Henning Balck)

Abb. 02-01a: Rekonstruktion (Henning Balck)

Abb. 02-01b: Das Original, vom Parkplatz aus fotografiert. (FB)

Abb. 02-02: im Hintergrund die Kaiserpfalz (FB)

Abb. 02-03:

Abb. 02-04: Die Vorhalle von der Straße aus. (FB)

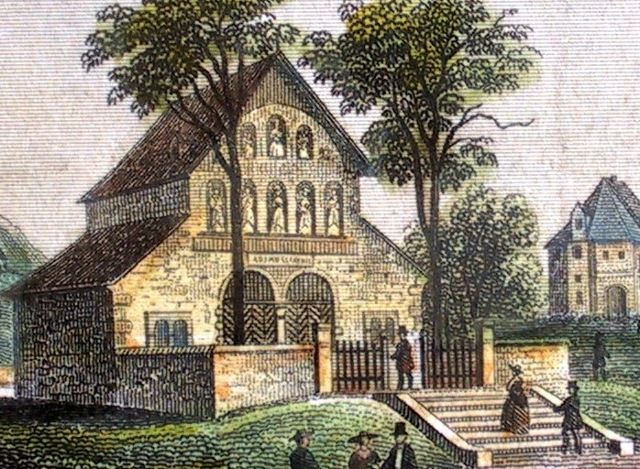Abb. 02-05: Die Vorhalle W. Ripe

Abb. 02-06: Der Kaiserstuhl (FB)

Abb. 02-07: Der Kaiserstuhl (FB)

Abb. 02-08: Der Kaiserstuhl (FB)

Abb. 02-09: (FB)

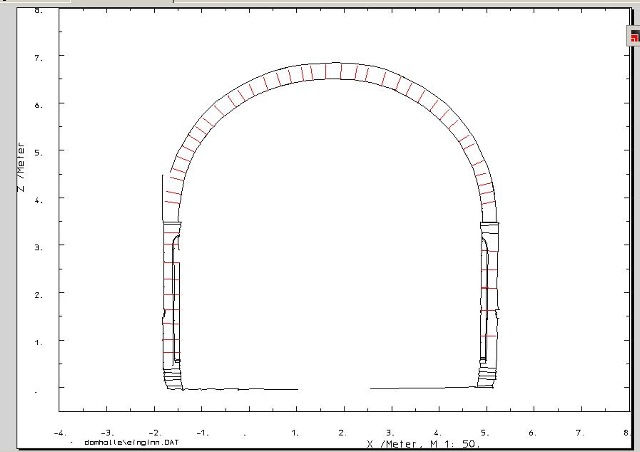Abb. 03-01: (FB)

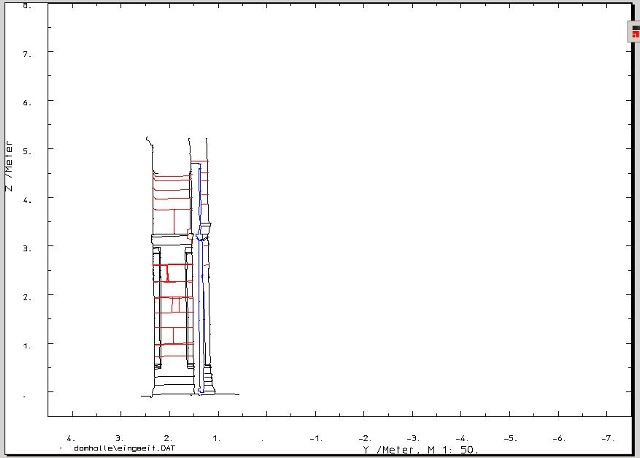Abb. 03-01a: 01.03.1995 (FB)

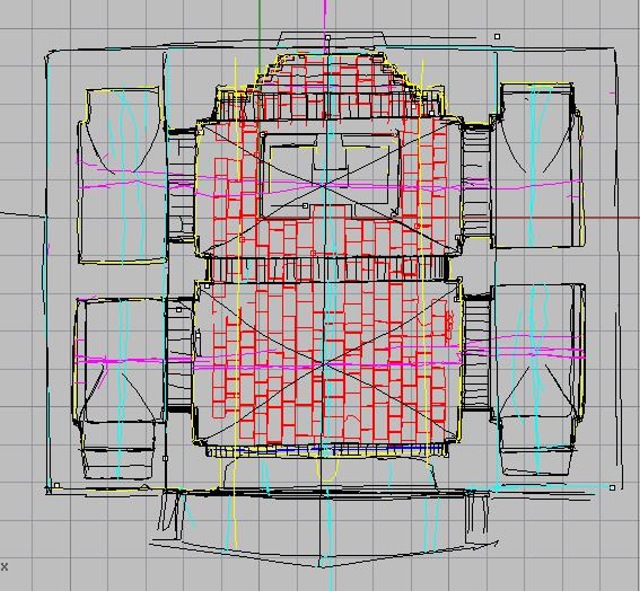Abb. 03-01b: Grundriß mit Raster, 1 Meter (FB)

Abb. 03-01c: (FB)

Abb. 03-02: (FB)

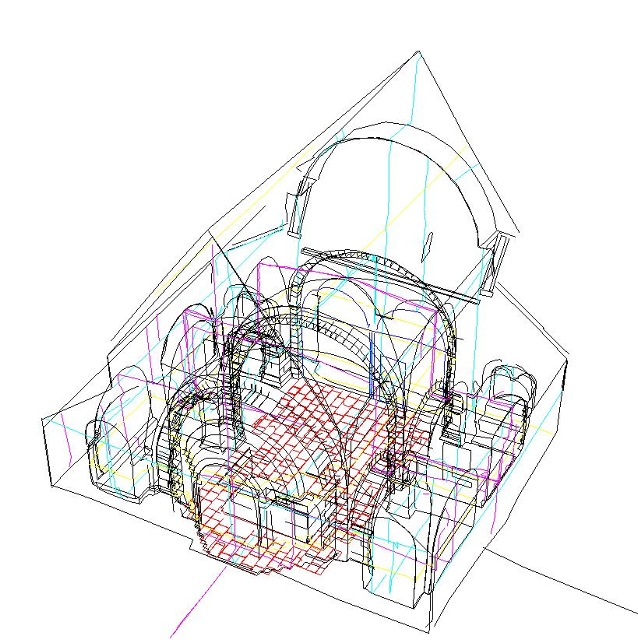
Abb. 03-04: (FB)

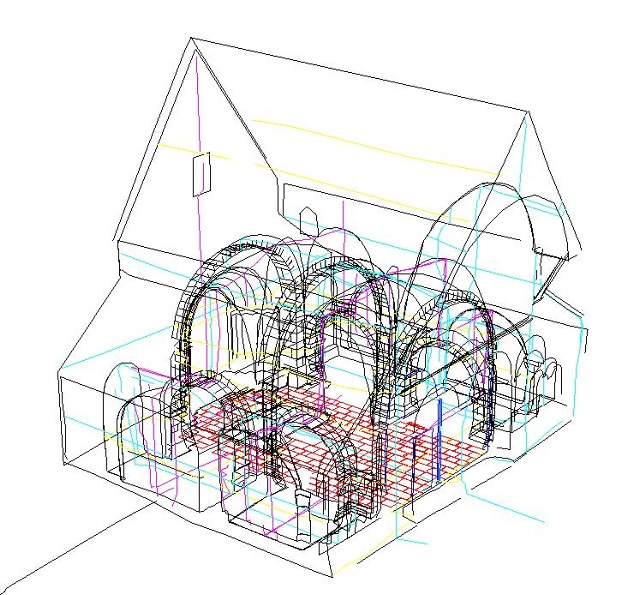
Abb. 03-05: (FB)

Abb. 03-06: (FB)

4. Feuergezäher Gewölbe Weltkulturerbe Rammelsberg in Goslar

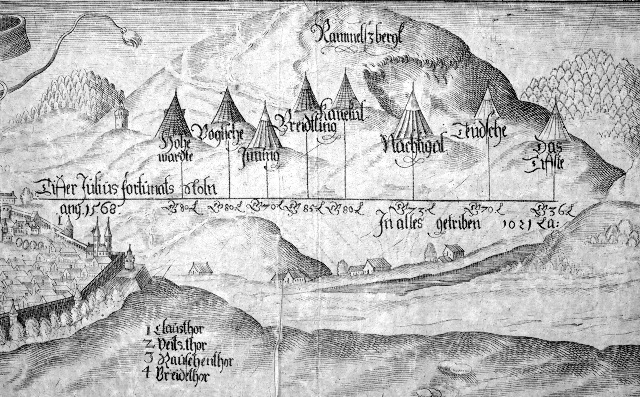Abb. 04-01:
Die Gruben am Rammelsberg mit Julius-Fortunatus-Stollen (Koch / Lindemeir 1606)

Abb. 04-02: Rammelsberg, Modell mit altem (Mitte) und neuem (rechts) Lager,
Oskar Langer, 1950 (FB)

Abb. 04-03: Das Feuergezäher Gewölbe ist unten in der Mitte, das Kanekuhler Kehrrad oben rechts. (FB)

Aus der Habilitationsschrift es Autors:

Friedrich BALCK,
Wasserkraftmaschinen für den Bergbau im Harz, Frühneuzeitliche Spuren und deren Bedeutung am Beispiel der Grube Thurm Rosenhof und ausgewählter Anlagen, 277 S., 147 Abb., Clausthal-Zellerfeld: Papierflieger, 1999, ISBN 3-89720-341-3 ( in geringer Auflösung: balhabil-lowdens.pdf)

4.2.14.1 Feuergezäher Gewölbe im Rammelsberg, Goslar, (Nr. 21)

Eine Fotoplatte, vermutlich aus der Zeit um die Jahrhundertwende, gewährt einen Einblick in das Feuergezäher Gewölbe zu der Zeit, als der Schacht unter dem Gewölbe noch offen war (Abb. 79). Bei Wilhelm Bornhardt [L54] findet sich eine ausführliche Abhandlung dieser Radstube mit beschreibendem Text sowie fünf Ansichten und einem Grundriß von Regierungsbaurat Becker, signiert mit 1930 ¹³¹. Das Gebäude ist nahezu vollständig ausgemauert.
An zwei verbliebenen Öffnungen in der Mauer (F), (H)– Abb. 81 steht noch der umgebende brüchige Schiefer, dessen Schichten unter 40° einfallen, an.
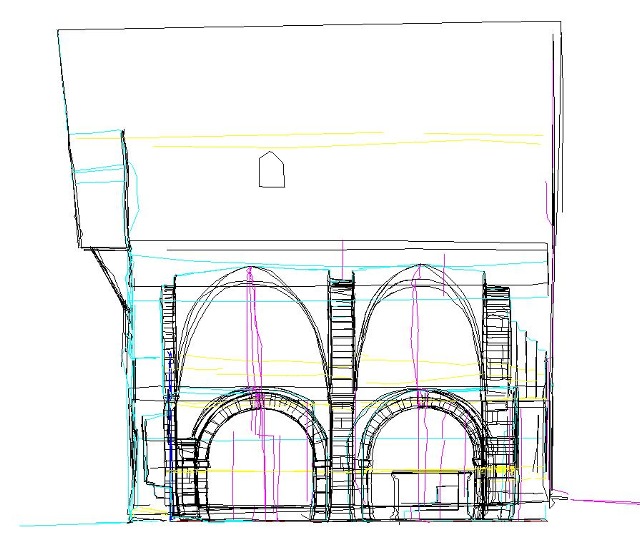
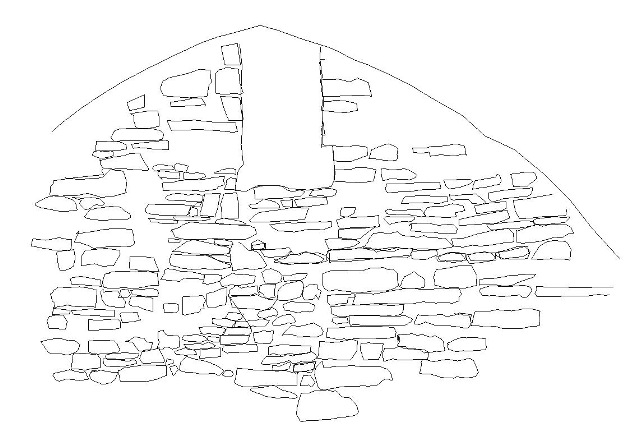
In Abb. 80 sind die Ergebnisse einer computergestützten geometrischen Vermessung von 1994 dargestellt. Es handelt sich um die Ansicht eines Drahtmodells⁹⁷. Alle gemessenen Linien sind gleichzeitig sichtbar. Für die Erfassung der Verformung wurden in nahezu regelmäßigen Abständen frei Hand Meßlinien auf die Wände gelegt, die hier gepunktet gezeichnet sind. Einen Ausschnitt mit steingerechtem Aufmaß gibt Abb. 81 wieder. Bei dieser Auflösung lassen sich die Maße und das Gefüge der Steine abgreifen. Einige der Steine im äußeren Bogen sind mehr als 70 cm lang. Die Seitenansicht 1 in Abb. 80 ist im Vergleich zu Abb. 81 und Abb. 82 seitenverkehrt, der Betrachter schaut durch eine »gläserne« SW-Wand.
Im Gegensatz zu der Zeichnung Beckers erlaubt der im Rechner gespeicherte Datensatz jederzeit die Abfrage von beispielsweise Differenzmaßen und Wandneigungen mit hoher Genauigkeit. Manche Idealisierungen, z. B. senkrechte Wände bei Becker, lassen sich mit den heutigen Daten vergleichen und anzweifeln.
Größere Veränderungen seit 1930, wie beispielsweise die eingebauten Stützkonstruktionen aus Holz und Eisen sowie der verschlossene Abgang in der SO-Stirnwand (E) fallen auf. Die ausgemauerte Nische in der SW–Wand mit den »Lampenöffnungen« (D) ist bei Becker noch nicht gemauert, er zeichnet dort natürliches Gestein. Kleinere Änderungen (Verformungen, Rißbildung) sind bei Becker nur mit Mühe zu erahnen.
Die reale Situation ergibt sich aus Abb. 82. Sie zeigt das »Gesicht« der Mauer mit unterschiedlichen Steinformen, Fugen und Füllmaterial sowie die Wand mit den Lampenöffnungen (D). Bei (C) tritt die starke Rißbildung im Gewölbebogen deutlich hervor. In der Nische (F) war nach Vorschlag von Bornhardt die Wasserradwelle gelagert. Er gibt den Durchmesser des Rades mit 6 m an. Diese Angabe kann stimmen, sie steht nicht im Widerspruch zur Geometrie des Raumes. Auch aus der Höhe der Nischen über dem Boden kann ein Radradius von 3 m abgeleitet werden. Da das Rad unsymmetrisch auf der dem Schacht abgewandten Seite (Richtung NO) der Welle steckte, brauchte man an der gegenüberliegenden SW-Längswand nicht soviel Freiraum zu schaffen. Somit wäre der trapezförmige Grundriß begründbar.
Neben der Aufnahme der exakten Geometrie wurden die Vermessungsarbeiten vor wenigen Jahren mit Schadensaufnahme¹³² und Beschreibung der Risse sowie kontinuierlichen Deformationsmessungen über einen längeren Zeitraum begleitet. Eine umfangreiche Fotodokumentation ist angelegt. Darüber hinaus wurden Präzisionsnivellierungen an speziell eingesetzten Meßbolzen durchgeführt, um Verformungen durch den Anstieg des Wassers im Grubengebäude nachzuweisen.

Dokumentation und Verformungsmessungen 1995 fgz2-word.pdf

Vermessung mit elektrooptischem Entferungsmesser DISTO, Theodolit sowie 2D-Maßbandsystem TRIGOMAT April 1995

Vermessungsdaten im IGES-Format
von gängigen CAD-Programmen zu öffnen.
https://de.wikipedia.org/wiki/Initial_Graphics_Exchange_Specification

erster-tag.igs
risse.igs
lampenwand.igs
suedost.igs
stirnwand.igs

Abb. 04-04: Historische Aufnahme um 1900

Abb. 04-05: Marken 1, 2
04.01.1995 (FB)

Abb. 04-06: Marke 2
rechts unten: der Rucksack des Autors (FB)

Abb. 04-07: Marken 3 und 4 (FB)

Abb. 04-08: Marke 5, die Lampenwand.
(die kleinen Öffnungen links und rechts sind nach 1930 entstanden) (FB)

Abb. 04-09: Marken 6 und 7
4.1.1995 (FB)

Abb. 04-10: Marke 7 (FB)

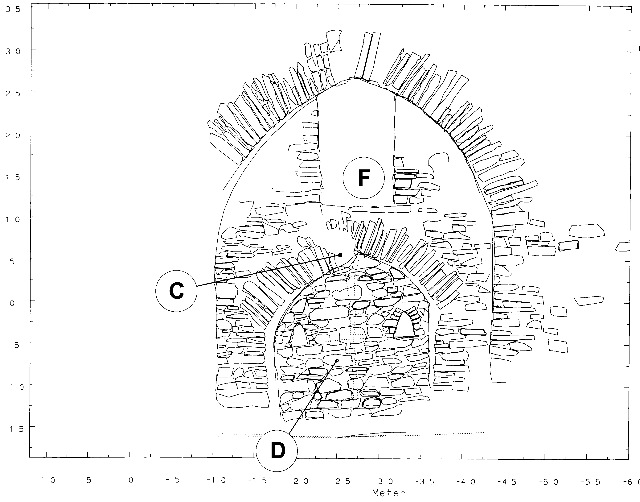Abb. 04-11: aus der Habil-Schrift (FB)

Abb. 04-12: aus der Habil-Schrift (FB)

Abb. 04-13: (FB)

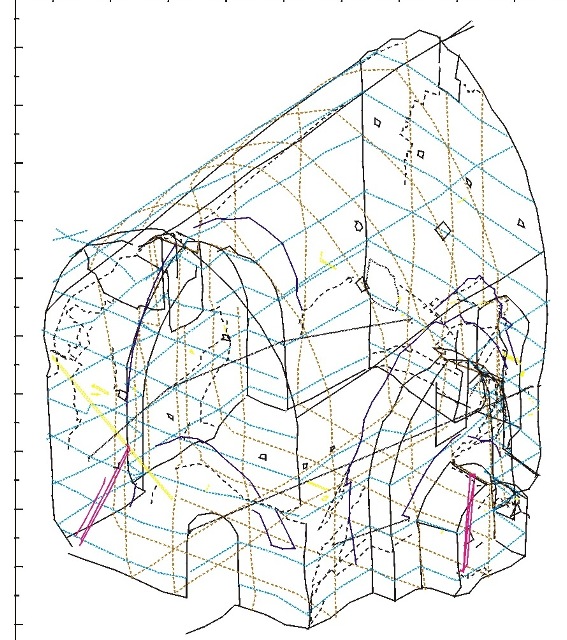Abb. 04-14: erster-tag.igs (FB)

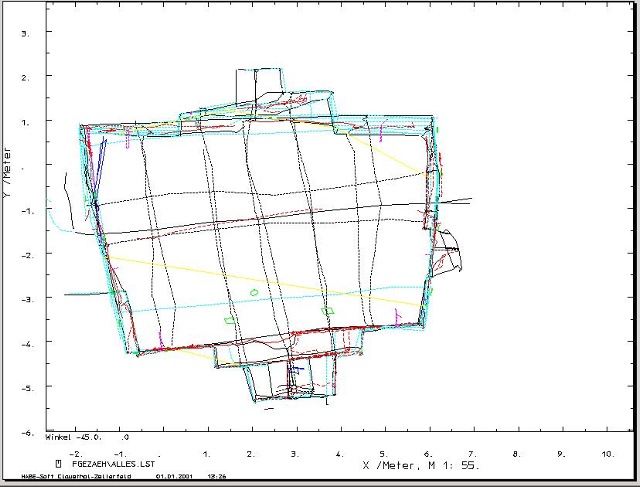Abb. 04-15: erster-tag.igs (FB)

Abb. 04-16: erster-tag.igs (FB)

Abb. 04-17: erster-tag.igs (FB)

Abb. 04-18: 2D- Datenaufnahme, steingerechtes Aufmaß der Süd-Ost-Wand. (FB)

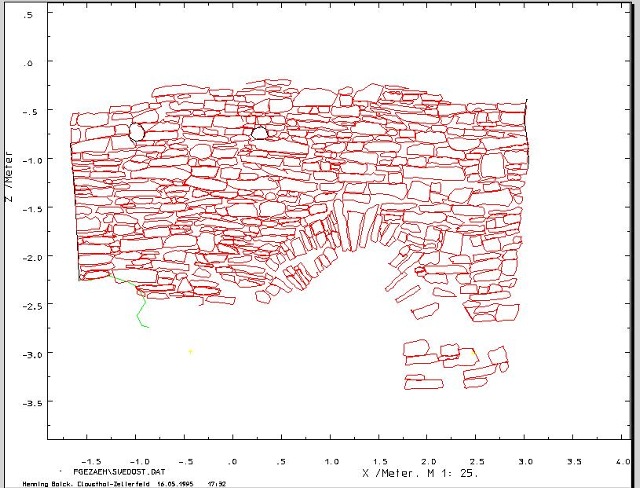Abb. 04-19: Suedost-Wand suedost.igs
(FB)

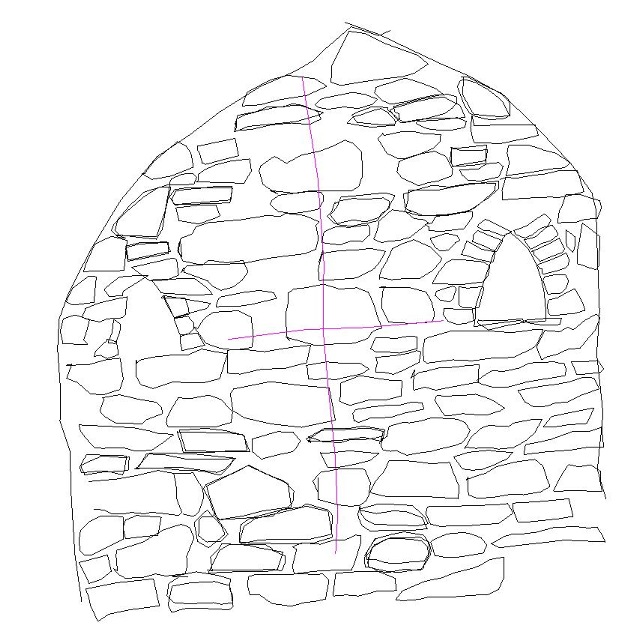
Abb. 04-20: Stirnwand stirnwand.igs
(FB)

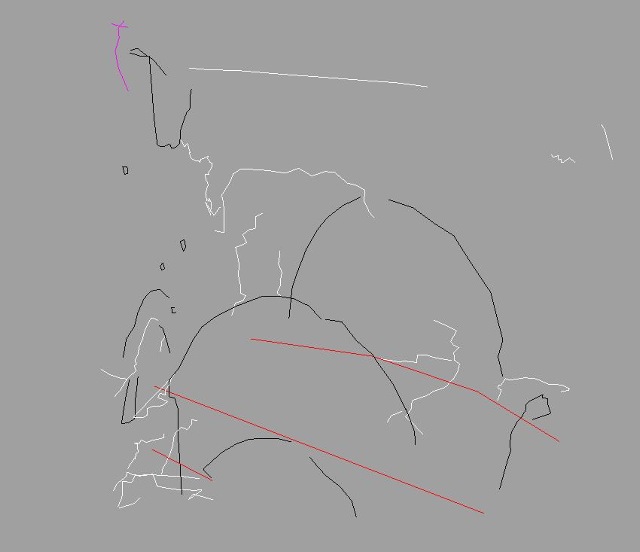
Abb. 04-21: Lampenwand lampenwand.igs
(FB)

Abb. 04-22: Risse. (weiß) risse.igs
(FB)

5. Aufwältigung und Neubau des Kanekuhler Kehrrades im Rammelsberg

Aus der Habilitationsschrift es Autors:

Friedrich BALCK,
Wasserkraftmaschinen für den Bergbau im Harz, Frühneuzeitliche Spuren und deren Bedeutung am Beispiel der Grube Thurm Rosenhof und ausgewählter Anlagen, 277 S., 147 Abb., Clausthal-Zellerfeld: Papierflieger, 1999, ISBN 3-89720-341-3 ( in geringer Auflösung: balhabil-lowdens.pdf)

4.2.14.2 Kanekuhler Radstube im Rammelsberg, Goslar, (Nr. 22)
In der von Roeder geplanten Kette erhält zuerst das Kehrrad des Kanekuhler Schachtes sein Wasser aus dem Herzberger Teich. Die Technik der Maschinenanlage entspricht mit ihrer Konstruktion der in der Ovalen Radstube am Thurm Rosenhof. Die Seilkorbwelle ist von der Radwelle getrennt und wird an jedem Ende über zwei Treibstangen durch das Wasserrad bewegt (vgl. Abb. 76). Diese stehen nicht senkrecht, sondern sind etwa 45° geneigt (Abb. 83). Der Abstand der beiden Wellen beträgt ca. 8,5 m.
Im Rahmen der Aufwältigungsarbeiten im Schleiftrog und für den Einbau von Besuchertreppen wurde die Geometrie dieser Radstube computergestützt vermessen.¹³³
In Abb. 84 sind die Daten für eine gefälligere Darstellung per Hand umgezeichnet. Bei (A) fließt das Wasser über den Roeder-Stollen heran, bei (B) verläßt es die Radstube. Für die Lager der schweren Wellen (C) gibt es vier gemauerte Fundamente. Der Schleiftrog ist wie bei der Runden Radstube am Thurm Rosenhof abgestuft. Das Bremsrad neben dem Wasserrad hat einen kleineren Durchmesser. Zum Transport des Baumaterials und als Zugang für die Wartung führt ein Abzweig vom Roeder-Stollen bis zur Kehrradwelle (D). Über einen kleinen Durchschlag auf der gegenüberliegenden Seite (E) gelangt man heute bis zu einer gut befahrbaren Strecke. Hier transportierte man 1995 das Material für das rekonstruierte Wasserrad bis zur Radstube.
Diese Querverbindung existierte noch nicht vor 1900, so daß man früher das gesamte Material über den mit Bohlen abgedeckten (Tretwerk) Roeder-Stollen hereinbringen mußte. Der Stollen bei (F) führt in Richtung Schacht.
Das erste Kehrrad wurde in dieser Radstube 1805 in Betrieb genommen. Bedingt durch den Verschleiß ersetzte man die Räder in größeren Zeitabständen (etwa 10–15 Jahre). Von einem Neubau 1882 existiert eine Aktennotiz [L4]:
»In der Woche vom 17.–24. Juni 1882 ist beim Kanekuhler Treibwerk ein neues, auf dem Werke von eigenen Leuten angefertigtes Kehrrad gehängt.«
Die entsprechende Angabe für das Jahr 1995 könnte etwa so lauten:
Nach einer Vorbereitung von etwa acht Wochen benötigten fünf Handwerker acht (lange) Arbeitstage, um die vorgefertigten Teile des rekonstruierten Kehrrades in die historische Radstube zu bringen und dort zusammenzubauen.
F. Balck und T. Ziegler [L23] haben über den Nachbau berichtet. Die Kosten für Material, Herstellung und Einbau (ohne Material für Doppelkrummzapfen) beliefen sich auf etwa 110.000 DM.
Eine weitere Aktennotiz spricht von einer Bremse an der Kanekuhler Fahrkunst:
»Eine Bremsvorrichtung für die Fahrkunst im Kanekuhler Schacht ist im laufenden Etatjahr eingebaut worden. 29. X. 01.«
In Abb. 86 hängt das neue Kehrrad fast fertig auf der Welle. Es muß nur noch ausgerichtet und mit der Welle verkeilt werden. Über die angelehnte Leiter gelangt man vom neuen Grundrahmen aus verzinktem Stahl (1) hinunter auf den oberen Absatz im Schleiftrog. Die Welle trägt ein hölzerner Lagerklotz (2) mit einer Lagerschale aus Bronze. Über die Bohlen (D) führt ein Weg nach links leicht ansteigend bis zum Roeder-Stollen hinauf.
Die letzten Meter bis zum Rad floß das Wasser aus dem Roeder-Stollen über ein hölzernes Gefluder. Hier konnte es bis zu einer gewissen Höhe angestaut werden. Als Abdichtung zwischen Gestein und Holz fand man 1995 eine Schicht aus Lehm.
Schräg über dem Kehrrad mauerte man zwei für die Lager der Seilkorbwelle steinerne Fundamente. In Verlängerung der Welle bieten auf jeder Seite zwei große Hohlräume viel Platz für die Kurbelzapfen.
Abb. 85 zeigt zwei dicke Balken, die auf dem Absatz im Schleiftrog liegen. Der kleinere Balken (1) gehört zum Grundrahmen, der größere (2) bildet mit den Schlitzen an jedem Ende die unteren Gelenke
((2)–Abb. 116) für die beiden senkrecht stehenden Bremsbäume¹³⁴. In der Ovalen Radstube ist der entsprechende Balken (N) geteilt). Zur Zeit der Aufnahme befand sich noch eine etwa 35 cm dicke Schlammschicht rechts neben den Balken mit Ablagerungen aus Zinksulfat (siehe Abschnitt Holzschutz 4.3.3. 2.2.13).

Daten im IGES-Format.
hoehle.igs

Mittlerweile ( 2020) ist der Neubau von 1995 wieder baufällig und muß ersetzt werden.

Abb. 05-01: das Chaos, Aufnahme der Positionen mit 3D-TRIGOMAT-System

Abb. 05-02: Der Knoten der drei Maßbänder ist die Meßspitze
Allle Fundstücke bekamen einen rotes Bändchen mit einer Nummer.
Die Ausgrabung erfolgte schichtweise: graben/ vermessen /graben usw. (FB)

Abb. 05-03: einer der drei Fixpunkte, an denen jeweils ein Maßbandsystem hängt. (FB)

Abb. 05-04: unten im Schleiftrog, der Platz für die Bremse. (FB)

Abb. 05-05: Die Welle aus Eiche, 60 cm x 60 cm (FB)

Abb. 05-06: Für die Besucher sichtbar: Blick auf die Form der Schaufeln. (FB)

Abb. 05-07: Gute Handwerksarbeit von http://www.muehlenbau-schumann.de/ (FB)

Abb. 05-08: Der Meister bei der Arbeit: Gottfried Schumann
http://www.muehlenbau-schumann.de/ (FB)

Abb. 05-09: Das neue Rad ist fertig. Der Autor mit gelbem Helm (FB)

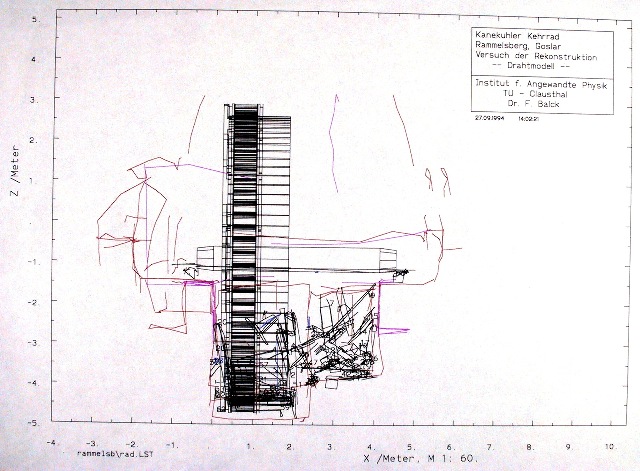Abb. 05-10: von der Seite: Fundstücke, Gebäude und Neukonstruktion (FB)

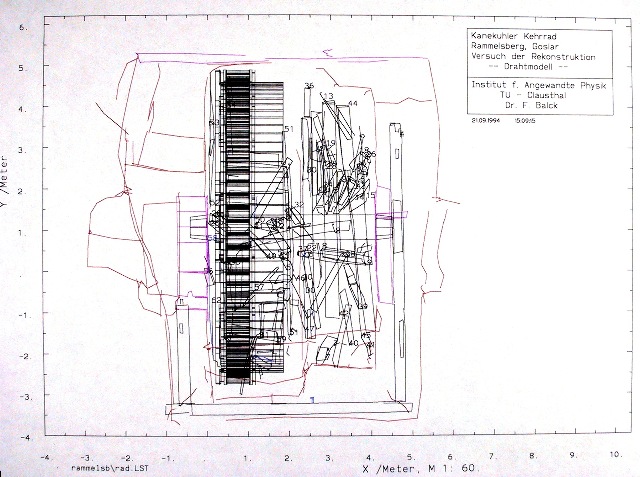Abb. 05-11: von oben: Fundstücke, Gebäude und Neukonstruktion (FB)

Abb. 05-12: von der Seite: Fundstücke, Gebäude und Neukonstruktion (FB)

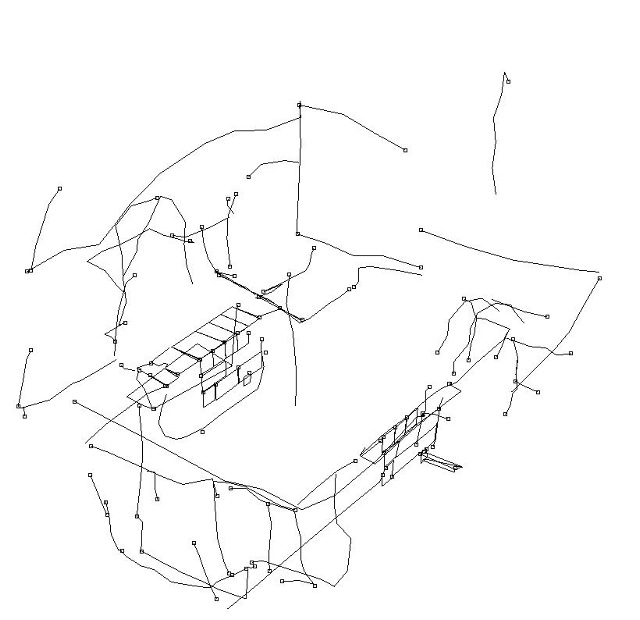Abb. 05-13: Der Datensatz für den Hohlraum. hoehle.igs (FB)

6. Sakristei der Alexanderkirche in Wildeshausen

Datenaufnahme 22.04.1995 von 12:16 bis 17:28 effektive Zeit: fünf Stunden

2D-Maßbandsystem für die Wände und 3D Tachymeter

Die Sakristei am südlichen Ende des Querhauses ist ein Rest des Klostergebäudes. An den Wänden befindet sich ein Freskenzyklus aus dem 15. Jahrhundert, der die Jugend und das Leiden Christi darstellt. 1954 fand man darunter eine weitere Schicht mit Gemälden aus der Zeit vor 1270, insbesondere eine schön gestaltete Falkenjagd.
https://de.wikipedia.org/wiki/Alexanderkirche_(Wildeshausen)#Sakristei

3D-Daten
sakristei.igs sakristei.dxf sakristei-alles-001.jpg

Abb. 06-01: Sakristei in Wildeshausen (FB)

Abb. 06-02: (FB)

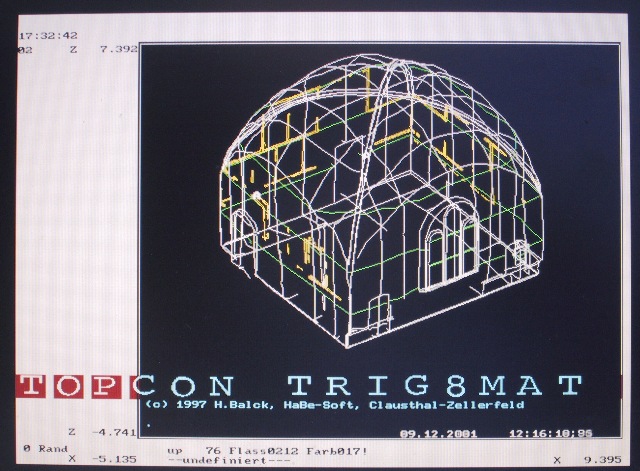Abb. 06-03:

Abb. 06-04: Daten von 2D- (Maßband) und 3D-Aufnahme (Tachymeter) (FB)

Abb. 06-05: Freskenzyklus (rot) 2D-Aufnahme mit Maßband (FB)

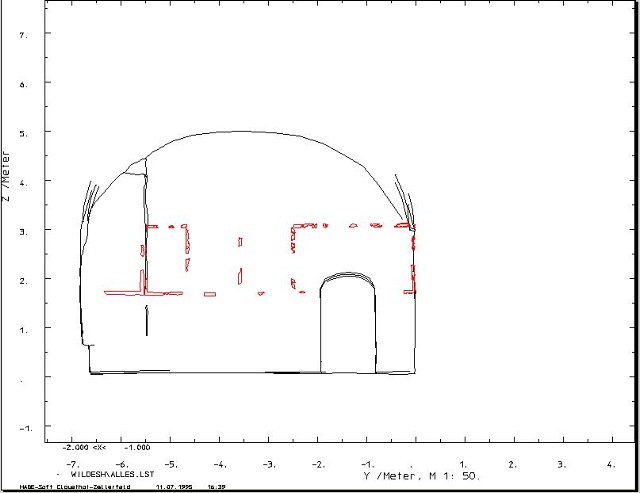Abb. 06-06: Freskenzyklus (rot) 2D-Aufnahme mit Maßband (FB)

Literatur: b-literatur.htm