Beobachtungen:
Obertöne, das Klangspektrum von Glocken und bei
Glockenspielen
Die folgenden Beispiele sind für Menschen mit musikalischer
Begabung gedacht. Es geht um das Hören.Was läßt sich aus Klängen heraushören? Was nehmen wir wahr?
Fast alle Musikinstrumente erzeugen Klänge, die sich aus mehreren Obertönen zusammensetzen. Frequenzanalyse
Wir nehmen die einzelnen Obertöne im Gemisch als solche nicht wahr, sondern ordnen den Klangcharakter dem Instrument zu, ohne zu wissen, daß die Summe der Obertöne für den speziellen Klang verantwortlich sind.
Die einzelnen Obertöne herauszuhören ist bei "harmonischen" Instrumenten auch sehr schwer, da die Töne ein ganzzahliges Vielfaches einer Grundfrequenz sind und daher mit ihnen ohne Schwebungen verschmelzen.
(Beispiel der schwingenden Saite in StehendeWellen )
Anders sieht es aus, wenn das Instrument aus mehreren voneinander unabhängig schwingenden Klangflächen besteht.
Eine Membrane (Pauke, Topfdeckel) oder eine Glocke besitzen eine Vielzahl von Einzelschwingungen, die nicht einfach das Vielfache einer einzigen Grundfrequenz sind. Diese Obertöne nennt man Partialtöne.
Gut hörbar wird dieses Phänomen besonders dann, wenn die verschiedenen Partialtöne gegeneinander "verstimmt" sind, und sich der Klang nach dem Anschlag zeitlich ändert, weil nicht alle Partialtöne die gleiche Lebensdauer haben.
Verstimmt oder zueinander passend? das ist ein wichtiges Kriterium für eine gute Glocke und auch für ein Geläut. glocken-tedeum
Den Klang der Glocken zu beschreiben ist ein komplizierter Vorgang, als Beispiel hier die Analyse der Glocken in der Neutstädter Marienkirche in Bielefeld:
http://www.biosensor-physik.de/glocken/glocken-marien-bielefeld.pdf
Eine Glocke, die unseren heutigen Vorstellungen entspricht, sollte etwa folgenden Tonaufbau haben:
(Oktave = 12 Halbtöne, 1200 Cent entspricht der doppelten Frequenz.
Die Aufteilung in Cent ist sehr viel feiner als das, was wir normalerweise bei sich bewegenden Glocken (Dopplereffekt) überhaupt wahrnehmen können. Daher gibt man häufig die Stimmung in 1/16 Halbton an. )
Beispiel für eine (theoretische) Glocke mit der Frequenz 4 * 440 Hz = 1720 Hz für den Partialton nominal
(Bezeichnungen nach Bill Hibbert, Great Bookham, Surrey www.hibberts.co.uk)
| tiefste Frequenz hum | Oktave prime |
Mollterz tierce | Quinte quint |
Oktave nominal | , , , , |
Oktave oct. nominal |
| 1 * f |
2 * f | 1,9 *f | 3 * f | 4 * f | |
8 *f |
| 440 Hz |
880 Hz |
1046 Hz |
1320 Hz |
1720 Hz |
3440 Hz |
|
| -24 Halbtöne | -12 Halbt. | -9 Halbtöne | -5 Halbtöne | 0 | |
+12 Halbt. |
| -2400 Cent |
-1200 Cent |
-900 Cent |
-500 Cent |
0 |
1200 Cent |
Die Glocke in dem folgenden Beispiel ist eine Stahlglocke in der St. Salvatoris-Kirche in Zellerfeld, Baujahr 1953.
Nach etwa 100 Jahren Erfahrung im Stahlguß hatte die Gießerei "Bochumer Verein" zu dieser Zeit eine musikalisch "saubere" Glocke produziert, die den obigen Vorstellungen entspricht.
| Frequenz / Hz |
Lautstärke / dB |
Abweichung / cent ideale Werte in ( ) 1 Halbton = 100 cent |
Name |
| 205.0 | 11.7 | -2400 (-2400) |
hum |
| 410.5 | 22.4 | -1198 (-1200) |
prime |
| 488.0 | 35.3 | -898 (-900) |
tierce |
| 614.5 | 5.9 | -499 (-500) |
quint |
| 820.0 | 16.4 | 0 | nominal |
| 1048.0 | 1.7 | 425
(400) |
|
| 1228.5 | 7.6 | 700
(700) |
superquint |
| 1431.5 | 1.8 | 965 |
|
| 1699.0 | 2.3 | 1261 (1200) |
oct. nominal |
Die Abweichungen zwischen den idealen und den gemessenen Werten sind vernachlässigbar.
Nur der sehr leise oberste Partialton ist ungefähr einen halben Halbton zu hoch ist.
Der dritte Ton in dieser Tabelle ist die Mollterz (charakteristisch für einen typischen Glockenklang in Mitteleuropa im Zeitraum der letzten Jahrhunderte). Er ist am Anfang mit 35 dB etwas lauter als alle anderen Partialtöne.
Im Verlauf von einigen Sekunden verschwinden (Abb. 02) die oberen Partialtöne und am Ende bleibt nach 20 Sekunden nur noch der tiefste Ton (englisch hum = summen) übrig.
Bei guten Bronzeglocken kann dieser Ton bis zu 60 Sekunden oder mehr nachklingen.
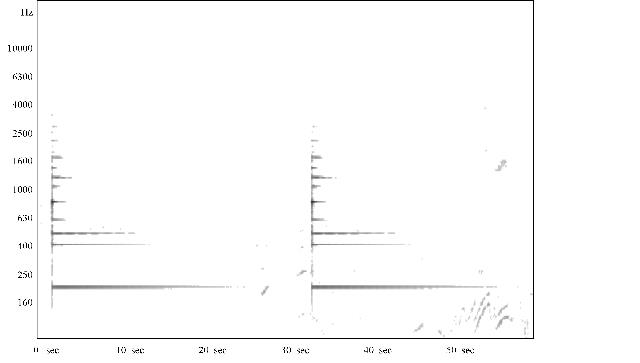 |
| Abb. 01: zwei Schläge
der
kleinen Stahlglocke in Zellerfeld, St. Salvatoris. Es gibt mehrere Obertöne, die tiefsten Töne schwingen am längsten. Mit gut geübtem Ohr kann man neben dem nominellen Anschlagton auch die anderen Töne hören, besonders den tiefen lange nachklingenden. Tondatei (Wave-Datei 210 kB), gesamte Datei Tondatei (Wave-Datei 1,3 MB) (Ganz rechts in der Analyse die Tonspur eines aufheulenden Motorrades.) (FB) |
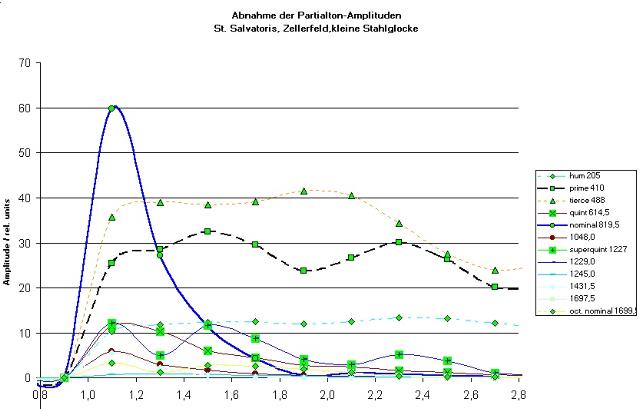 |
| Abb. 02: Zeitlicher
Verlauf der
Amplituden der Partialtöne dieser Stahlglocke. (FB) |
In St. Salvatoris gibt es eine Bronzeglocke vom Ende des 17. Jahrhunderts. Bei ihr erklingen weitere Obertöne.
Beim zweite Partialton
Tondatei (Wave-Datei, 780 kB)
Fragen zum Klangbeispiel der Stahlglocke:
Ist die Mollterz herauszuhören?
Kann man weitere Partialtöne wahrnehmen und mitsingen?
Wie lange hört man den untersten Ton?
Laut Frequenzanalyse gibt es Schwebungen bei der Mollterz (gestrichelte Linie), sind diese hörbar? Schwebung
Die folgenden Beispiele gehören zum Geläut der 1641 erbauten Holzkirche in Clausthal.
Es erfordert hohe Konzentration, wenn man die Glocken beurteilen will.
Die einzelnen Glocken:
Ist es ein sauberer Mollklang?
Sind die auf den Diagrammen sichtbaren Schwebungen bei einzelnen Partialtönen auch zu hören?
Das Geläut?
Wie würde es klingen, wenn die Glocken zusammen angeschlagen werden?
Ist das ein gut klingender Dreiklang c e g ?
Daten der Analyse
524 Hz (c = 523,3 Hz, Frequenzanalyse)
648,5 Hz (etwas tiefer als e =659,3 Hz)
1491,5 Hz (1491,5/2 = 745 Hz oder 729 Hz laut Tabelle??)
(etwas höher/tiefer als fis = 740 Hz, jedoch weit weg von g = 784 Hz)
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
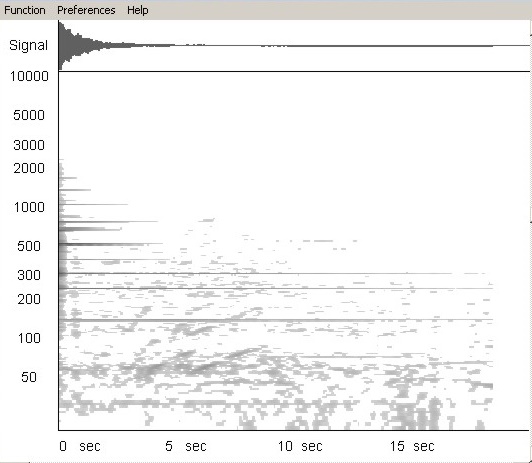
Abb. 03: Clausthaler
Marktkirche, große Glocke, Bronze 1792, Tondatei
(Wave-Datei: 430 kB) (FB)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
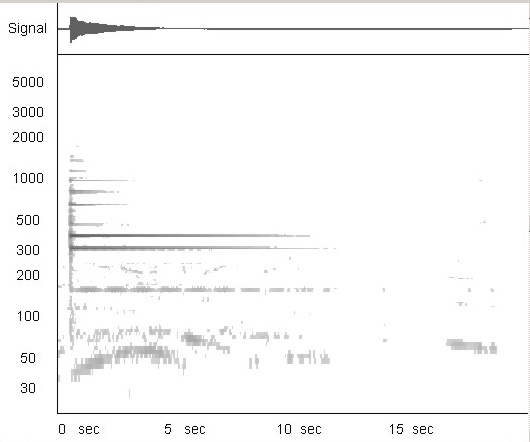
| Abb. 04: Clausthaler
Marktkirche, mittlere Glocke, Bronze,
1693, Tondatei
(Wave-Datei: 320 kB) (FB)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
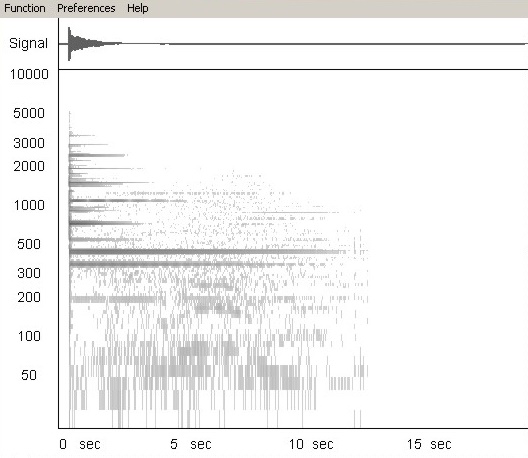
Abb. 05: Clausthaler
Marktkirche, kleine Glocke, Bronze
1921, Tondatei
(Wave-Datei: 430 kB) (FB)
Die Computer Analyse hat den Partialton nominal nicht richtig gefunden, er liegt eine Oktave tiefer als angegeben. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nachtrag Januar 2014
Die Auswertung der Daten stammt von 2003
2. Vergleich verschiedener Glocken
Die Zusammenstellung reicht von der Gloriosa in Erfurt bis zu kleinen Kuhglocken.
In den Darstellungen mit einer relativer Frequenzskala wird das typische (gewollte) Klangbild deutlich.
siehe oben: Oktave, hum (Unteroktave), Moll-Terz, (Quinte) Oktave usw.
Bei den vier Glockenspielen sieht man beispielsweise in Hahnenklee unterschiedliche "Handschriften" der Glockengießer.
Im oberen Bereich fallen drei Glocken aus dem üblichen Klangbild heraus
Die Daten stammen von eigenen Frequenzananlysen mit dem Programm von Bill Hibbert, Great Bookham, Surrey.
Tabelle, Daten mit Semicolon getrennt. (Excel-CSV-Format) alle-glocken-parameter-nur-daten.csv
Datenformat siehe Überschrift bzw. nachfolgendes Beispiel aus Erfurt
2.1 Schwingungsformen der Partialtöne
aus stehende-welle.htm
Stehende Wellen bei eindimensionalen Körpern haben ein einfaches Bildungsgesetz.
Bei zwei oder mehrdimensionalen Gebilden sind die Schwingungsmoden sehr viel komplexer.
 |
|
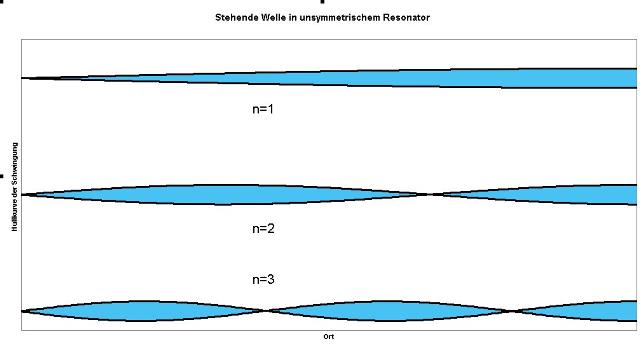
| Abb.
02-01: Eindimensionaler Körper (schwingende Saite,
lange dünne Orgelpfeife) Bildungsgesetz für stehende Wellen in einem unsymmetrischen Resonator, gedackte Orgelpfeife, die Wellenlängen der Obertöne sind ganzzahlige Teile der Resonatorlänge. Die zugehörigen Frequenzen sind ganzzahlige Vielfache der Grundfrequenz. (FB) |
|
 |
 |
| Abb. 02-01: ein
zweidimensionaler Körper (Aludraht) wird an der
Aufhängung periodisch hin und her geschwenkt. Der Draht ist auf seiner ganzen Länge homogen. Stehende Welle bei offenen Enden mit Knoten in der Mitte (die beiden Hälften entsprechen jeweils einem unsymmetrischen Resonator). vergleichbar mit einem Schnitt durch eine schwingende Glocke Ein elastischer Draht ist v-förmig nach unten gebogen, oben in der Mitte ist er an der Welle eines kleinen Elektromotors befestigt, der mit Wechselstrom einstellbarer Frequenz angetrieben wird. Schwingung erfolgt mit: 1 halbe Wellenlänge, Bauch-Knoten-Bauch: B-K-B Anregung erfolgt mit 7,5 Hz (FB) |
Abb. 02-03:
Stehende Welle
bei offenen Enden, 3 halbe Wellenlängen, B-K-B-K-B-K-B Anregung erfolgt mit 29,4 Hz (FB) |
 |
 |
| Abb. 002-04: stehende
Welle bei
offenen Enden, 5 halbe Wellenlängen B-K-B-K-B-K-B-K-B-K-B Anregung mit 91 Hz (FB) |
Abb. 02-05: stehende
Welle bei
offenen Enden, 7 halbe Wellenlängen B-K-B-K-B-K-B-K-B-K-B-K-B-K-B Anregung mit 162 Hz (FB) |
Die Form der Rippe einer Glocke entscheidet über die Frequenzen der unterschiedlichen Schwingungsmoden (Partialtöne)
Sie ist ein gut gehütetes Geheimnis der Glockengießer.
Von ihr hängt ab, aus welchen Tönen bzw. Frequenzen sich der Klang zusammensetzt.
Extrem wichtig ist, daß die Glocke in jeder Höhe eine einheitliche Wandstärke besitzt, d.h. beim Bau der Gußform muß die Schablone der Rippe korrekt übernommen werden. Auch darf beim Gießen sich die Form an keiner Stelle erweitern.
"Unrunde" Glocken erkennt man an akustischen Schwebungen.
Auch starke Abnutzung am Schlagring durch Klöppel oder Hammer führt zu ungleicher Materialverteilung und damit zu Schwebungen. Dies ist häufig bei Uhrglocken zu hören.
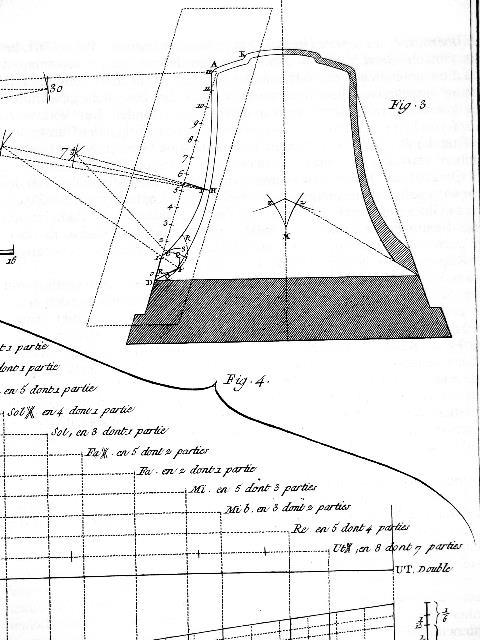 |
| Abb. 02-06: Form einer Glocke, Fontes
de Cloches (Diderot Encyclopédie, 1751-1772, aus Michaelstein Band Nr. 56, S. 91) |
 |
| Abb. 01-07: Nach den Maßen der Skizze
von Diderot. Im unteren Bereich ist die Wandstärke groß für den Anschlag des Klöppels. Oben ist sie klein, damit der Körper gute elastische Eigenschaften bekommt. (FB) |
 |
| Abb. 02-08: Hier ist die
Materialstärke noch dünner. Gesprungene
Glocke, Glockenmuseum Apolda (FB) |
 |
| Abb. 02-09: Nach den Maßen der Skizze von Diderot (FB) |
 |
Abb. 02-10: Glocke aus dem Erfurter
Dom. Am Schlagring (beim Kreis in der Zeichnung) ist
die Wand 184 mm stark."Rippe der Erfurter großen Glocke Maria glor.Zeichnung aus dem Glockenmuseum Laucha (FB) |
 |
| Abb. 02-11: Am unteren Rand der Glocke, dem Schlagring, hat der Klöppel schon einiges Material abgetragen (links innen). Aber auch in der Mitte hinten sind Abnutzungen zu sehen, d. h. die Glocke wurde im Laufe ihres Lebens schon einmal um 90 Grad gedreht. Stiftskirche Herrenberg (FB) |
 |
| Abb. 02-12: Bei einer Stundenglocke
schlägt häufig ein Hammer von außen und nicht der
Klöppel. Starke Abnutzung außen am Schlagring , Glockenmuseum in Laucha (FB) |
 |
| Abb. 02-13: Schon nach wenigen Jahren
sind die Anschlagstellen deutlich zu sehen.
Neustädter Marienkirche, Bielefeld (FB) |
  |
| Abb. 02-14: Verformung der Glocke am
Schlagring nach dem Anschlag des Klöppels.
Darstellung stark überhöht. Es gibt auch noch
weitere Schwingungsmoden mit einer größeren Anzahl
von Schwingungsknoten und Bäuchen. (FB) |
2.2 Beispiel für Erfurter Dom, Gloriosa
 |
| Abb. 02-15: Gloriosa in Erfurt nach
der letzten Reparatur. 12 Tonnen Bronze, gegossen
1497 Foto: Original date/time: 2010:04:11 14:44:20 (FB) |
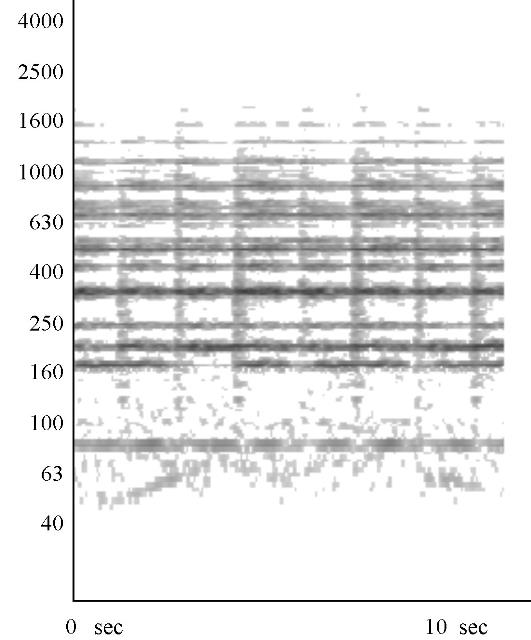 |
| Abb. 02-16: Das Klangspektrum der
Gloriosa nach einer Tonaufnahme in einer
Fernsehsendung vom Dezember 2004. (FB) "Am 8. Dezember 2004 wurde sie das erste Mal nach der Reparatur wieder geläutet" de.wikipedia.org/wiki/Gloriosa_%28Erfurter_Dom%29 siehe auch www.bistum-erfurt.de/front_content.php?idcat=1857 |
| Offset für Nummer in der Liste |
Dateiname, Nominalfrequenz | Summe der Amplituden | offset |
|||
| 3 | gl-dom-erfurt-02.wav, 334,50 | 84.0 | 0 | |||
| Frequenz / Hz | Amplitude | relative Amplitude, Summe = 100% | Abweichung in Cents | Abweichung in Cents + Offset | ||
| 31 | 81.0 | 5.1 | 6.1 | -2455 | hum | -2455 |
| 31 | 168.0 | 24.2 | 28.8 | -1192 | prime | -1192 |
| 31 | 200.5 | 15.2 | 18.2 | -886 | tierce | -886 |
| 31 | 243.0 | 3.8 | 4.5 | -553 | quint | -553 |
| 31 | 334.5 | 19.6 | 23.3 | 0 | nominal | 0 |
| 31 | 425.0 | 3.3 | 4.0 | 415 | 415 | |
| 31 | 486.0 | 7.4 | 8.8 | 647 | superquint | 647 |
| 31 | 669.5 | 3.9 | 4.6 | 1201 | oct, nominal | 1201 |
| 31 | 881.0 | 1.5 | 1.8 | 1677 | 1677 |
Die Glocke hat ein reichhaltiges Spektrum an Teiltönen und entspricht sehr gut unseren Klangvorstellungen.
Die "Oktaven" liegen mit -2455, -1192 und 1201 Cent sehr nahe an den idealen Werten von 2400 und 1200 Cent (24 bzw. 12 Halbtöne).
Damit ist sie mit ihren fast 12 Tonnen eine exzellentes Beispiel der Glockengießerkunst für die Zeit.
"Wie ihre Inschrift verrät, goss der Glockengießer Gerhard Wou von Kampen die Gloriosa im Juli 1497. Seine Technik und sein Können sind bis heute unerreicht." www.bistum-erfurt.de/front_content.php?idcat=1857
2. 3 Die Zusammenstellung aller Glocken
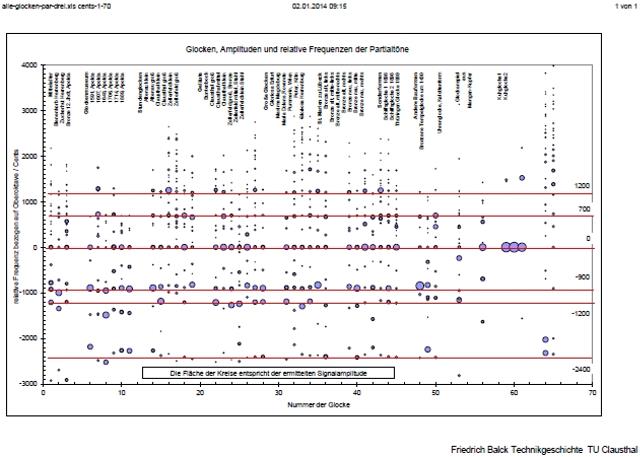 |
| Abb. 02-17:Partialtöne verschiedener
Glocken, relative Frequenzskala in Cents (1/100
Halbton) Die Fläche der Kreise entspricht der ermittelten Signalamplitude (Lautstärke). Zur Orientierung sind die roten Linien eingezeichnet von oben: +1200 Cent 12 Halbtöne nach oben ( octav nominal Oktave darüber) +700 Cent 7 Halbtöne nach oben ( super quint Quinte darüber) 0 Bezugston ( nominal ) -900 Cent 9 Halbtöne nach unten ( tierce MollTerz über der Oktave darunter) -1200 Cent 12 Halbtöne nach unten ( prime Oktave darunter) -2400 Cent 24 Halbtöne nach unten ( hum zwei Oktaven darunter) Die Frequenzen einer jeden Glocke sind in dieser Darstellung so normiert, daß der Partialton nominal bei 0 liegt. In dieser logarithmischen Darstellung kann man daher gut sehen, ob die Abstände der übrigen Partialtöne dazu gleiche Abstände haben. Die Positionen der roten Linien entsprichen einer guten europäischen Glockentradition. (Bei Glocken müssen die Partialtöne sich nicht wie die Obertöne einer Saite verhalten und in den Frequenzverhältnissen 1, 2, 3, 4, 5, 6 usw auftreten. ) Bei den Glocken von Nr. 4 bis 9 wird die im Klangbild uns vertraute Mollterz nicht erreicht. Auch die Glocken ganz rechts haben völlig andere Partialtöne. Kompletter Datensatz alle-glocken-par-drei-cents-1-70.pdf Die Glocken der Reihe nach von links nach rechts: Glockenmuseum Herrenberg und Apolda 1 Bienenkorb Herrenberg 2 Zuckerhut Herrenberg 3 Bronze 12.Jhdt, Apolda 4 1591, Apolda 5 1607, Apolda 6 1648, Apolda 7 1706, Apolda 8 1714, Apolda 9 1889, Apolda Stundenglocken 10 Altenau klein 11 Altenau groß 12 Clausthal klein 13 Clausthal groß 14 Zellerfeld klein 15 Zellerfeld groß Geläute 16 Buntenbock 17 Clausthal groß 18 Clausthal mittel 19 Clausthal klein 20 Zellerfeld groß, Bronze 21 Zellerfeld mittel, Stahl 22 Zellerfeld klein Stahl Große Glocken 23 Gloriosa Erfurt 24 Maxima Magdeburg 25 Maria Dolens,Rovereto 26 Pummerin, Wien 27 Peter, Köln 28 Gloriosa Herrenburg 29 St. Marien zu Lübeck 30 Bronze alt, links 31 Bronze alt, mitte-links 32 Bronze alt, mitte-rechts 33 Bronze alt, rechts 34 Bronze neu, links 35 Bronze neu, mitte 36 Bronze neu, rechts Sonderformen 37 Schiffsglocke 1 1898 38 Schiffsglocke 2 1898 39 Thüringen Glocke 1989 Andere Bauformen 40 Bronzene Tempelglocke um 1430 41 Uhrenglocke, Kalottenform 42 Glockenspiel aus Mangan-Kupfer 43 Kuhglocke1 44 Kuhglocke2 (FB) |
 |
|
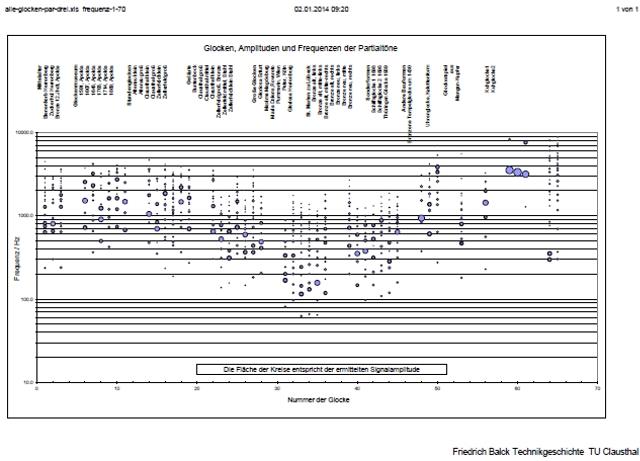
Abb. 02-18:
Partialtöne verschiedener Glocken, absolute Frequenzskala, logarithmisch alle-glocken-par-drei-frequenz-1-70.pdf (FB) |
 |
| Abb. 02-19: Partialtöne der Glocken
von vier Glockenspielen, relative Frequenzskala in
Cent St. Marien zu Lübeck (36 Bronzeglocken), TU-Clausthal am Feldgraben (25 Stahlglocken), Zellerfeld am Markplatz (16 Bronzeglocken), Hahneklee (32 Bronzeglocken) alle-glocken-par-drei-cents-70-192.pdf (FB) |
 |
| Abb. 02-20: Partialtöne der Glocken
von vier Glockenspielen, absolute Frequenzskala,
logarithmisch St. Marien zu Lübeck (36 Bronzeglocken), TU-Clausthal am Feldgraben (25 Stahlglocken), Zellerfeld am Markplatz (16 Bronzeglocken), Hahnenklee (32 Bronzeglocken) alle-glocken-par-drei-frequenz-70-192.pdf (FB) |
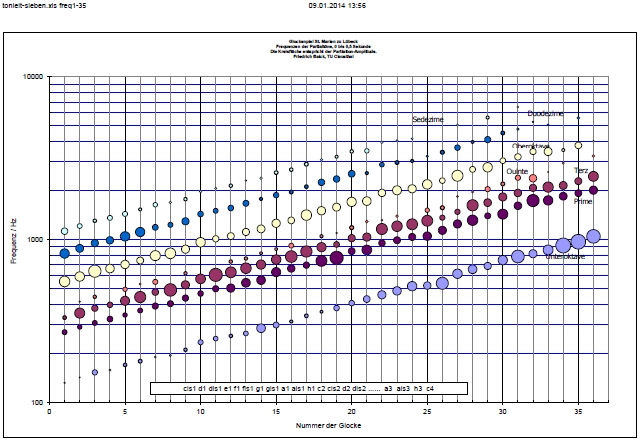 |
| Abb. 02-21: Ausschnitt:
Partialtöne der 36 Glocken von St. Marien zu Lübeck,
Frequenzen Die Fläche der Kreise entspricht der ermittelten Signalamplitude (Lautstärke). Bei vielen ist die Mollterz (dritte von unten) sehr viel kräftiger als die Prime (zweite von unten). Oberhalb von der Glocke 11 scheint ein anderes Partialtonspektrum vorzuliegen. (andere Bauform?) (FB) |
 |
| Abb. 02-22: Glockenspiel, St. Marien
zu Lübeck. Die Glocken stammen teilweise aus der
Katharinenkirche in Danzig. Man findet zwei
unterschiedliche Ausführungen (andere Giesserei?) Die Glocken können manuell (Klöppel mit Seilzug) oder von einem mechanischem Schaltwerk (zwei Hämmer pro Glocke) gespielt werden. Foto: Original date/time: 2003:08:05 11:09:37 (FB) |
 |
www.biosensor-physik.de | (c)
22.11.2007 F.Balck - 28.11.2024 |
© BioSensor-Physik 2014 · Impressum
