Friedrich Balck > Biosensor > Physik > Frequenz-Analyse

Beobachtungen:

Frequenzanalyse, Obertöne

verwendetes Programm:
Spectrogram, Richard Horne, Visualization Software LLC, www.visualizationsoftware.com
kostenlos ältere Freeware-Version unter: http://fledermaus.wtal.de/spectro1.htm

Fourier-Analyse: Zerlegung einer periodischen Schwingung in eine Summe aus einzelnen Sinus-Schwingungen variabler Amplitude und Phase. Die Frequenzen der Komponenten sind ein ganzzahliges Vielfaches einer Grundfrequenz.

Anschaulich: Stehende Wellen auf einer schwingenden Saite sind nur dann möglich, wenn die Wellenlänge ein ganzzahliger Teil der Seitenlänge ist. Also kann der Ton einer Saite sich nur aus solchen Schwingungen zusammensetzen. Auch für andere Musikinstrumente beispielsweise Posaune gilt dieses entsprechend.


Abb. 01: Modell für die Darstellung der Frequenzanalyse, bei der Klaviertastatur gibt es eine logarithmisch angeordnete Folge der Frequenzen. Bei jeder Oktave (Abstand 12 Halbtöne = Wiederholung des Tastenmuster) verdoppelt sich die Frequenz. (FB)	Abb. 02: Frequenzanalyse: Mehrstimmiger Satz aus reinen Sinusschwingungen. Der Mond ist aufgegangen. In dieser Form ist die Analyse nahezu als Notenvorlage zu verwenden. Die Frequenz ist logarithmisch nach oben aufgetragen, nach rechts die Zeit. In der oberen Spur erscheint die Lautstärke. (FB)

Abb. 03: Frequenzanalyse eines einfachen Kinderliedes, das verwendete Instrument produziert eine reine Sinusschwingung. (FB)	Abb. 04: Elektronisch generierte Töne mit gleitend veränderter Frequenz (Sweep). Ist die Änderung sehr schnell (Chirp) verschmilzt der Ton zu einem breiten Klang (rechts). Sweep (FB)

Abb. 05: Mit einem einfachen Brett mit Nägeln lassen sich nahezu Sinus-Schwingungen erzeugen (FB)

Abb. 06: Mikrofonsignal gegen die Zeit beim Anzupfen eines Nagels. Es sieht aus wie eine leicht modulierte Sinus-Schwingung. (FB)	Abb. 07: Tonleiter mit Nägeln gespielt, Frequenzanalyse (lineare Skala). Neben leichtem Rauschen beim Anzupfen ist nur jeweils eine Frequenz besonders ausgeprägt. (FB)

Abb. 08: Mikrofonspannung, Saite gezupft, nach dem Zupfen. Der Kurvenverlauf ist nahezu sinusförmig. (FB)

Abb. 09: Mikrofonspannung,
Saite ohne Resonanzkörper, Saite mit Bogen gestrichen.
Der Kurvenverlauf ist sägezahnförmig. Beim Anstieg wird die Saite vom Bogen mitgenommen, beim Abfall schwingt sie frei zurück. Es wechseln zwei Prozesse nacheinander: zurückgleiten-festhaften = slip-stick. In der Anstiegsflanke ist mindestens eine weitere Sinusschwingung sichtbar.

Zum Vergleich die Schwingung einer gestrichenen Cello-Saite mit Resonanzkörper. oberton-saite (FB)

Abb. 10: Zuordnung der Klaviertastatur zu Frequenzen. Pro Oktave nach oben oder unten verdoppeln bzw. halbieren sich die Frequenzen. Bei der (gebräuchlichen) wohltemperierten Stimmung ist der Frequenz-Abstand eines Halbtonschritts definitionsgemäß
die 12. Wurzel aus 2 = 1,059.
Um auch kleinste Verstimmungen genau angeben zu können, teilt man einen Halbtonschritt auf in 100 % und nennt diese Teilung dann Cent. 1200 Cent entspricht dann 12 Halbtönen also einer Oktave. (FB)

Abb. 11: Zug-Posaune mit Mundstück (FB)

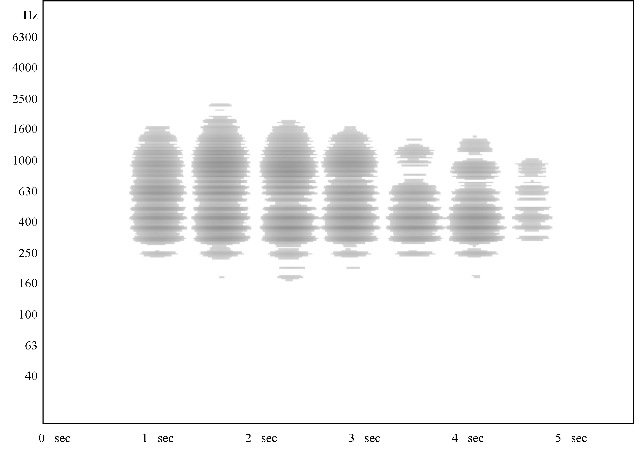Abb. 12: Frequenzanalyse: Auf das Mundstück der Posaune sieben mal mit der flachen Handfläche geklopft. Die tieferen Obertöne (ca. 120, 180, 240 Hz) und der Grundton (ca. 60 Hz) sind bei dieser Anregung nur schwach und daher kaum zu erkennen. Im oberen Frequenzbereich oberhalb von etwa 1000 Hz ist deutlich eine fast kontinuierliche Abfolge von Tönen zu erkennen. (FB)

Abb. 13: Frequenzanalyse: Klatschen auf das Posaunenmundstück. Die aus dem oberen Bild ermittelten Frequenzen zeigen eine lineare Folge von Obertönen mit (rechnerisch) mittlerem Abstand von 60,5 Hertz. Die beiden noch fehlenden unteren Töne (Grundton ca 60 Hz und der erste Oberton mit ca. 120 Hz) waren sehr schwach. (FB)

Abb. 14: Alle Obertöne eines C-Instrumentes: Nicht alle Obertöne (7, 9, 11, 13) klingen so "sauber", daß man sie exakt auf die Notenlinien schreiben kann. Tondatei (Wave-Datei 360 kB) (FB)

Abb. 15: Tonleiter über zwei Oktaven auf einer Klarinette gespielt. Jeder Ton besteht aus einer Folge von vielen Obertönen, die insgesamt den typischen Klang eines Instrumentes ausmachen. Im unteren Bereich ist bei einer Klarinette konstruktionsbedingt der erste Oberton (doppelte Frequenz des Grundtons) und die anderen ungeraden Obertöne nur sehr schwach zu hören. Nach oben sind die Frequenzen begrenzt durch die Aufnahmeeigenschaften des Speichermediums. (FB)

Abb. 16: Einzelne Töne auf der Klarinette gespielt (Dur-Dreiklänge). In der oberen Spur ist die Signal-Lautstärke aufgetragen. Die Analyse reicht beim ersten Ton bis über den 20. Oberton hinaus (21-fache der Grundfrequenz). Begrenzung der Frequenz nach oben durch Speichermedium. (FB)

Abb. 17: Andere Darstellung: Lautstärke gegen die Frequenz, (senkrechter Schnitt durch die vorherige Abbildung bei der Zeit 6,1 Sekunden). Deutlich sichtbar ist die Abschwächung jedes zweiten Obertones. (FB)

Nachtrag 26.11.2019

Zur Theorie der Instrumente:
zylindrisches Rohr - ungerade Harmonische, die geraden sind schwach ( s. Abb. 15)
    Klarinette
konisches Rohr     - alle Harmonische kommen vor.
    Saxophon, Oboe, Blechblasinstrument

Klarinette und Saxophon haben den gleichen Aufbau beim Mundstück, sie unterscheiden sich in der Form des Klangkörpers.
Bei der Klarinette sind im unteren Register nur die ungeraden Harmonischen vorhanden, beim Saxophon gibt es alle.

http://newt.phys.unsw.edu.au/jw/woodwind.html

Abb. 02-01: Mundstück einer Klarinette mit einem Rohrblatt (FB)

Abb. 02-02: Frequenzanalyse, Mundstück einer Klarinette (rechts), durch Verändern des Anpreßdrucks kann man die Tonhöhe verändern.
Es gibt eine lineare Abfolge von Harmonischen mit nahezu gleichen Intensitäten.
ca. 800 Hz, 1600 Hz, 2400 Hz, 3200 Hz. (FB)

Abb. 02-03: Mundstück einer Klarinette und Kopfstück einer Sopran-Blockflöte (FB)

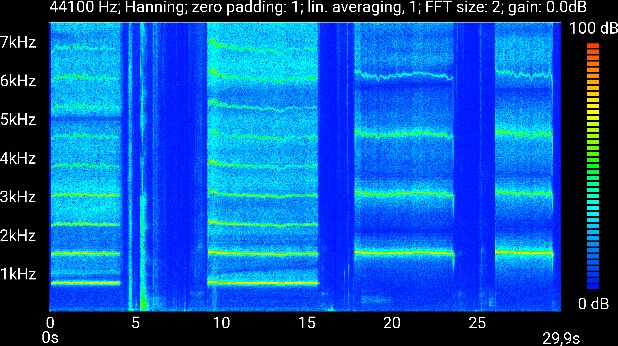Abb. 02-04: links: Mundstück der Klarinette, rechts: Kopf der Blockflöte
beide Analysen zeigen lineare Abfolge von Harmonischen mit nahezu gleicher Intenstität. (FB)

Abb. 02-05: Mündstücke für Trompete (unten) und Tenorhorn (oben) (FB)

Abb. 02-06: Mundstücke ohne Instrument:
links: Blockflöte, in der Mitte: Trompete, rechts: Tenorhorn (FB)

Abb. 02-07: Klarinette mit kurzem und längerem zylindrischen Kupferrohr (15 mm Durchmesser außen) (FB)

Abb. 02-08: in der Mitte: kurzes Kupferrohr, rechts: langes Kupferrohr.
Beim langen Rohr zeigt sich eine unterschiedliche Intensität der geraden und ungeraden Harmonischen.
Die geraden sind schwächer, die ungeraden kräftiger. (FB)

Abb. 02-09: Mundstück vom Tenorhorn mit Kupferrohr. (FB)

Abb. 02-10: links, Mitte: Klarinette, rechts: Mundstück Tenorhorn, kein Unterschied bei der Intensität von geraden/ungeraden Harmonischen (FB)

Abb. 02-11: Mundstück Tenorhorn mit Plastikschlauch

Abb. 02-12: links Klarinette, Mitte: Tenorhorn Kupferrohr, rechts: Mundstück Tenorhorn mit Plastikschlauch, gleiche Intensität der Harmonischen (FB)

Abb. 02-13: Klarinette mit konischem Schallkörper (Schalltrichter einer Trompete) (FB)

Abb. 02-14: Mitte: Klarinette mit konischem Schallkörper ( wie beim Saxophon). Die gerade und ungerade Harmonische unterscheiden sich kaum in der Intensität. (FB)