Friedrich Balck > Biosensor > Physik > Stehende Wellen

Beobachtungen:

Stehende Wellen, erhöhte und erniedrigte Intensität an verschiedenen Orten

Bei der Ausbreitung von Wellen wird Energie übertragen. Bei Wasserwellen ist die Wellenhöhe ein sichtbares Maß für deren Energie. Wenn die Wellen sich ausbreiten, nehmen sie ihre Energie mit.

Kommt es allerdings zu Reflexionen an beispielsweise Hindernissen, dann können sich Wellen mit entgegengesetzter Richtung überlagern. Haben in diesem Fall die Wellen gleiche Frequenz, dann kann die hintransportierte Energie genauso groß sein wie die zurückkommende. Dies bedeutet, daß kein Energietransport stattfindet und die Schwingung somit lokal an festen Orten zu finden ist. Es gibt ortsfest Bäuche mit starker Schwingung und daneben Knoten, bei denen keine Schwingung auftritt.

Ein klassisches Beispiel hierfür ist eine schwingende Saite.


Abb. 01: Laufende Wellen werden am Ende des Gefäßes reflektiert. Aus der Überlagerung von hin- und rücklaufenden Wellen können sich Stehende Wellen bilden. (FB)	Abb. 02: Wasserwelle, den Abstand zwischen zwei Bergen oder Tälern nennt man Wellenlänge. (FB)

Abb. 03a: Stehende Wellen auf einem Gummiseil, zwei halbe Wellenlängen passen auf das Seil. (FB)	Abb. 03b: Stehende Wellen auf Gummiseil, fünf halbe Wellenlängen , die Frequenz ist 5/2 = 2,5 mal höher als im linken Bild. (FB)

Abb. 03c: kleiner Gleichstrom-Motor, Wechselspannung aus dem Frequenzgenerator (FB)

Abb. 04a: Stehende Welle auf dem Zugseil eines Skiliftes beim Sonnenuntergang. (FB)	Abb. 04b: bei Tage (FB)

Abb. 05: Bildungsgesetz für stehende Wellen in einem symmetrischen Resonator, schwingende Saite (FB)

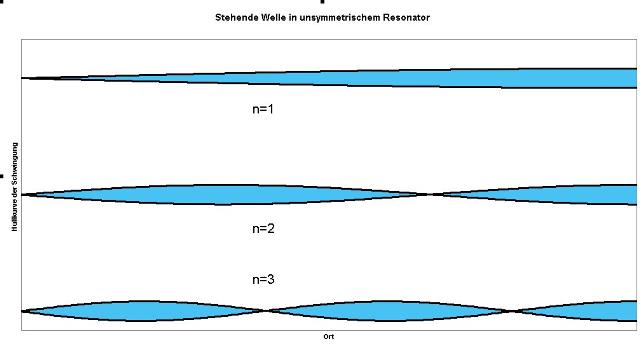
Abb. 05a: Bildungsgesetz für stehende Wellen in einem unsymmetrischen Resonator, gedackte Orgelpfeife (FB)

Abb. 05b: Stehende Welle bei offenen Enden mit Knoten in der Mitte (die beiden Hälften entsprechen jeweils einem unsymmetrischen Resonator). vergleichbar mit einem Schnitt durch eine schwingende Glocke Ein elastischer Draht ist v-förmig nach unten gebogen, oben in der Mitte ist er an der Welle eines kleinen Elektromotors befestigt, der mit Wechselstrom einstellbarer Frequenz angetrieben wird. Schwingung erfolgt mit: 1 halbe Wellenlänge, Bauch-Knoten-Bauch: B-K-B Anregung erfolgt mit 7,5 Hz (FB)	Abb. 05c: Stehende Welle bei offenen Enden, 3 halbe Wellenlängen, B-K-B-K-B-K-B Anregung erfolgt mit 29,4 Hz (FB)

Abb. 05d: stehende Welle bei offenen Enden, 5 halbe Wellenlängen B-K-B-K-B-K-B-K-B-K-B Anregung mit 91 Hz (FB)	Abb. 05e: stehende Welle bei offenen Enden, 7 halbe Wellenlängen B-K-B-K-B-K-B-K-B-K-B-K-B-K-B Anregung mit 162 Hz (FB)

Abb. 05f: Kundtsches Klangrohr mit Korkmehl zum Sichtbarmachen stehender Wellen. Rechts am Rohrende befindet sich ein Lautsprecher, der die Luft im Rohr zum Schwingen anregt. Die Wellenlänge der Schwingung ist etwa doppelt so lang wie der Bildausschnitt. (FB)

Abb. 05g: Neben der Grundschwingung mit Wellenlänge von vielen Zentimetern gibt es auch Schwingungen mit sehr kurzer Wellenlängen, hierbei türmen sich die Staubteilchen in sehr engen Bereichen hoch auf. (FB)
Eisenstab siehe auch wellen.htm#eisenstab

Abb. 06a: Stehende Wellen in einem Festkörper. Ein Eisenstab (Stahl) wird bei geeigneter Frequenz (Resoananz bei 1984 Hz) durch den Wechselstrom in einer Spule zum Schwingen angeregt. resonanz Mit dem Mikrofon am Ende läßt sich die Schwingung messen. Verschiebt man die Spule über den Stab, so ändert sich das Mikrofonsignal. 28.11.2003 (FB)

Abb. 06aa: Der Stab liegt auf Watte (rechts). Die Anregespule umschließt ihn. Sie wird mit einem Seilzug bei konstanter Geschwindigkeit entlang gezogen. Ein Holzrahmen dient zur Führung. 08.12.2003 (FB)

Abb. 06ab: Das andere Ende vom Stab mit Watte und Mikrofon rechts daneben, 08.12.2003 (FB)

Abb. 06b: Frequenzanalyse des Mikrofonsignals als Funktion der Position der Spule. Offensichtlich bilden sich stehende Wellen aus im Stab. frequenzanalyse Es sind hier bis zur zehnten Oberwelle Schwingungen festzustellen. Ganz oben ist die Lautstärke des Gesamtsignals zu erkennen, die in der Stabmitte sehr viel geringer ist. Bei den einzelnen Oberschwingungen erkennt man deutlich die Knoten und Bäuche, beispielsweise sind bei der obersten (zehnten) Oberwelle neun Knoten zu sehen. (FB)

Abb. 06c: Die Signalamplitude für verschiedene Oberschwingungen als Funktion der Position des Magneten, deutlich sichtbar Knoten und Bäuche, logarithmische Auftragung der Amplidute. Die zugehörigen Frequenzen sind rechts in der Legende (obere Hälfte) 1984 bis 13891 Hz zu erkennen. eisenstab-motor-02.wav (FB)

ABb. 06d: die Frequenzen gehören zu einer Reihe von Harmonischen mit Abstand 1949 Hz Bei einer Stablänge von 1,5 m wäre das eine Schallgeschwindigkeit von 5847 m/s eisenstab-motor-02.wav (FB)
Xylophon mit akustischen Rohren

Abb. 07a: Konzert-Xylophon, unter den hölzernen Klangstäben hat man Resonanzröhren angebracht. Das sind nach unten geschlossene quaderförmige oder zylindrische Hohlkörper, die den Klang beeinflussen und die Abstrahlung verstärken. In den Röhren bilden sich stehende Wellen aus, die bei richtiger Abstimmung ihrer Länge Energie aus der Schwingung der Holzstäbe erhalten. gekoppelt Die tiefen Töne des Instrument verhalten sich bezüglich ihrer Oberschwingungen wie die einer klingenden Saite oder einer Orgelpfeife. Bei der Tonerzeugung gibt es allerdings einen Unterschied zur Saite, denn beim Holz sind die Enden lose, d.h. nicht eingespannt. Erst kurze Zeit nach dem Anschlag erreichen die tiefen Töne beim Grundton ihre maximale Lautstärke. Das Klangholz koppelt seine Energie in die Resonanzröhren ein. Hierbei vergeht hörbar eine Zeit von etwa einer viertel Sekunde, bis die maximale Lautstärke erreicht ist. xylophon (FB)
siehe auch Membranen blechblasinstrument-06.htm#kapitel-06-01

Abb. 08a: Stehende Wellen zwischen Schiffswand (oben) und Kaimauer (unten). Sie werden von den Schwingungen des Schiffmotors angeregt. (FB)	Abb. 08b: Stehende Wellen, Ausschnitt (FB)

Abb. 09a: Stehende Wellen auf der Wasseroberfläche einer Klangschale, hier am Rande der Schale. Man reibt mit leicht angefeuchteten Fingern auf dem Rand der Schale und regt sie damit zum Schwingen an. Das Wasser in der Schale zeigt dann die verschiedenen Schwingungsformen an. (FB)	Abb. 09b: Stehende Wellen auf der Wasseroberfläche einer Klangschale, hier in der Mitte der Schale. (FB)

Abb. 09c: stehende Wellen auf einer Wasseroberfläche, angeregt vom Wind (FB)

Abb. 09c: Sand auf einer Messingplatte, sie wurde mit einem Lautsprecher zum Schwingen angeregt. Der Sand zeigt die Stellen, an denen sie bei der Schwingung in Ruhe war, so genannte Knotenlinien. (FB)

Abb. 09d: Chladni- Klangfiguren auf einer Messingplatte, mit Sand bestreut, von unten mit einem Lautsprecher zum Schwingen angeregt. (FB)	Abb. 09e: Der Sand verteilt sich auf andere Weise, wenn man die Frequenz verändert. (FB)

Abb. 10: Eine Gummimembrane mit aufgezeichnetem Strichgitter ist über ein Lautsprechergehäuse gespannt. Der Lautsprecher wird mit unterschiedlichen Frequenzen angeregt. (FB)	Abb. 11: Stehende Wellen, Schwingungen der Gummimembrane werden sichtbar durch das Strichgitter. Chladni-Klangfiguren. (FB)

Abb. 12: Stehende Wellen, die Membrane schwingt an einigen Stellen, an anderen ist sie ruhig. (FB)	Abb. 13: Stehende Wellen, das Schwingungsmuster hängt von der Frequenz ab. (FB)

Abb. 13a: Eine Membrane ist auf eine Lautsprecherbox gespannt und wird von vorne mit einem Scheinwerfer beleuchtet. Schwingt der Lautsprecher, so bewegen sich bei geeigneten Frequenzen Teile der Mebrane in Resonanz mit. resonanz (FB)	Abb. 13b: Das Scheinwerferlicht wird nur an einigen Stellen in das Kameraobjektiv reflektiert. Stehende Wellen sind erkennbar. Es sind Klangfiguren, benannt nach Chladni. (FB)

Abb. 13c: Stehende Wellen auf der Membrane: von außen nach innen gibt es eine Knotenlinie, um die Symmetrieachse herum vier Bereiche. (FB)	Abb. 13d: bei höherer Frequenz treten zusätzliche Bäuche und Knotenlinien auf. (FB)

Abb. 13d1: Konzertpauke, über einen Metallkessel ist ein Fell gezogen und mit verstellbaren Klammern gespannt. (FB)	Abb. 13d2: Dunkler Sand lagert sich an einigen Stellen an, wenn man die Membrane mit Hilfe eines Lautsprechers zum Schwingen anregt. Es entstehen Chladni-Klangfiguren. (FB)

Abb. 13d3: Je nach Frequenz der Anregung ergeben sich unterschiedliche Muster auf mit Sand bestreuten Membrane. (FB)	Abb. 13d4: Ausschnitt, Sandhaufen,noch nicht verteilt. (FB)
	http://de.wikipedia.org/wiki/Richtcharakteristik http://de.wikipedia.org/wiki/Antennendiagramm
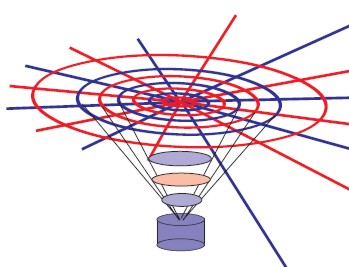
Abb. 13e: In einer Beobachtungsebene oberhalb der Membrane beobachtet man eine nichthomogene Verteilung der Schallintensität. Sie besteht näherungsweise aus Kegelschnitten (Kreisen) und radialen Strahlen. An den Schnittpunkten beide Systeme gibt es Überlagerung mit Verstärkung und Auslöschung.(FB)	Abb. 13f: Abstrahlverhalten einer Parabol-Antenne.

Abb. 13e: Die Kunst des Glockenbaus. Wie muß die Form gestaltet sein, damit die vielen möglichen Schwingungsformen musikalisch zueinander passen. (Form einer Glocke, Fontes de Cloches (Diderot Encyclopédie, 1751-1772)	Abb. 13f: Klangspektrum einer Glocke. kleine Uhrglocke der Clausthaler Marktkirche Es gibt viele Frequenzen, die gleichzeitig erklingen. frequenzanalyse (FB)

Abb. 14: Antennenmast für Fernsehen bei unterschiedlichen Wellenlängen. Man versucht den Abstand der Stäbe einer Antenne der Wellenlänge anzupassen, um optimalere Empfangsbedingungen zu haben. Bei exakten Abständen können sich stehende Wellen auf der Antenne bilden. Für die höheren Frequenzen der Fernsehsateliten (Mikrowellen) benutzt man einen Reflektorspiegel und ein Empfangshorn (LNB) (FB)	Abb. 15: Nahezu gleiche Abstände sorgen für eine gute Antennenverstärkung in einem kleinen Frequenzbereich (Resonanz). Damit man nicht nur einen Sender gut empfangen kann, sind die Abstände leicht unterschiedlich. Und für verschiedene Frequenzbänder benötigt man jeweils eine eigene Antenne. (FB)

Abb. 15a: Breitbandige Antennenanlage von Gigahertz bis Megahertz, Stablänge und Abstand der Stäbe entscheiden über die Empfangsfrequenz der einzelnen Antennenbereiche. (FB)

Abb. 16: Breitbandige Antenne für Frequenzen bis 2 GHz, die Länge der "Stäbe" ändert sich von etwa 10 cm bis 1 cm. (FB)	Abb. 17: Ausschnitt (FB)

Abb. 18: Ein Mikrowellen-Horn sendet gegen eine Blechwand. Die Wellen werden reflektiert. Mit der verschiebbaren Meßdiode am Stab läßt sich die Feldstärke im Zwischenraum bestimmen. (FB)	Abb. 19: Bringt man zwei parallele Metallstäbe (Lecherleitung) in das Mikrowellenfeld, so bilden sich auch hier stehende Wellen aus. Die Meßdiode ist verschiebbar. (FB)

Abb. 20: Lecherleitung im Feld von Mikrowellen. Außerhalb des Bildes: Mikrowellen-Horn (links) und Reflektor-Blechwand (rechts). (FB)

Abb. 21: Flache Antenne für Mikrowellen, Flach-Antenne für Satellitenempfang (FB)

Abb. 22: Auf dieser Teslaspule befindet sich oben ein kleiner Draht, sechs Zentimeter lang. (dahinter ein Plastiklineal als Maßstab) (FB	Abb. 23: Ist der Transformator in Betrieb, gibt es an der Spitze Büschel-Entladungen. tesla Auf dem Draht bilden sich stehende Wellen aus, die mit ihren hohen Feldstärken auch seitliche Entladungen bewirken. Wenn der Abstand dieser "Funkenringe" drei Millimeter beträgt, dann entspricht das einer Frequenz von 300.000.000/(0,003*2) 50 GigaHertz. (FB)

Abb. 24: Mit den mechanischen Schwingungen eines Piezo-Elementes lassen sich Dichteunterschiede als stehende Welle in Wasser einschreiben. Das Wasser befindet sich in der Küvette im Vordergrund. Ein Laserstrahl wird von hinten durch das Wasser gelenkt, trifft auf das periodische Dichtemuster und läßt dabei auf einem Projektionsschirm ein Beugungsbild entstehen. Debye-Sears-Effekt brechungsindex (FB)