Friedrich Balck > Biosensor > Physik > Oberton-Saite

Beobachtungen:

Obertöne einer Saite.

Was die Musikinstrumente unterscheidbar macht, ist die charakteristische Zusammensetzung deren Töne aus vielen verschiedenen Teiltönen (Obertöne). Das Klangspektrum einer gestrichenen Saite soll hier untersucht werden.
Physikalisch handelt es sich bei einer Saitenschwingung um eine stehende Welle.
Wie man ein Spektrum analysiert und welche Möglichkeiten für die Teiltöne existieren (Obertonreihe), beantwortet die Frequenzanalyse.
Etwas komplizierte Teiltonzusammensetzung findet man bei Glocken.

Beim Cello handelt es sich um System von gekoppelten Schwingungen. Die Saiten und der Resonanzkörper tauschen Energie aus.
gekoppelt

1. Töne auf einer gestrichenen Saite (Cello)

Abb. 01-01: Ein Cello, der gestrichene Bogen regt die Saiten zum Schwingen an. (FB)

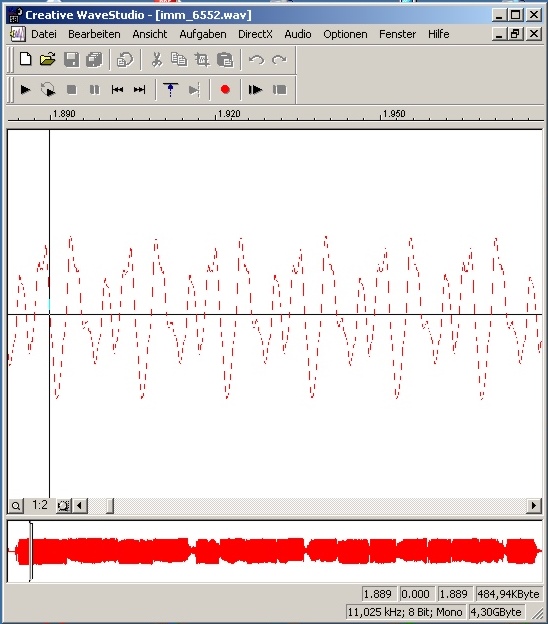Abb. 01-02:
unteres Fenster, 44 Sekunden Cello C-Saite, tiefste Saite.
aufgetragen ist das Mikrofonsignal gegen die Zeit für Grundton und verschiedene Flageolet-Töne auf dieser Saite.
oberes Fenster, Zeitausschnitt von etwa 1,89 bis 1,98 Sekunde.

Es ist kein reiner Sinuston!

Tondatei imm_6552.wav (484 kB)
(FB)

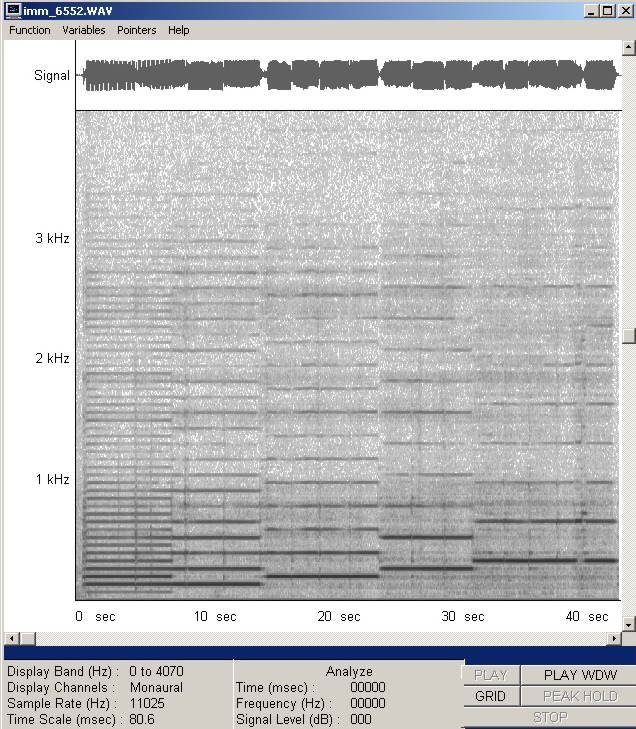Abb. 01-03: Die Cello-Saite mit etwa 64 Hz Grundfrequenz, mit dem Bogen gestrichen.
Frequenzanalyse der .WAV-Datei frequenzanalyse
Die Harmonischen reichen bis über 3200 Hz hinaus, also bis über die Nummer 3200/64 = 50.

oberes Fenster wie in Abb. 02 (Lautstärke)

Zeit: 0 -6 Sec. die Grundschwingung 64 Hz und die Reihe der Teiltöne, Vielfache von 64 Hz.

Zeit: 6-13 Sec. erster Oberton zur Grundschwingung (Oktave mit 2*64= 128 Hz ) und die Reihe der zugehörigen Obertöne, erzeugt als Flageolet-Ton, d.h. Saite bei der Hälfte etwas festgehalten, aber nicht auf das Griffbrett heruntergedrückt

Zeit: 13-24 Sec. zweiter Oberton zur Grundschwingung (Oktave + Quinte mit 3*64=196 Hz) und die Reihe der zugehörigen Obertöne, erzeugt als Flageolet-Ton, d.h. Saite bei ein Drittel festgehalten.

Zeit: 24-31 Sec. dritter Oberton zur Grundschwingung (Oktave + Oktave mit 4*64=256 Hz) und die Reihe der zugehörigen Obertöne, erzeugt als Flageolet-Ton, d.h. Saite bei ein Viertel festgehalten

Zeit: 31-40 Sec. vierter Oberton zur Grundschwingung (Oktave +Oktave +Terz mit 5*64=324 Hz) und die Reihe der zugehörigen Obertöne, erzeugt als Flageolet-Ton, d.h. Saite bei ein Fünftel festgehalten.

Offensichtlich ist jeder mit Flageolet gegriffene Ton vom Aufbau der Teiltöne her ein "selbstständiger" Ton, für den die gleichen Regeln gelten wie die für die Grundschwingung der Saite.
Die Frequenzen der Teiltöne sind ganzzahlige Vielfache von der des Grundtones. (FB)

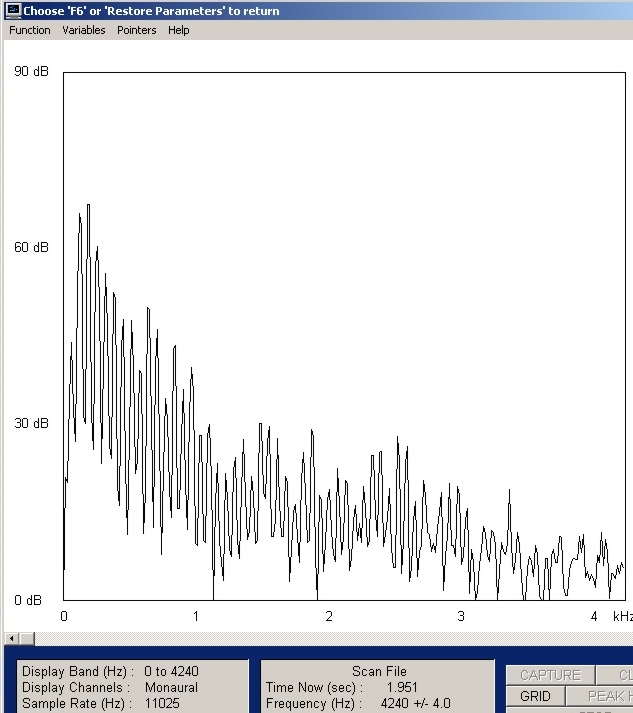Abb. 01-04: senkrechter Schnitt durch das Diagramm (Abb. 15) bei der Zeit 1,951 Sec.
Obertöne der Grundschwingung 64 Hz
Die Amplituden der Obertöne nehmen zu höheren Frequenzen ab. Die Abnahme erfolgt aber nicht nach einem einfachen Gesetz. Sondern Eigenschaft von Instrument und Spielart beeinflussen zusätzlich die Lautstärke einzelner Obertöne.
Im Bereich unmittelbar über 1000 Hz gibt es geringe Amplituden. (FB)

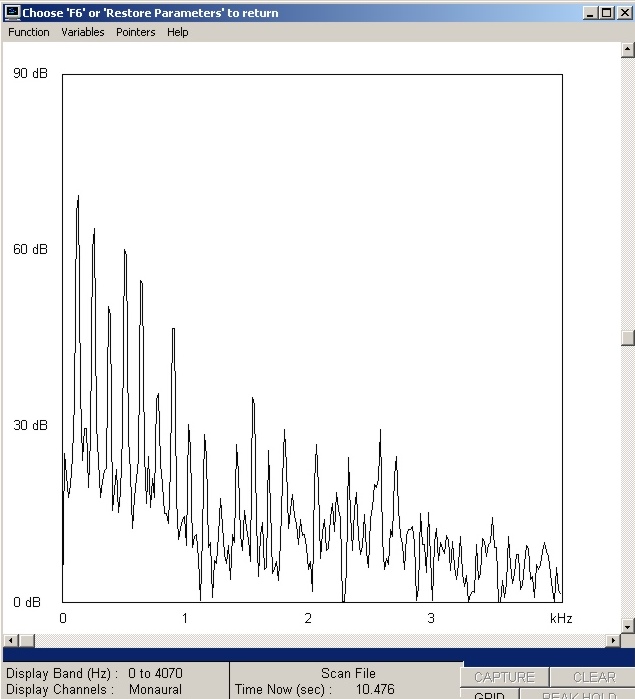Abb. 01-05: senkrechter Schnitt bei der Zeit: 10,476 s
Obertöne des ersten gegriffenen Obertones (Flageolet).2*64 Hz
Die Töne liegen jetzt doppelt so weit auseinander, die gehörte Frequenz des "Grundtones" ist eine Oktave höher.
Bei etwa 1000 Hz ist die Lautstärke geringer. (FB)

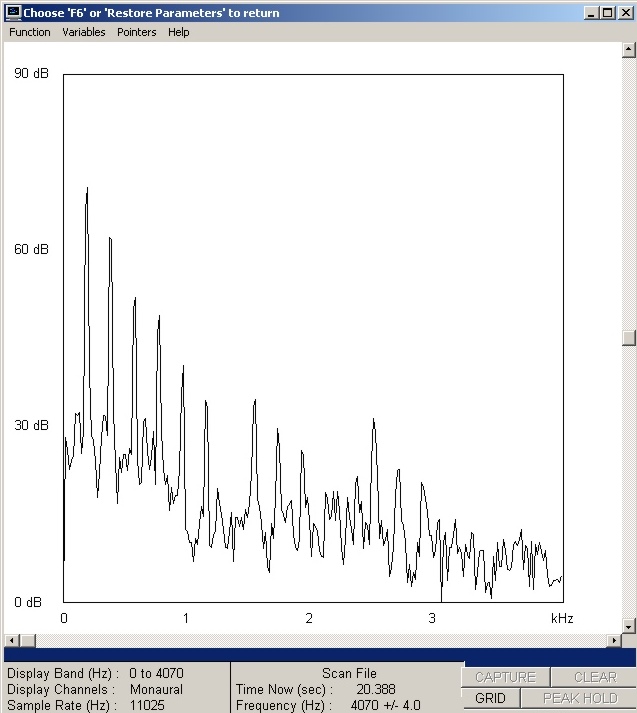Abb. 01-06: senkrechter Schnitt bei der Zeit: 20,388 s
Obertöne des zweiten gegriffenen Obertones (Flageolet). 3*64 Hz
Einige Vielfache der Grundfrequenz haben geringe Amplitude. (FB)

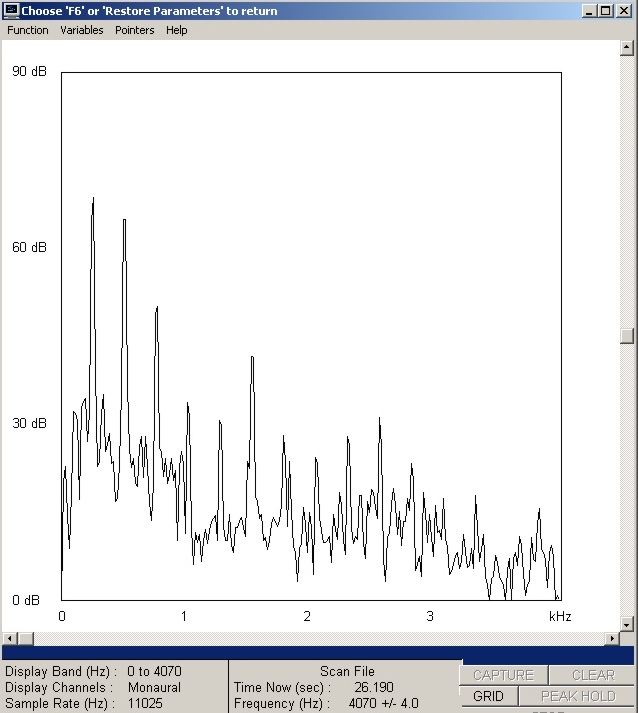Abb. 01-07: senkrechter Schnitt bei der Zeit: 26,190 s
Obertöne des dritten gegriffenen Obertones (Flageolet). 4*64Hz
Einige Vielfache der Grundfrequenz haben geringe Amplitude.(FB)

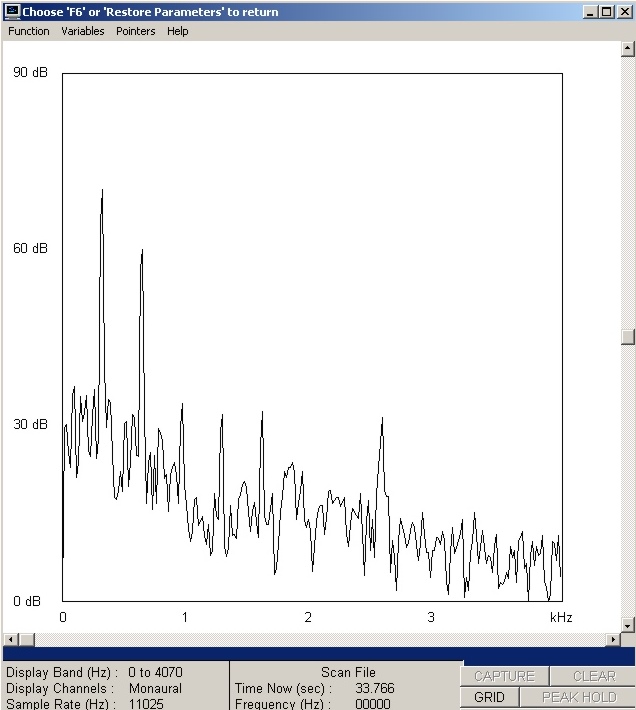Abb. 01-08: senkrechter Schnitt bei der Zeit: 33,766 s
Obertöne des vierten gegriffenen Obertones 5*64Hz (Flageolet).
Eine Teiltöne sind sehr schwach. (FB)

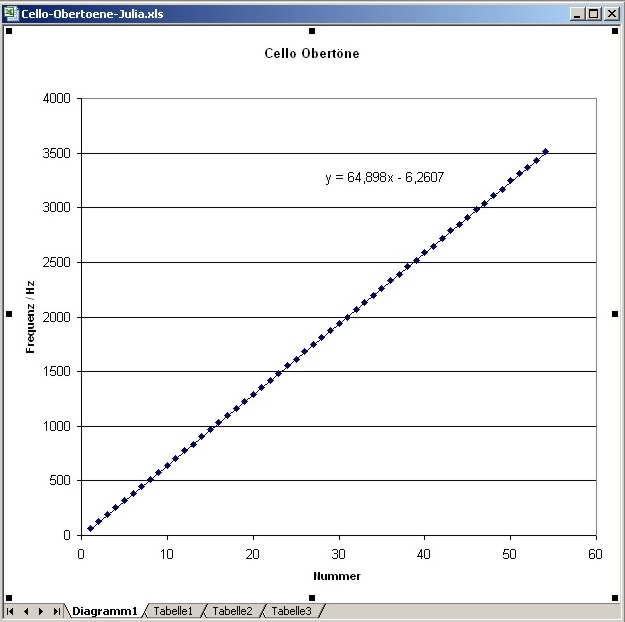Abb. 01-09: Die Frequenzen des Grundtones und der einzelnen Obertöne fortlaufend aufgetragen.
Die Ausgleichsgerade ergib eine Steigung von 64,89 Hz. Bis über den 50. Oberton hinaus bleibt der Abstand der Töne untereinander gleich. Die Saite verhält sich bei kleinen Wellenlängen immer noch wie ein loses Seil und nicht wie ein gebogener Stab.
Im Vergleich dazu die Kurve für den vielsaitigen Monochord, bei der die Saite bei kurzen Wellenlängen "härter" wird, wegen der Biegesteifigkeit des Drahtes. gekoppelt.htm#monochord Abb. 14
imm_6552.wav Cello-Obertoene-Julia.xls
(FB)

Zum Vergleich: gerechnete Dreiecksschwingung, gleiche Frequenz, symmetrisches Dreieck,
Sägezahn

siehe auch frequenz-synthese Abb. 03

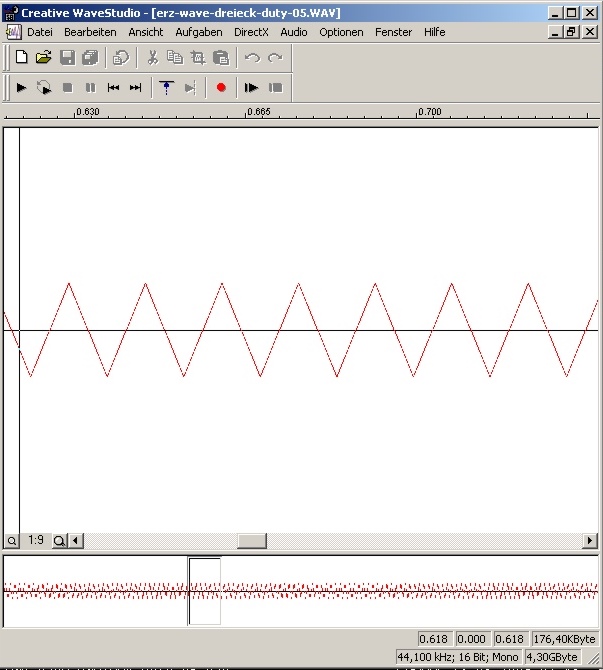Abb. 01-10: gerechnete Dreiecksschwingung. Anstiegzeit = Abfallzeit (Dutycycle= 50%) (FB)

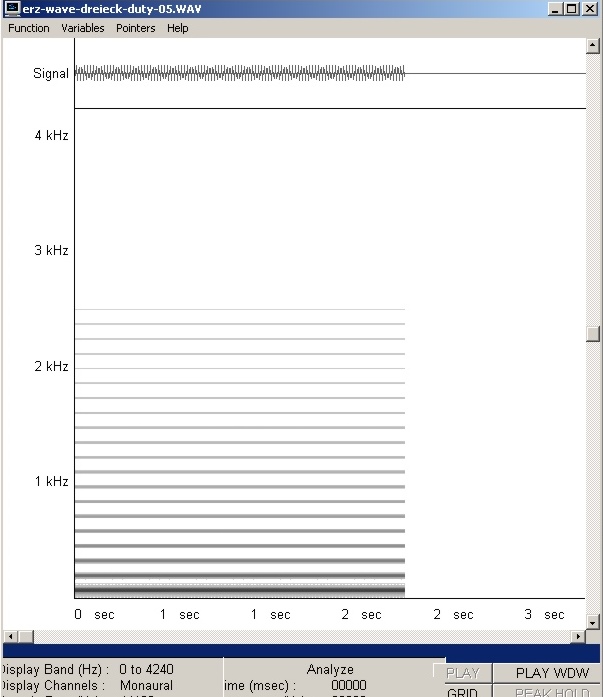Abb. 01-11: Frequenzanalyse (FB)

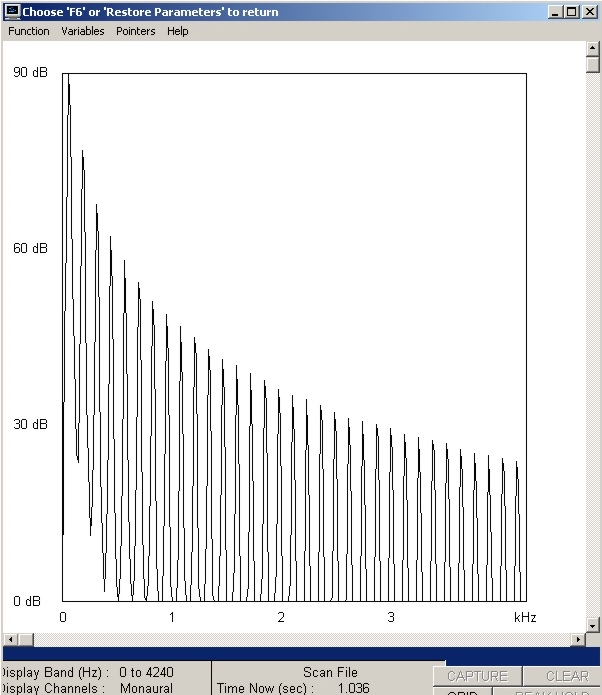Abb. 01-12: Schnitt durch Abb. 11 bei der Zeit 1,036 s. Die Amplituden der Obertöne nehmen gleichförmig ab. (FB)

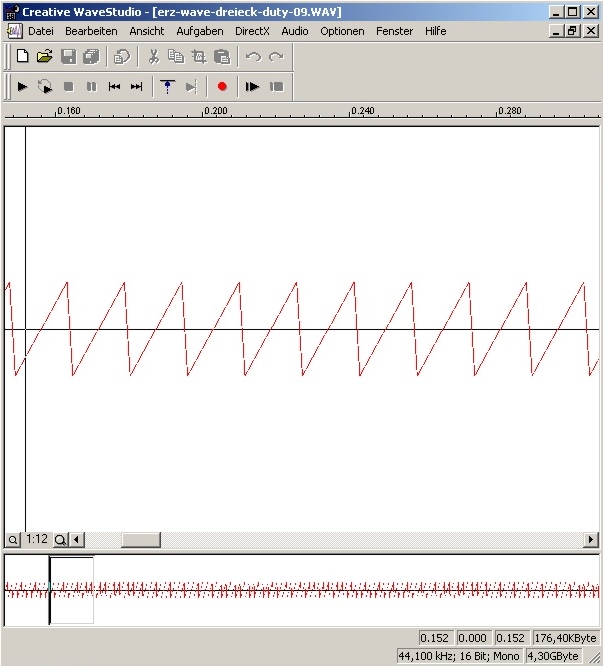Abb. 01-14: gerechnete Dreiecksschingung. Dutycycle = 90%
Die Daten enthalten möglicherweise kleinste Fehler (Rundungsfehler, Zeitraster-Einflüsse. . .), die sich in diesem Diagramm nicht aber möglicherweise in der Frequenzanalyse als Artefakte bemerkbar machen können. (ähnlich wie Moiré-Effekt moire) (FB)

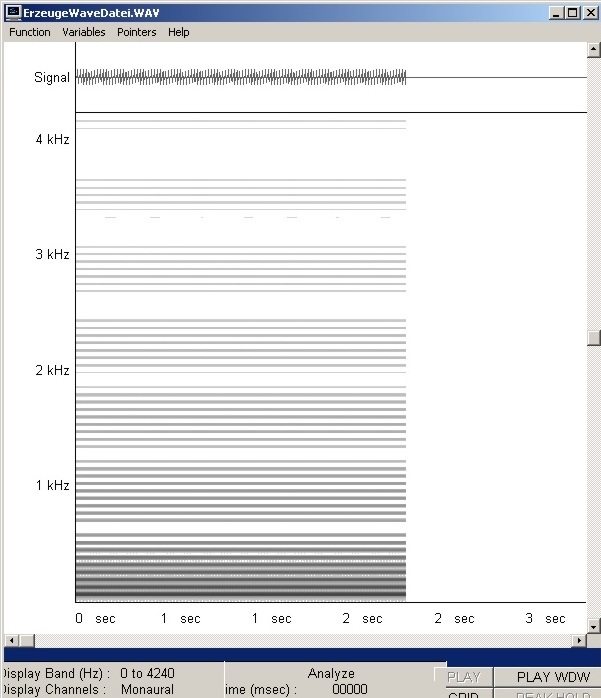Abb. 01-15: Frequenzanalyse (FB)

Abb. 01-16: Schnitt durch Abb. 15 bei der Zeit 0,986 s.
Die Amplituden der Obertöne nehmen zwar nach oben hin ab. Die Hüllkurve ist aber durch Einbuchtungen strukturiert. Einzelne Obertöne sind stark abgeschwächt. Artefakt?? (FB)

2. Physik der gestrichenen Saite

Abb. 02-01: eine Saite wird mit einem Bogen gestrichen, rechts daneben ist ein Tonabnehmer für Guitarren.
Sie wirkt wie ein elektrischer Generator (FB)

Abb. 02-02: Durch die Saite fließt ein Gleichstrom. Die Bewegung der Saite induziert im Aufnehmer eine Wechselspannung (FB)

Abb. 02-03: alternativ geht es auch so: Die Saite schwingt zwischen den Polen eine U-förmigen Magneten. Dabei entsteht an den Enden ein Wechelspannung. (wirkt als elektrischer Generator) (FB)

Abb. 02-04: Saite gezupft, Grundschwingung mit Oberwellen (FB)

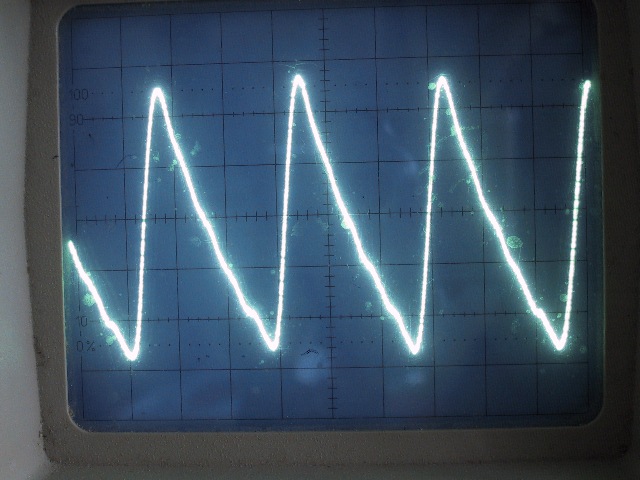Abb. 02-05: Saite mit Bogen gestrichen, Tonabnehmer in der Nähe von dem einen Ende,
Sägezahn, links steile Flanken

aus frequenz-analyse.htm
Saite ohne Resonanzkörper,
Der Kurvenverlauf ist sägezahnförmig. Beim Anstieg wird die Saite vom Bogen mitgenommen, beim Abfall schwingt sie frei zurück. Es wechseln zwei Prozesse nacheinander: zurückgleiten-festhaften = slip-stick. In der Anstiegsflanke ist mindestens eine weitere Sinusschwingung sichtbar

ausführliche Untersuchung dazu auf Seite 78
Die Physik der Musikinstrumente, Spektrum Verlag Heidelberg, 1988, ISBN 3-922508-49-9
(FB)

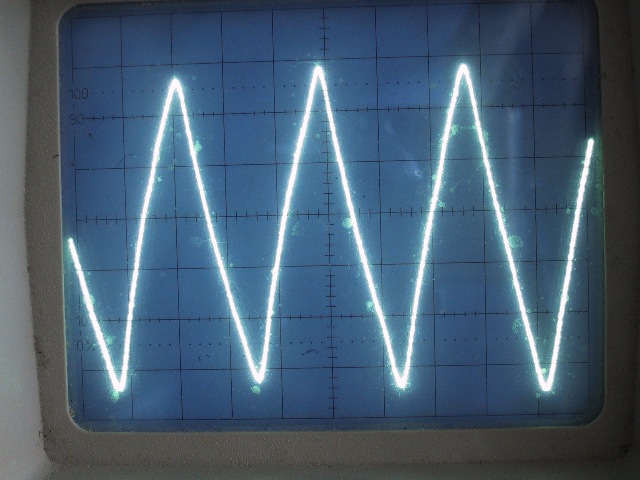Abb. 02-06: Saite gestrichen, Tonabnehmer in der Mitte der Saite
Sägezahn symmetrisch (FB)

Abb. 02-07: Saite gestrichen, Tonabnehmer am anderen Ende der Saite
Sägezahn, rechts steile Flanke (FB)

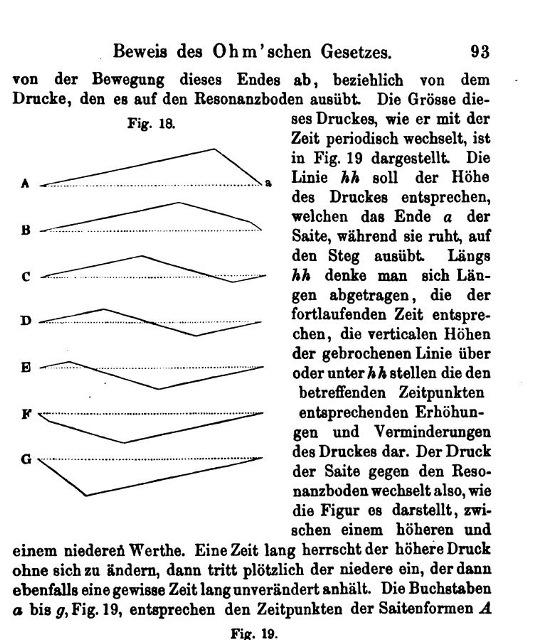
Abb. 02-08: Schwingung einer gestrichenen Saite. Es läuft ein Dreieck herum.
H. v. Helmholtz Die Lehre von den Tonempfindungen 1865 - Seite 93

Abb. 02-09: Schwingung einer gestrichenen Saite. Es läuft ein Dreieck herum.
H. v. Helmholtz Die Lehre von den Tonempfindungen 1865 - Seite 579

Abb. 02-10: Euphon nach Chladni, hier kommt bei der Tonerzeugung auch ein Slip-Stick-Mechanismus vor.
Biegebalken aus Eisen mit einem Glasrohr in der Mitte. Faßt man ein Glasrohr zwischen Daumen und Zeigefinger (angefeuchtet) und zieht es nach oben, dann entsteht ein Ton.
Bis zu einer gewissen Stärke der Haftreibung folgt das Glasrohr, dann reißt es sich los und schwingt zurück. (FB)

Abb. 02-11: Glasharfe, auch hier erzeugt man die Töne mit slip-stick Mechanismus, die Welle dreht sich und der Spieler berührt mit angefeuchteten Fingern die Gläser (FB)

Abb. 02-12: Klangschale, mit feuchten Händen wird über die Griffe gerieben. slip-stick-Mechanismus
blechblasinstrument-06.htm#kapitel-06-02a
(FB)