Beobachtungen:
Glasfaser-Feuerrad
Bei Licht nimmt man an, daß es sich um eine elektromagnetische Welle handelt.
Viele Experimente und Berechnungen zeigen, daß dieses Modell seine Berechtigung hat.
Jedoch erlaubt der Welle-Teilchen-Dualismus auch eine andere Sichtweise, nämlich:
Licht besteht aus Teilchen ("Photonen").
Die hier mit einfachsten Mitteln durchgeführten Experimente bestätigen das Auftreten von Teilchen.
Bewegte Materie ist an ihren Spuren in der Umgebung zu erkennen.
Die Spuren von Licht in einer Glasfaser sind ähnlich wie die von
- fließendem Wasser im Rohr,
- Luftströmung im Rohr,
- elektrischem Strom im Draht.
Die hier beschriebenen Experimente sind völlig neuartig!
Passend dazu:
- Ein sehr kurzer Witz: " Es treffen sich zwei Jäger. "
- Beim LHC- Beschleuniger in Genf schießt man Teilchen mit großer Energie aufeinander und untersucht
die Spuren in der Nähe von dem "Treffpunkt".
Was passiert, wenn zwei Lichtstrahlen aufeinander treffen?
- Mit Hilfe einer Glasfaser läßt sich ein sehr einfaches Experiment durchführen. Man kopple an beiden Enden der Faser Licht ein.
- Während man beim Beschleuniger die Teilchenstrahlen mit aufwendigen und teuren Methoden (Magnetfeldern) auf ihren Bahnen hält, bietet eine Lichtleitfaser schon für ca. 1 Euro pro Meter auch gute Strahlführungsbedingungen.
- Lichtleitfasern mit optischen Verlusten sind für das Experiment hervorragend geeignet, da die Strahlintensität entlang der Faser ständig abnimmt.
- Sensitive Personen können feinstoffliche Strukturen außerhalb der Faser wahrnehmen, obwohl die Ummantelung der Faser kein Licht nach draußen gehen läßt.
- Die geometrische Ausdehnung dieser Strukturen hängt von der Lichtintensität in der Faser ab.
- Durch einfaches Abmessen von Längen erhält man Informationen über das Licht in der Faser.
- Weiterhin ist mit der bewegten Materie eine Richtungsinformation gekoppelt, so daß man einen
Richtungswechsel des Lichtes in der Faser von außen lokalisieren kann.
- Zunächst beobachte man die Lichtintensität entlang der Faser bei nur einer Lichtquelle in Abhängigkeit
von deren Einstrahlung. Damit erhält man auch ein Maß für die optischen Verluste. - Anschließend schalte man die zweite Lichtquelle am anderen Ende dazu. Bei gleichen Einstrahlungen sollte der Treffpunkt in der Mitte der Faser zu beobachten sein. Der Treffpunkt ist dort, wo die Einstrahlungen von beiden Enden gleich groß sind. Bei unterschiedlichen Verhältnissen sollte sich der Treffpunkt zur schwächeren Quelle hin verschieben. Hierbei spielt die Abnahme der Intensität mit der Länge der Faser wegen der optischen Verluste eine entscheidende Rolle.
- Die Intensität in einer Faser nimmt mit deren Länge ab.
- Bei Einstrahlung von beiden Enden aus hängt die Lage des Treffpunktes
vom Verhältnis der Stärke beider Lichtquellen ab. - Die mit dieser Methode ermittelten optischen Verluste (Dämpfung in dB/km)
stimmen größenordnungsmäßig mit den Herstellerangaben zur Faser überein.
Dies wurde an einer Monomode-Faser aus Quarz und einer Polymerfaser getestet. - Das Experiment bestätigt, daß bei Licht in einer Faser Teilchen beteiligt sind.
0. Einleitung
0.1 Vorarbeiten, Versuch vom Juli 2018
0.2 Fettfleck-Photometer nach Robert Bunsen
0.3 Berechnung der Dämpfung bei Fasern
1. Versuche mit Lichtleitern: An beiden Enden wird Licht eingespeist
2. Bestimmung der materialspezifischen Dämpfung
3. Fortgeschrittene Experimente, Fasern und Sonnenlicht
4. Experimente mit Bündeln aus Sonnenlicht
0. Einleitung
0.1 Vorarbeiten, Versuch vom Juli 2018
Sie sind in TEIL-5 beschrieben :
wbm-2018-teil05a-high.pdf
Seite 7
 |
| Abb. 00-01: Ein Wasserschlauch ist ausgelegt. Wenn Wasser fließt sind parallel dazu auf beiden Seiten drei Streifen spürbar. wbm-2018-teil05a-high.pdf |
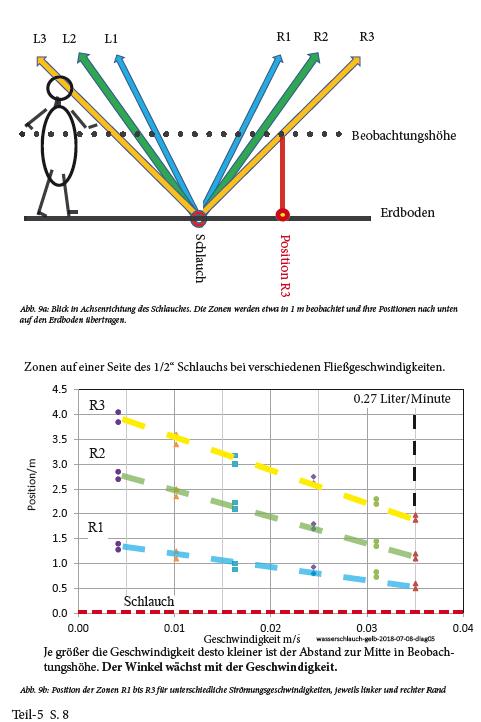 |
Abb. 00-02: Die Abstände der Streifen zum Schlauch werden bei kleinerer Geschwindigkeit (geringerer Durchfluß) größer. wbm-2018-teil05a-high.pdf |
 |
| Abb. 00-03: Auch bei einem Lichtleiter erzeugt eingespeistes Licht ähnliche Streifenstrukturen. wbm-2018-teil05a-high.pdf |
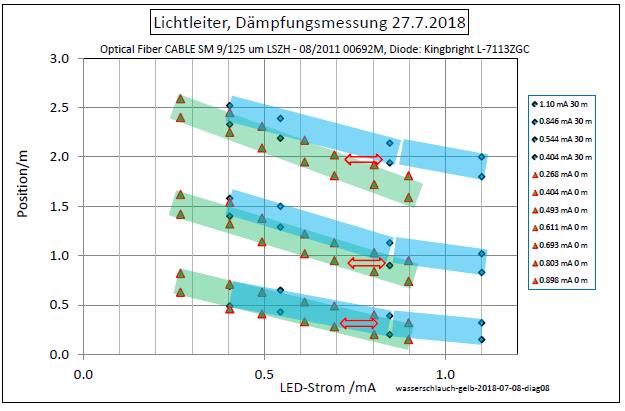 |
Abb. 00-04:aus wasser-ader-zwei.htm#kapitel-09-02Die Abstände der Streifen sind ein Maß für den Durchfluß (s.o) Da die Intensität des Lichtes in der Faser gedämpft wird, ist eine kontinuierliche Änderung der Abstände entlang der Faser zu beobachten. Aus den gemessenen Abstände läßt sich somit berührungslos auf die Abnahme der Lichtintensität in Faser (Dämpfung) schließen. Hierzu braucht man nur die Maße an zwei unterschiedlichen Stellen der Faser und die relative Abhängigkeit der Maße vom Diodenstrom. zum Diagramm: Strukturen parallel zur Faser, die Beleuchtung kam von einer grünen LED, 520 nm rot: bei der Referenzlänge 0 m, blau: 30 m weiter Bei diesen Strömen haben die Gruppen mit den drei Streifen jeweils ähnliche Abstände zur Faser. Die Ströme unterscheiden sich (rote Pfeile, grob geschätzt!) um den Faktor 0.8/0.7 = 1.14, d.h. die Dämpfung bei 30 m Faser läßt sich mit einer Stromerhöhung von 1.14 kompensieren. Damit ergibt sich für die Materialeigenschaft: Dämpfung in dB: 10 log(1.14) = 0.579 dB pro 30 m also pro Meter 0.579/30 dB/m = 0.0193 dB/m oder 19 dB/km Annahme: Die Lichtleistung ist proprotional zum Diodenstrom. Daher wurde nicht mit 20 log (1.14) gerechnet. Denn bei einer LED ist die Leistung proportional zum Diodenstrom, da die Diodenspannung nahezu konstant bleibt! (FB) |
Angaben in der Literatur
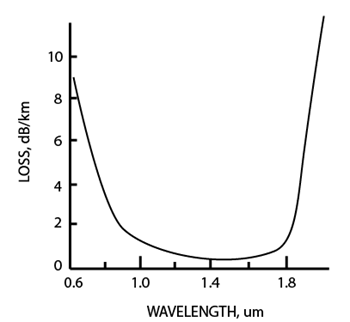 |
| Abb. 00-05: Bei Monomodefasern gibt es Angaben für die Wellenlänge im Infraroten (1310nm): etwa 1 dB / km https://de.wikipedia.org/wiki/Lichtwellenleiter Im Sichtbaren (z.B. 520 nm) werden die Fasern praktisch nicht eingesetzt, da der Verlust zu hoch ist. Denn bei kleinen Wellenlängen im Vergleich zum Infraroten steigt der Verlust durch Streuung mit der vierten Potenz an. "The attenuation of the optical fiber is a result of two factors, absorption and scattering. The absorption is caused by the absorption of the light and conversion to heat by molecules in the glass. Primary absorbers are residual OH+ and dopants used to modify the refractive index of the glass. This absorption occurs at discrete wavelengths, determined by the elements absorbing the light. The OH+ absorption is predominant, and occurs most strongly around 1000 nm, 1400 nm and above1600 nm."https://s3-us-west-1.amazonaws.com/foscoshopify/graphics/uploads/2010/09/image_thumb26.png |
0.2 Fettfleck-Photometer nach Robert Bunsen
Licht fällt von zwei Seiten auf einen Fettfleck
"Der Versuchsaufbau besteht aus zwei Lichtquellen. Dazwischen ist ein Blatt Papier mit einem Fettfleck.
Anfangs erscheint der Fettfleck entweder heller oder dunkler als das umgebende Papier, da fettiges Papier das Licht schlecht reflektiert, aber relativ viel Licht durchlässt. Man verschiebt nun das Blatt solange, bis der Fettfleck zu verschwinden scheint. Dann gilt für die Lichtstärken I1 und I2 und die Abstände R1 und R2 jeweils von der Lichtquelle bis zum Papier"
I1 / I2 = R12 / R22
(in Anlehnung an https://de.wikipedia.org/wiki/Fettfleck-Photometer)
Lichtstärke: in den Raumwinkel abgestrahlter Lichtstrom
Mit zunehmendem Abstand zur Lichtquelle R wächst die vom Raumwinkel abgegrenzte beleuchtete Fläche an.
Diese ist proportional zum Quadrat des Abstandes (R2).
Leuchtdichte: von einer Fläche ausgehende . . . . .. , Helligkeitseindruck des Auges
 |
| Abb. 00-06: Zwei Lichtquellen und ein Blatt Papier mit einem Fettfleck (Öltropfen) Dort, wo die Helligkeiten auf der Vorder- und Rückseite gleich sind, gibt es nur einen schwachen Kontrast zwischen Papier und Fettfleck. (FB) |
   |
| Abb. 00-07: links: Das Papier ist dicht vor der linken Lampe, der Fleck erscheint hell, Mitte: etwa in der Mitte, der Fleck ist kaum zu sehen, rechts: dichter vor der rechten Lampe, der Fleck erscheint dunkel. |
Zwei Scheinwerfer strahlen gegeneinander
 |
| Abb. 00-08: Zwei Scheinwerfer (punktförmige Lichtquelle mit Linsenoptik) sollen eine kegelförmige Abstrahlung haben. Die vom Kegel ausgeleuchtete Fläche wächst quadratisch mit dem Abstand, daher verringert sich die Lichtstärke entsprechend. Wenn beide Lampen gleichstark leuchten, dann befindet sich der Ort mit gleicher Lichtstärke genau in der Mitte (R1 = R2) . Auf die kreisförmige Schnittfläche in der Mitte fällt dann gleichviel Licht von beiden Seiten (I1 = I2) (FB) |
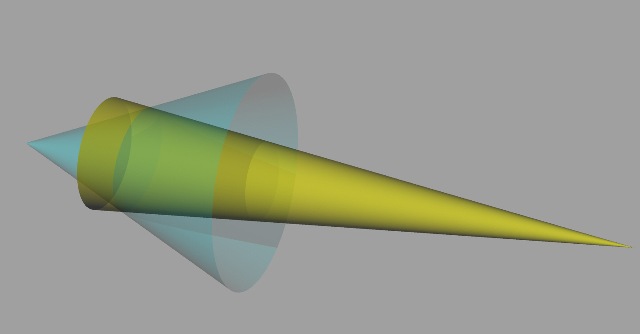 |
| Abb. 00-09: Wird die Leuchtdichte der linken Lampe verringert z.B. durch Reduzierung des Stromes, muß man, um den gleichgroßen Lichtstrom auf der Fläche zu halten, den Abstand verkleinern und auch den Öffnungswinkel vergrößern. (FB) |
0.3 Berechnung der Dämpfung bei Fasern
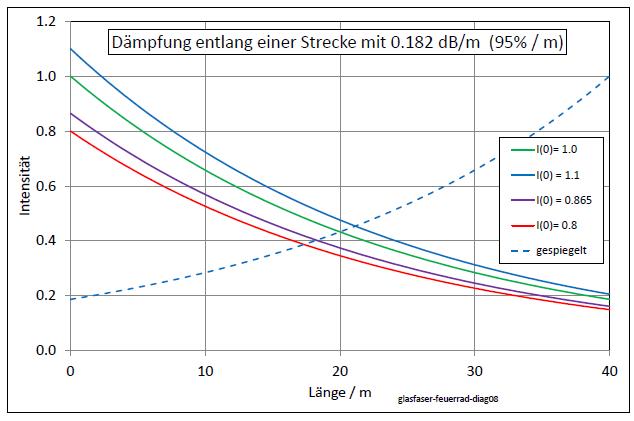 |
| Abb. 00-10: Die lokale Intensität in einer Glasfaser hängt von der Anfangsintensität I(0) und von der Entfernung zur Lichtquelle ("Länge") ab. Bei diesem Bespiel wird mit einer in der Praxis vorkommenden Materialeigenschaft für die Dämpfung 182 dB/km und für um wenige Prozente abweichende Anfangsintensitäten gerechnet : I(0) = 1 ; 1,1 ; 0.865; und 0.8 (Der Wert 0.865 wird bei den folgenden Experimenten gebraucht) Bei der gestrichelten Kurve handelt es sich um die Anordnung, bei der die Einspeisung des Lichtes vom anderen Ende angenommen wird (grüne Kurve gespiegelt). (FB) |
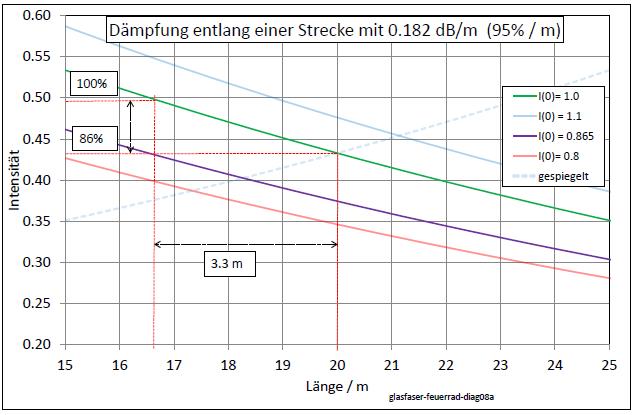 |
| Abb. 00-11: (Auschnitt) Für die nachfolgenden Exerimente wird gebraucht, wie sich die Intensität im Bereich von wenigen Metern ändert. Die Antwort läßt sich durch Berechnung ermitteln. Ausgehend von der Mitte der Faser, dort wo sich die grüne und die gestrichelte Kurve schneiden, wird gefragt, um wieviel man die Anfangsintensität vergrößern muß, wenn man einige Meter weiter in Richtung Lichtquelle die gleiche Intensität wie vorher am Startpunkt haben will. Ergebnis: bei 3.3 Meter muß man die Anfangsintensität auf 86 % reduzieren. (lila Kurve) (FB) |
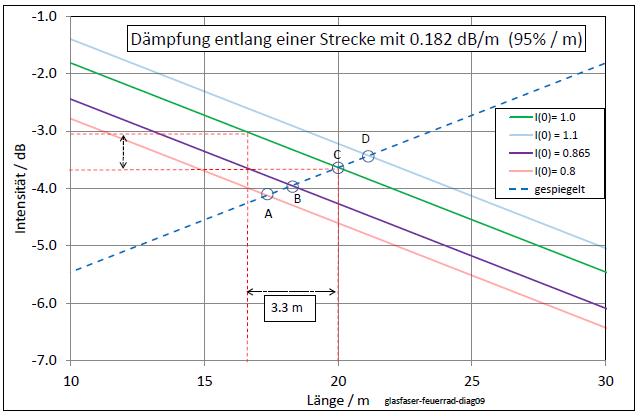 |
| Abb. 00-12: Der gleiche Datensatz in halblogarithmischer Darstellung: Der Strecke von 3.3 m entsprechen etwa 0.6 dB (3.3m * 0.182dB/m = 0.6 dB) Bei den nachfolgenden Experimenten wird gebraucht, wie sich die Schnittpunkte der Kurven mit denen der gestrichelten Kurve verschieben, wenn die Anfangsintensität geändert wird. Bei den Punkten A, B, C und D liegt die Verschiebung im Bereich von 4 Metern, wenn sich die Intensität um rund 30% ändert. Der Schnittpunkt verschiebt sich dabei von der Position C zur Position B. Die Entfernung ist die Hälfte von 3.3 m. (Strahlensatz) (FB) |
1. Versuche mit Lichtleitern: An beiden Enden wird Licht eingespeist
Aufbau
 |
| Abb. 01-01: Neben einem Teil der 50 m langen Monomode Glasfaser (gelb) liegt links ein Maßband. wasser-ader-zwei.htm#kapitel-09-02 Die Faserenden gehen in einem weiten Bogen in das Haus hinein, wo sie von beiden Enden beleuchtet werden. Außerhalb dieses geraden Stücks der Faser gibt es Strukturen, deren Position vom Verhältnis der Lichtstärken (eingestellt über die Ströme in den LEDs) abhängt. Mit den Holzstäben sind drei Gebiete mit solchen Strukturen bei unterschiedliche Strömen ausgelegt. (FB) |
 |
| Abb. 01-02: Zunächst gingen die Faserenden in einem großen Bogen bis ins Haus. (FB) |
 |
| Abb. 01-03: Die grünen LEDs stecken in Aluminiumhülsen, passend für die Faserenden (FB) |
 |
| Abb. 01-04: ummanteltes Faserende mit 2,5 mm Durchmesser (Ferrule) (FB) |
 |
| Abb. 01-05: POF, PolymerFaser (Kunststoff) Diese Faser ist 40 m lang, davon liegen 20 m parallel zum Maßband. Die restlichen Längen gehen in einem Bogen bis zum Haus. (FB) |
 |
| Abb. 01-06: Noch gingen die Faserenden in einem großen Bogen bis vor das Haus. Oben sieht man die Anschlüsse und die Gehäuse mit den beiden 660 nm LEDs. Über die Widerstandsketten ließen sich die Diodenströme präzise einstellen. Die Ströme waren in der Größenordnung von 1 mA. (FB) |
 |
| Abb. 01-07: Jedes Faserende bekommt eine eigene Stromquelle mit einem Transistor als Stromkonstanter. Auf einer von beiden Schaltung ist ein Potentiometer zur Feineinstellung des Stromes vorhanden. (FB) |
 |
| Abb. 01-08: Rote LED für die Faser, gelbe LED für den Stromkonstanter (FB) |
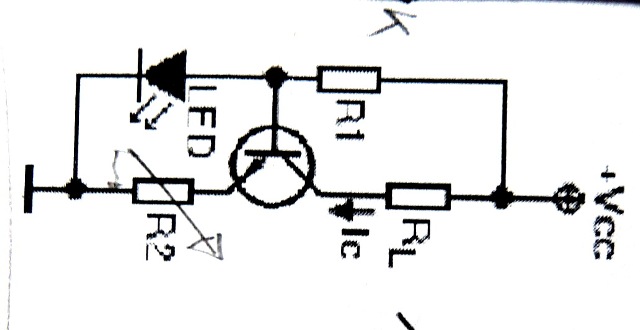 |
| Abb. 01-09: Stromkonstanter: LED, Transistor BC547, R1=3k9, R2 = 1K + 500k (Poti), RL = Last ( Diode) U= 12 V, andere Schaltung: R2 = 1.2K (FB) |
Beobachtungen
Wenn Licht von beiden Seiten in die Faser eingespeist wird, dann läßt sich von beiden Enden aus der Weg des Lichtes über die spürbaren Strukturen außerhalb der Faser verfolgen. wasser-ader-zwei.htm#kapitel-09-02
Es gibt jeweils eine spürbare Richtung "kommt mir entgegen" bzw. "geht mit mir mit", wenn man sich entlang der Faser bewegt.
Wenn beide Diodenströme nahezu gleich sind, dann gibt es etwa auf halber Strecke,
d.h. in der Mitte der Faser, einen Umschlagpunkt, bei dem die spürbare Richtung wechselt.
Verändert man einen der Ströme, so verschiebt sich diese Stelle.
Wird der Strom auf der einen Seite erhöht, wächst die Lichtstärke in diesem Faserende an und die Strecke bis zum Umschlagpunkt wird länger. Der stärkere Lichtstrahl verdrängt sozusagen den schwächeren.
Analoges Verhalten wurde schon bei früheren Experimenten als Feuerrad beschrieben. strom-sehen-009.htm
Es ist bei "Strömungen" aus Batterien, Magneten usw. zu beobachten.
 |
Abb. 01-10: Zwei Wasserstrahlen treffen aufeinander.aus bbewegte-materie.htm#kapitel-03-03 |
 |
Abb. 01-10a: Zwei Gasflammen treffen aufeinander.aus bbewegte-materie.htm#kapitel-03-03 |
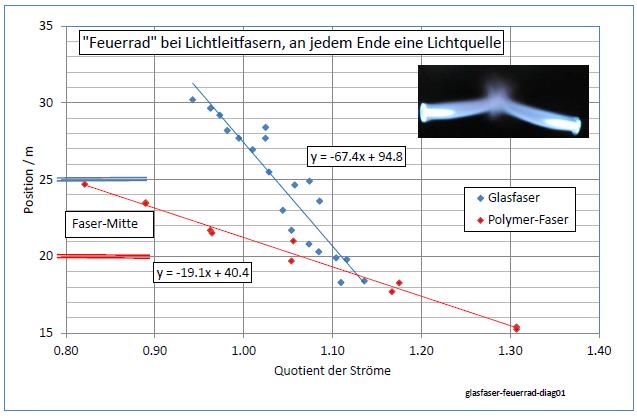 |
| Abb. 01-10b: Foto aus strom-sehen-009.htm rot: 50 m Glasfaser, erste Versuche. Trotz der Streuung der Werte gibt es eine klare Tendenz: Der Umschlagpunkt läßt sich durch Ändern eines Diodenstromes verschieben und zwar um 1,91 m pro 10% Änderung (Steigung der roten Kurve). Er stellt sich genau in der Mitte der Faser (25m) ein, wenn der eine Strom um den Faktor 1.02 größer ist als der andere. blau: 40 m PolymerFaser. Hier ist die Mitte der Faser bei 20 m. Der Umschlagpunkt läßt sich durch Änderung des Diodenstroms verschieben und zwar um 6,74 m pro 10% Änderung (Steigung der blauen Kurve). Er stellt sich genau in der Mitte der Faser (20m) ein, wenn der eine Strom um den Faktor 1.05 größer ist als der andere. Ein Grund für die Unsymmetrie kann die unterschiedliche Einkopplung des Lichtes in die Faser sein. Die Ströme für gleiche Bedingungen waren jeweils in der Nähe von rund 1 mA. Beide Trendlinien weisen unterschiedliche Steigungen auf. Bei Glas ist sie -67 m und bei POF -19 m. Die Unterschiede ergeben sich aus der unterschiedlichen materialspezifischen Dämpfung beider Fasern. Dies bedeutet, daß man bei Glas die siebenfache Strecke für die gleiche Dämpfung braucht. (Faktor 67/19= 3.5 und Faktor 2 für den Strahlensatz in Abb. 00-07 ergibt 7)) Daraus folgt, daß das Glas 1/7 der Dämpfung von Kunststoff hat. (siehe unten: Kunststoff 180 dB/km davon 1/7 ergibt 25 dB/km ) Abgeschätzt aus den Versuchen vom Juli 2018 (s.o., Abb. 00-04) ergaben sich 19 dB/km. (FB) |
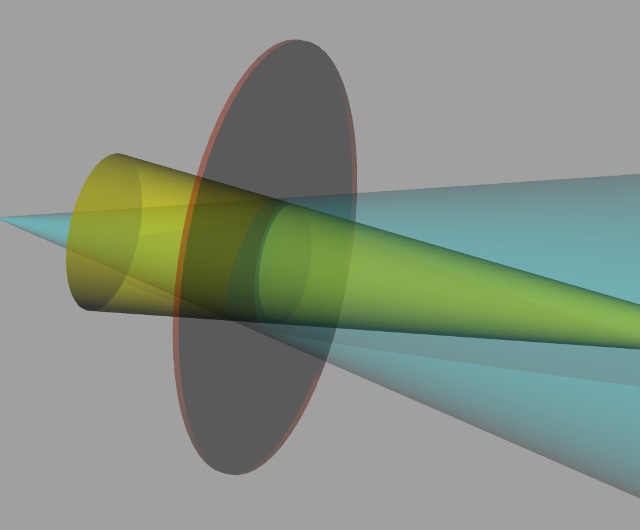 |
| Abb. 01-11: Form der Strukturen (schematisch): Wie in den Versuchen vom Juli 2018 findet man auf beiden Seiten der Faser drei etwa 20 cm breite Streifen, links L3, L2, L1 und symmetrisch dazu rechts R1, R2 und R3. Es könnte sich dabei um konzentrische Kegel handeln. Für die Bedingung, daß von beiden Seiten Licht in die Faser gegeben wird, würden sich zwei solcher Kegelsysteme überlagern. Es gibt neben der Richtungsänderung noch ein weiteres charakteristisches Merkmal für den Umschlagpunkt: dies sind zwei scheibenförmige Elemente senkrecht zur Faser mit Radius von ungefähr vier Metern. Ihr Abstand voneinander beträgt einige Zentimeter. (FB) |
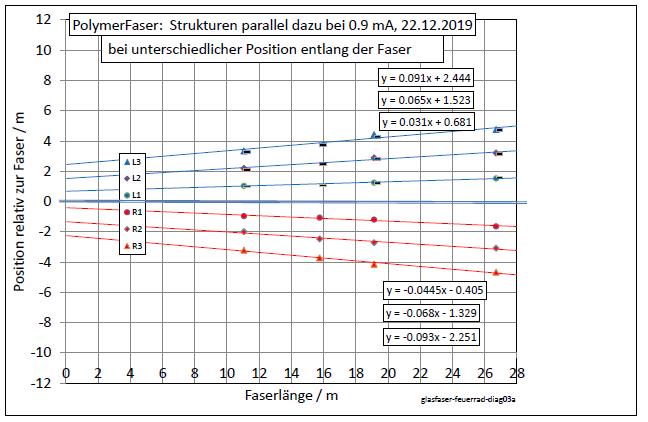 |
| Abb. 01-12: Die Strukturen entfernen sich von der Faser mit zunehmendem Abstand zur LED. (FB) |
 |
| Abb. 01-13: Sie sind symmetrisch angeordnet (schwarze Striche: Mittelwert der Abstände) (FB) |
 |
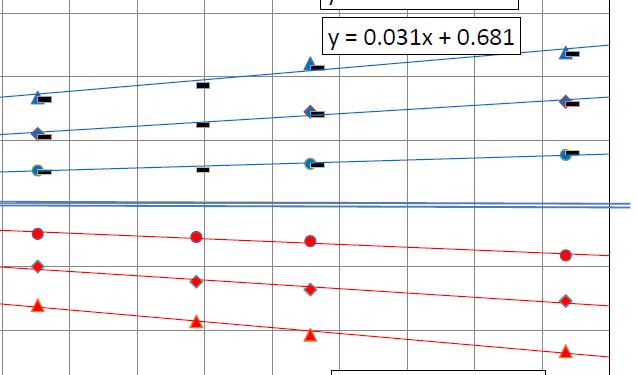
| Abb. 01-14: Zur Form der drei "Kegel" Frage: wie hängt der Öffnungswinkel von der Länge ab? linear oder quadratisch? Kurven L3R3 (Rohdaten), QL3R3 ( Quadrat der Radien) Beide Systeme der Trendlinien helfen nicht weiter. Im Nahbereich der Einspeisung fehlen noch Daten. (FB) |
 |
| Abb. 01-15: Markierungen jeweils für zwei unterschiedliche Einstellungen. Die Strukturen haben eine Breite von etwa 0.2 m (wie schon in der Versuchen von 2018 gezeigt) (FB) |
 |
| Abb. 01-16: Verlauf der Strukturen R1, R2, R3 von der Einspeisung (oben) bis zur Länge 17 m. links ist die Faser mit dem Maßband (FB) |
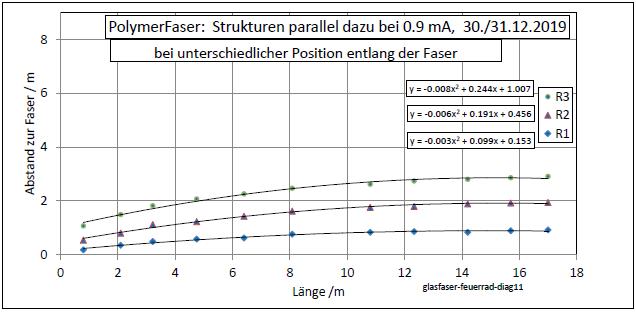 |
| Abb. 01-17: Mehr Daten, feinere Auflösung, die Diode ist links im Ursprung der Grafik. Aber auch hier bleibt die Situation in der Umgebung der Diode noch ungeklärt. (FB) |
 |
| Abb. 01-18: Idee für die Form mit geschlossenen Körpern (schematisch). Die Wände haben eine Dicke von 20 cm. (FB) |
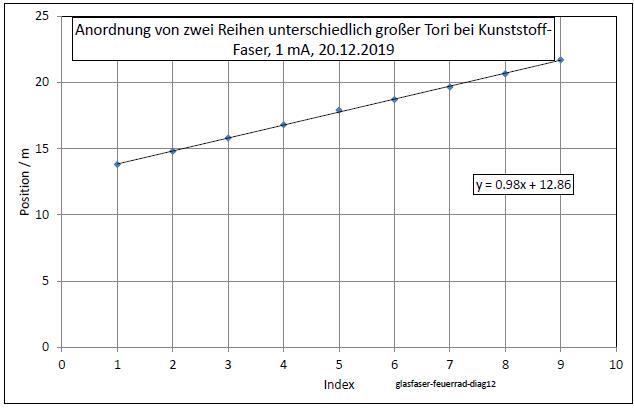 |
| Abb. 01-19: Entlang der Glasfaser gibt es zwei konzentrische Reihen von torusartigen Strukturen. Die Abstände der inneren Tori sind etwa 1 m (FB) |
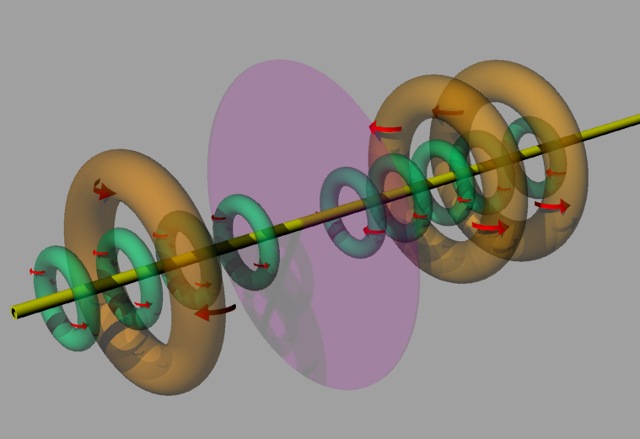 |
| Abb. 01-20: Lichtleiter und Tori im Bereich der Trennstelle (violett) (schematisch) Es gibt zwei Reihen mit unterschiedlichen Maßen. Die innere Gruppe hat einen Radius von etwa 1 m, die äußere von etwa 2.5 m. Innere und äußere haben jeweils entgegengesetzte Drehrichtungen, die sich auf der anderen Seite der Trennstelle spiegelbildlich verhalten. (FB) |
Einspeisung von Sonnenlicht in beide Faserenden
22.01.2020
 |
| Abb. 01-20a: Die beiden Enden einer Faser sind nahezu parallel zur Sonnenstrahlung ausgerichtet. Die untere Faser zeigt weniger genau auf die Sonne. Der "Treffpunkt" ist einige Meter von der Mitte der Faser entfernt. Geringfügiges Schwenken der beiden mechanisch gekoppelten Stecker im Vergleich zur Richtung der Sonnenstrahlen verändert das Verhältnis der jeweiligen Einstrahlung in die Faserenden. Damit läßt sich der "Treffpunkt" verschieben. (FB) |
Einspeisung von Sonnenlicht in beide Faserenden
22.03.2020
Auch bei Einstrahlung von Sonnenlicht in beide Enden gibt es ein "Feuerrad".
Durch unterschiedliche Justierung zur Sonnenrichtung, läßt sich das Verhältnis der Einstrahlungen verändern.
Dabei hat sich gezeigt, daß man mit unterschiedlichen Einstrahlungen die Position des Feuerrades verschieben kann, so wie es bei dem Licht aus LEDs zu beobachten war.
 |
| Abb. 01-21: Auf einem Theodolit sind beide Faserenden befestigt. Über zwei Feintriebe (horizontal und vertikal) läßt sich deren Ausrichtung zur Sonne präzise verstellen. Am Schatten an den Seiten des U-förmigen Halters kann man die Veränderungen der Einstellung beobachten. (FB) |
 |
| Abb. 01-22: U-Förmiger Halter mit beiden Faserenden. Sie sind absichtlich gegeneinander verkippt. So läßt sich mal die eine Faser oder die andere exakt auf die Sonne ausrichten. (FB) |
 |
| Abb. 01-23: die beiden Faserenden (FB) |
2. Bestimmung der materialspezifischen Dämpfung
Beleuchtung nur von einem Ende aus
 |
| Abb. 02-01: Die Einspeisung befindet sich in der oberen Bildmitte (weiße Box). Ausgelegt sind die Strukturen (links) L3 L2 L1 und (rechts) R1 R2 R3. Quer zum Maßband entlang der Faser liegen vier weitere Maßbänder zum Ausmessen der Strukturen. (FB) |
 |
| Abb. 02-02: Foto mit besserer Auflösung (FB) |
 |
| Abb. 02-03: Blechmarken mit Drahtfuß für die Bereiche L2, L1, R1, R2, R3, jeweils für beide Ränder eines Streifens bei zwei unterschiedlichen Bedingungen. (FB) |
 |
| Abb. 02-04: Blechmarken mit Drahtfuß für die Bereiche L3, L2, L1, R1, R2, R3 Bedingung 1: Draht nach links: 20.0 m, 1.0 mA sowie 16.5 m 0,865 mA Bedingung 2: Draht nach rechts: 16.5 m, 1.0 mA (FB) |
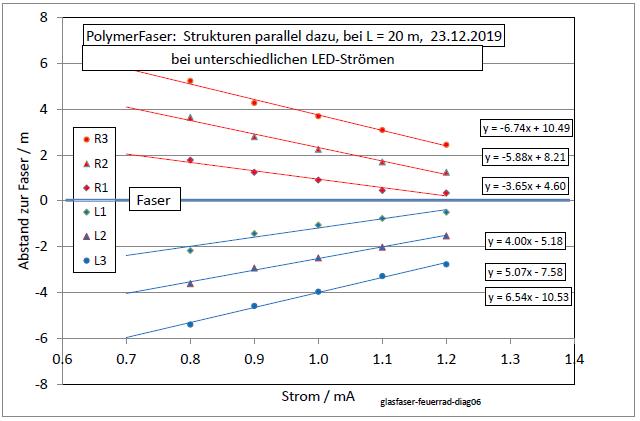 |
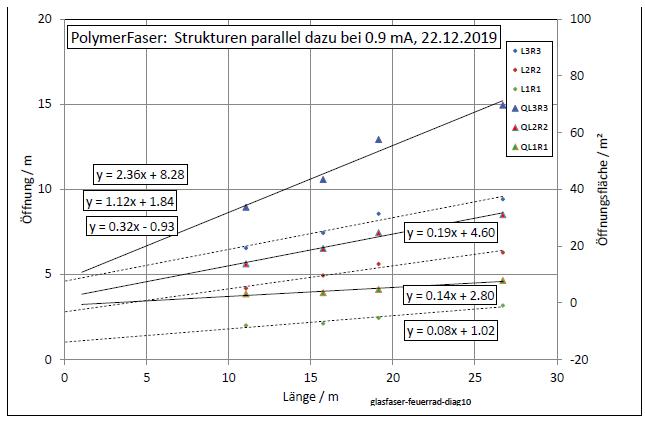
| Abb. 02-05: wie in wasser-ader-zwei.htm#kapitel-09-02 beschrieben, wurden die Streifen links (L3 L2 L1) und rechts (R1 R2 R3) aufgespürt, markiert und deren Abstand zur Faser eingemessen. Für die Mitte der Faser (20m) sind deren Positionen als Funktion des Diodenstromes aufgetragen. Die Koeffizienten der jeweiligen Trendlinien sind rechts aufgelistet. (FB) |
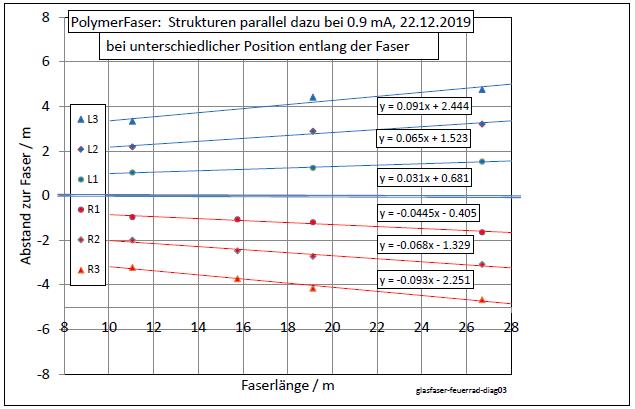 |
| Abb. 02-06: Entsprechend zeigen diese Daten die Positionen entlang der Faser bei konstantem Strom von 0,9 mA. (FB) |
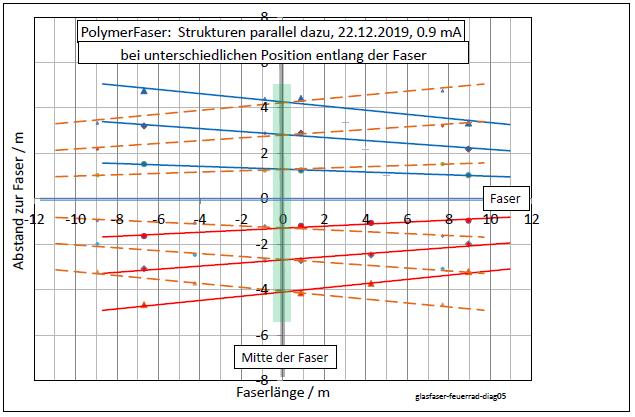 |
| Abb. 02-07: Simulation bei Beleuchtung von beiden Enden mit exakt gleichen Diodenströmen durch Überlagerung der Strukturen gestrichelt: Daten von Abb. 02-06 durchgezogen: die gleichen Daten aber gespiegelt. (FB) |
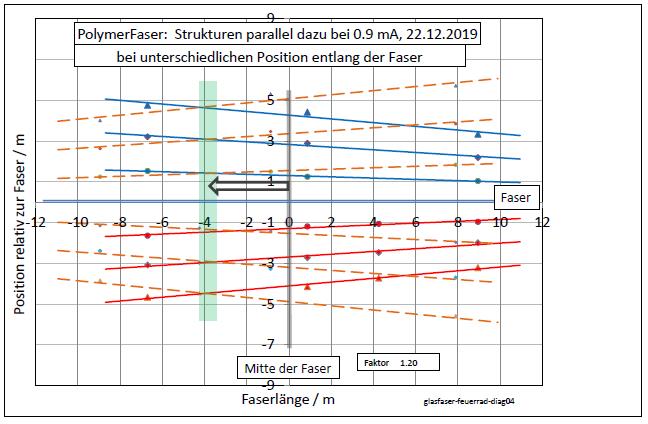 |
| Abb. 02-08: Die Diodenstrom auf der linken Seite (gestrichelte Kurven) wurde um den Faktor 1,2 verkleinert. Dadurch sind die Kurven etwas weiter nach außen gewandert und der Umschlagpunkt, wo beide Lichtintensitäten in der Faser gleich sind, hat sich um etwa 3,5 m nach links verschoben. (FB) |
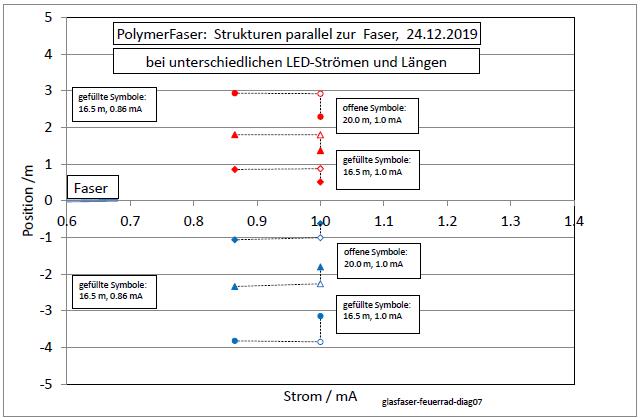 |
| Abb. 02-09: Probe aufs Exempel mit den simulierten Daten. Bei Beleuchtung mit nur einer Diode wurden die Strukturen ausgemessen für folgende Bedingungen: 1. Länge 20,0 m und 1,0 mADer aus der Abb. 02-08 abgeschätzte Faktor 1.2 bzw. dessen Kehrwert 0.8333 war nahezu richtig. Beim Probieren zeigte sich, daß beim Diodenstrom von 0.865 mA die Position bei 1. und 3. besser übereinstimmen (siehe horizontale gestrichelte Linien bei allen sechs Strukturelementen). (FB) |
 |
Abb. 02-10: Die drei unterschiedlichen Bedingungen bei Einspeisung vom oberen Bildrand1. 20 m, 1.0 mA, Blechmarken mit Draht zur Kamera(FB) |
Berechnung der materialspezifischen Dämpfung:
3,5 m Faserlänge weniger entspricht einer Stromänderung von 1.000 mA auf 0.865 mA d.h. Faktor 1.156
10 log (1.156) = 0.629
für 1 m gilt dann 0.629 / 3.5 = 0.180
Also ist die spezifische Dämpfung 0.180 dB/m bzw. 180 dB/km
Der Wert stimmt von der Größenordnung her mit den Herstellerangaben für 650 nm (LED): " <= 150 dB/km" überein.
www.fiber-shop.de/kunststoff-lwl/fertigkabel-pof-simplex.php
POF PE simplex
Dämpfung <=150 dB/km bei 650nm
Mantel PE schwarz, Maximale Zugkraft 120N
Durchmesser 2.2mm, Biegeradius 30mm
Temperaturbereich Betrieb:-20..+80°C. Verlegung:0..+50°C
Anwendungsbereich: Verlegung innerhalb Gebäuden
3. Fortgeschrittene Experimente, Fasern und Sonnenlicht
Ist es das Licht oder sind es Teilchen, die bei der Bremsstrahlung in der LED erzeugt wurden?
Annahme: Teilchen können durch eine mit Filzstift gefärbte Oberfläche der Glasfaser hindurchgehen.
 |
| Abb. 03-01: Meßkabel mit Bananensteckern, stellvertretend für die Faser: das eine Ende ist mit einem Filzstift permanent dunkel gefärbt, das andere nicht. (FB) |
 |
| Abb. 03-02: Noch unbehandeltes Faserende, das Licht vom anderen Ende scheint hindurch (FB) |
 |
| Abb. 03-03: Nun ist es mit Filzstift teilweise abgedunkelt. (FB) |
Fazit: Während bei unbehandelter Faser je nach Standort beide Richtungen des Lichtes zu verfolgen sind, ist bei der einseitig abgedunkelten Faser nur noch die eine Richtung spürbar. (" kommt mir entgegen / ich gehe mit....")
Also müssen die spürbaren Effekte mit etwas zusammenhängen, daß sich durch Farbe abschwächen läßt (Licht).
4. Experimente mit Bündeln aus Sonnenlicht.
 |
| Abb. 04-01: Zwei Spiegel reflektieren mit ihren planen Seiten das Sonnenlicht so, daß es jeweils auf den anderen Spiegel fällt. Abstand ca. 8 m (FB) |
 |
| Abb. 04-02: Etwas später ist die Sonne weitergewandert. Es gibt spürbare Strukturen, die von jedem Spiegel in Richtung zum Treffpunkt etwa in der Mitte zwischen beiden gehen. In der Nähe des Spiegels haben die Strukturen eine Richtung. Aus der Sicht des spürenden Beobachters: " ich gehe mit", "ich gehe entgegen". Ungefähr in der Mitte ändert sich der Eindruck. Dort ist keine Richtung spürbar. (FB) |
 |
| Abb. 04-03: Die beiden Schnüre markieren das spürbare Ende eines jeden Bündels. Dort weitet sich die Struktur auf. (FB) |
 |
| Abb. 04-04: Nimmt man die konvexen Seiten und stellt die Spiegel etwa im doppelten Abstand der Brennweite auf, dann sieht die spürbare Struktur ganz anders aus. Es gibt auf beiden Seiten der Symmetrieachse (Richtung der Sonnenstrahlen) jeweils zwei "Strahlen". Einer davon steht senkrecht zur Spiegeloberfläche. Man findet ihn sowohl vor als auch hinter dem Spiegel. (FB) |
 |
| Abb. 04-05: Ausschnitt, man sieht auf dem Glas das reflektierte Licht vom anderen Spiegel (FB) |
Literatur: b-literatur.htm
 |
www.biosensor-physik.de | (c) 27.12.2019 - 11.04.2020 F.Balck |
© BioSensor-Physik 2020
· Impressum
