Friedrich Balck > Biosensor > Physik > Indizierung

Beobachtungen:

Indizierung der Maxima in einem Beugungsmuster

Auftragung der Positionen gegen einen zugehörigen fortlaufenden Index


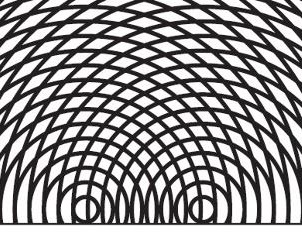
Abb. 01: Modell zur Überlagerung von zwei Wellenzentren, geometrische Konstruktion des Beugungsmuster. (Huygens-Prinzip) Von zwei Zentren gehen Kreise aus. Die Kreise des einen Systems schneiden die des anderen. Die Schnittpunkte liegen auf Linien, die mathematisch Hyperbeln darstellen. Zwischen zwei benachbarten Linien gibt es definitionsgemäß keine Schnittpunkte. An den oberen Rand des Bildes stoßen neun dieser Linien. Wegen der Symmetrie ist es sinnvoll, sie von der Mitte aus gesehen zu numerieren. Eine (logische) Zählweise, die auch bei Beugungsexperimenten in der Optik genutzt wird, wäre demnach: -4, -3, -2, -1, 0, 1, 2, 3, 4 In der Physikalischen Optik werden die Richtungen mit erhöhter Intensität in dieser Weise durchgezählt und als Beugungsordnung bezeichnet. siehe auch ueberlagerung (FB)	Abb. 02: Bei dieser Rechnung für einen Doppelspalt ist die Zählung nicht ganz so einfach. Offensichtlich gibt es eine Grob- und eine Feinstruktur. Sofern eine strenge Gruppierung vorliegt in der Form, daß pro Hauptmaximum immer eine feste Anzahl von Nebenmaxima auftreten, dann wäre eine Indizierung mit einer fortlaufenden Nummer für die Hauptmaxima und ein rationaler Bruch für die Nebenmaxima (als Dezimalzahl) sinnvoll. Beispielsweise bei 5 Nebenmaxima pro Gruppe: -2, -1.8 , -1.6 , -1.4 , -1.2 , -1.0, usw. Gleiche Überlegungen könnten auch gelten, wenn bei einem einfach zählbaren Beugungsmuster sich ein weiteres überlagert, das von einer zweiten Wellenlänge in der Strahlung verursacht wird. Beispiel Mensa ?? (FB)

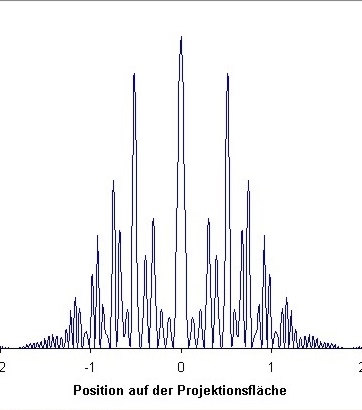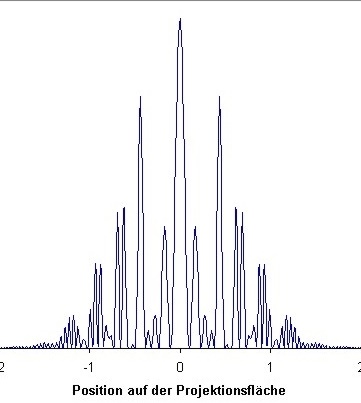
Abb. 03: Beugungsmuster eines Doppelspaltes gerechnet für kurzen Abstand zur Projektionsfläche. (FB)	Abb. 04: Beugungsmuster eines Doppelspaltes gerechnet für kurzen Abstand zur Projektionsfläche. Die Muster beider Rechnungen unterscheiden sich, weil ein Parameter für die Rechnung geändert wurde (Abstand der Spalte 0,5 bzw. 0,6). Doppelspalt-Rechnung Offensichtlich ist es schwierig, eine einheitliches Schema für die Bezeichnung der Maxima anzugeben. In der unmittelbaren Nähe des mittleren Maxiums ändern sich die Intensitäten sehr stark, daher ist eine einheitliche Zuordnung nicht möglich. Weitere Rechnungen mit feinerer Abstufung des Parameters könnten hier für etwas mehr Klarheit sorgen. (FB)

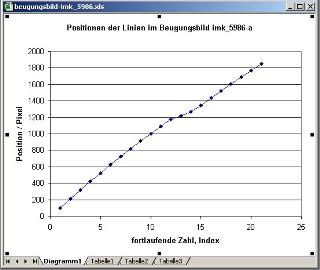
Abb. 05: Beugungsbild eines zum Strich aufgeweiteten Laserstrahls. Die Zählung beginnt links mit der Nummer 1. Das hellste Maximum hat demnach die Nummer 12. (FB)	Abb. 06: s-förmige Kurve: Position der Maxima gegen eine fortlaufende Zahl (Index) Beim Index 12 ist die Position des hellsten Maximums. gitterbeugung (FB)

Abb. 07: Bestimmung der Position einzelner Störungslinien und deren Auftragung gegen einen fortlaufenden Index. Wenn die Abstände im Mittenbereich etwas geringer als im Außenbereich sind, ergibt sich eine gespiegelte s-förmige Kurve. (FB)