Friedrich Balck > Biosensor > Versuche > Torkelnde Felder

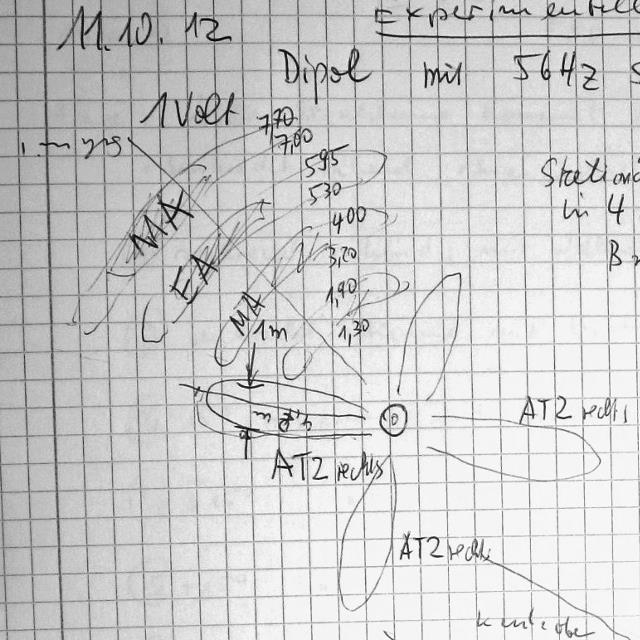
Beobachtungen:

"Torkelnde Felder", Spinning Fields, Torsion Fields

Noch in Arbeit!!

Torsionsfelder, Torsion Fields

Y.V.Nachalov, E.A.Parkhomov
        Experimental detection of the torsion field. http://amasci.com/freenrg/tors/doc15.html, gefunden am 4.2.2014

Protokoll der Experimente

In der klassischen Elektrodynamik kennt man Hertzsche Wellen. Sie gehen von einem ruhenden Dipol aus.
Der Vektor der elektrischen Feldstärke dieser Wellen steht parallel zum Dipol und hat daher konstant die gleiche Richtung.
Was passiert, wenn der Dipol nicht feststeht, sondern oszillierende Bewegungen ausführt?
Vermutung: der Vektor der Feldstärke oszilliert auch, d.h. er taumelt. Die Wellen laufen auf "Schlangenlinien".
Ein ruhender Beobachter in größerem Abstand zum Dipol wird eine elektromagnetische Welle empfangen, die nicht 100% linear polarisiert ist. Je nach Form der Dipolbewegung können beim Beobachter unterschiedliche Schwingungsformen auftreten.
Eine einfache Version ist die zirkulare elektromagnetische Welle. Sie tritt auf, wenn der Dipol um eine zu ihm senkrechte Achse rotiert und diese Achse zum Beobachter zeigt.
Es gibt aber noch weitere Schwingungsformen.

Beobachtung: Offensichtlich können biologische Sensoren bei langsamen Oszillationen unterschiedliche Schwingungsformen wahrnehmen und unterscheiden.
War das in unserer Entwicklungsgeschichte eine wichtige Voraussetzung für das Überleben?
Beute und Angreifer machen sich durch torkelnde elektromagnetische Wellen bemerkbar.

Torsionsfelder lassen sich mit zwei Geräten meßtechnisch erfassen.
IndikatorGeophysikalischeAnomalien IGA-1 von Juri Kravchenko, Russland
    http://www.iga1.ru/iga.html
SpinningElectricVectorAnalyser SEVA von Mark Krinker, USA
    http://www.royriggs.co.uk/www.royriggs.co.uk/Geopathic_Water.html
    http://de.scribd.com/doc/72708396/Photonic-Aspects-of-Dowsing-and-Feng-Shui

Beide Geräte messen die Phase von elektromagnetischen Wellen.
Unterschiede der Geräte sind im Patent von M. Krinker in Abschnitt 0011 bis 0016 aufgelistet: /Krinker 2007/
Das SEVA bestimmt die Phasendifferenz zwischen zwei orthogonalen elektromagnetischen Wellen gleicher Frequenz.

Offensichtlich ändert sich bei zirkularen elektromagnetischen Wellen im Niederfrequenzbereich das Verhältnis von Ausbreitungs- und Rotationsgeschwindigkeit bzw. die Drehrichtung, wenn sie mit Hindernissen oder Grenzflächen wechselwirken.
Somit sind Phasenänderungen der Wellen ein Hinweis auf die Existenz und Eigenschaften von Hindernissen oder Grenzflächen.

In der Optik kennt man, daß zirkularpolarisiertes Licht bei schrägem Einfall auf eine Glasscheibe seine Polarisationseigenschaft ändert. Man nutzt diese Eigenschaftsänderungen zur Materialanalyse. Stichwort: Ellipsometrie

weitere Effekte und Experimente zu torkelnden Feldern   torkelnde-felder-zwei.htm

Bei Licht gibt es komplexe Schwingungsformen des elektrischen Vektors.
z.B.
/Secor 2017/ Complex Light

"On the other hand, one particular form of complex light is that of radial polarization, which is a condition where the electric-field vector everywhere points outward (this would be homogenous in cylindrical co-ordinates and we’ll come back to the ideas of co-ordinate systems in the next section). The electric-field vector in this case is not the same along a path that circles the beam profile (in contrast to the linearly polarized case). The horizontal and vertical directions give a simple basis set for homogenous light polarization, while new forms of radial and azimuthal polarization form an orthogonal set that can be used to describe light.

Another popular group of complex light beams are those that carry orbital angular momentum. Classical and quantum physics deals with orbital angular momentum in a variety of situations, but its treatment within the realm of lightbeam propagation is central to advances in the understanding and application of complex light. In 1936, Richard Beth demonstrated that circularly polarized light could transfer spin angular momentum to matter, thereby causing it to rotate [1]. Seventy years later, the same effect was observed with the orbital angular momentum of light.
Beth R A 1936 Mechanical detection and measurement of the angular momentum of light, Phys. Rev. Lett. 50 115"

/Padgett 2014/ Light's Twist

"(orbital angular momentum, OAM)
For OAM, the mathematically analogous states to circular and linear polarization are the helically phased Laguerre–Gaussian laser modes and the Hermite–Gaussian modes, respectively. A birefringent waveplate has no effect on the mode, and hence OAM, of the transmitted light, but a modal transformation can be introduced by clever use of cylindrical lenses [7] or the inversion properties of a Dove prism.
[7] Beijersbergen MW, Allen L, van der Veen HELO, Woerdman JP. 1993 Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 96, 123–132. (doi:10.1016/0030-4018(93)90535-D)"

https://en.wikipedia.org/wiki/Angular_momentum_of_light

https://en.wikipedia.org/wiki/Orbital_angular_momentum_of_light

Abb. 00-00: Orbital angular momentum,
https://upload.wikimedia.org/wikipedia/commons/3/35/Helix_oam.png

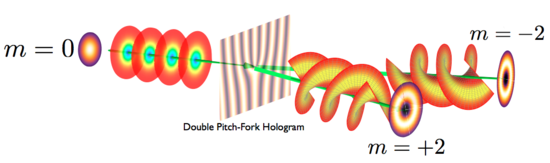Abb. 00-00a:
"A more convenient approach for generating OAM is based on using diffraction on a fork-like or pitchfork hologram (see figure). Holograms can be also generated dynamically under the control of a computer by using a spatial light modulator."
Erzeugung z.B. durch eine steuerbare (durchlässige) Schicht mit Flüssigkristallen.
https://en.wikipedia.org/wiki/File:Hologram_generation.png

/Wilson 2010/ Holograms tie optical vortices in knots

Erzeugung von Lichtwirbeln durch Hologramme

Inhalt

0. Hertzsche Wellen bei bewegter Quelle, zirkulare Wellen
1. SEVA über Geopatischen Zonen
2. Rotierender Dipol im Labor, SEVA
3. Rotierender Dipol im Freien, spürbare Zonen
4. Stromführendes Kabel

0. Hertzsche Wellen bei bewegter Quelle, Zirkulare Wellen

Es gibt elektromagnetische Wellen möglicherweise unterschiedlicher Art:

0. stehender Dipol (Klassische EM-Wellen)
1. Lineare Bewegung des Dipols
2. Lineare oszillierende Bewegung des Dipols, die Richtung des Dipols im Raum bleibt konstant
2.1 in Richtung des Beobachters (longitudinal)
2.2 quer zum Beobachter, quer zur Dipolachse
2.3 quer zum Beobachter, in Richtung der Dipolachse

3. oszillierende Bewegung des Dipols, der Mittelpunkt des Dipols bleibt auf der Achse zum Beobachter ortsfest
3.1 der Dipol führt eine Drehschwingung aus um die Achse zum Beobachter
3.2 der Dipol führt eine Drehschwingung aus, wobei die Spitzen des Dipols abwechselnd zum Beobachter zeigen.

4. rotierende Bewegung des Dipols um die Achse zum Beobachter, der Mittelpunkt des Dipols bleibt ortsfest.

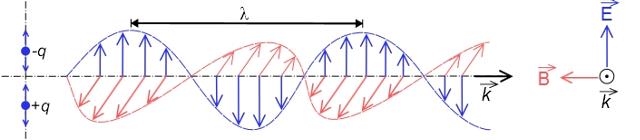Abb. 00-01: Elektromagnetische Welle, rot: magnetisches Felde, blau: elektrisches Feld
http://upload.wikimedia.org/wikipedia/commons/3/35/Onde_electromagnetique.svg

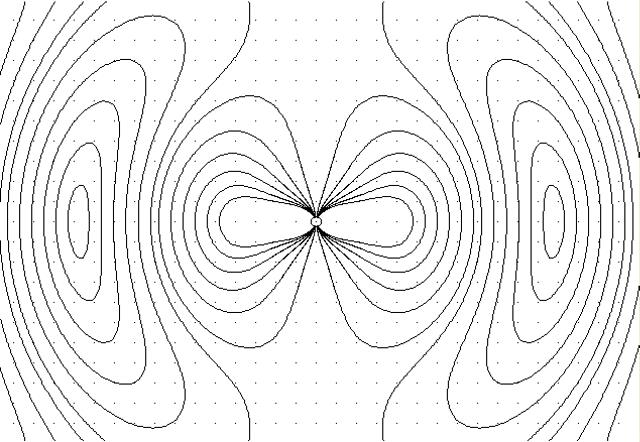Abb. 00-02: Strahlung eines Dipols, elektrische Feldlinien
der Dipol ist der kleine Kreis in der Mitte mit Polung + oben, - unten bzw. zu einem späteren Zeitpunkt umgekehrt. Gerechnet auf der Seite von http://www.schulphysik.de/dipol.html

Abb. 00-03:
Vorne: Quadrupolkondensator, wirkt als Sender und als Empfänger für zirkulare Wellen.
    physik-neu-005.htm
Mitte:   IGA-1 IndikatorGeophysikalischeAnomalien IGA-1 von Juri Kravchenko, Russland
    http://www.iga1.ru/iga.html
hinten: SEVA SpinningElectricVectorAnalyser SEVA von Mark Krinker, USA
    http://www.royriggs.co.uk/www.royriggs.co.uk/Geopathic_Water.html
(FB)

1. SEVA über Geopatischen Zonen (GPZ)

Es lassen sich mit SEVA periodische Signale über geopatischen Zonen messen.

Mark Krinker, USA (SEVA) antwortet auf die hier vorgestellten Beobachtungen dieser Signale:

"I encounter this phenomena in USA.
Looks like it matches to what my Russian colleagues call a "kryak" - the sound a duck made. (when connect to a sound card, the frequency of repetition about 1Hz)
They discovered it in a lot of GPZs and we still have no final explanation.
We now that lines of GPZs are wave guides and this is related to that."

Er hat dieses Phänomen in den USA beobachtet. Es scheint sich mit den Effekten zu decken, die meine russischen Kollegen "KRYAK" nennen, etwa so wie das Geschrei von Enten.
(Wenn man das Signal an eine Soundkarte anschließt, findet man eine Wiederholrate von ungefähr ein Hertz.)
Sie entdeckten es bei vielen GPZs und wir haben aber noch keine Erklärung dafür.
Wir wissen, daß die Zonen wie Wellenleiter wirken und daß das damit zusammenhängen könnte.

wellenleiter

Abb. 01-01: Kabeltrommel ohne Last aber am Netz, SEVA in der Nähe eine Kabelschlaufe.
Signal pulsiert etwa mit 1 Hz. (FB)

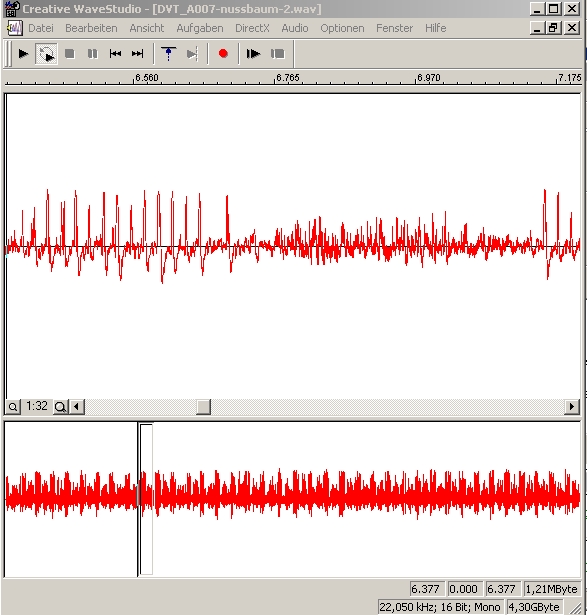Abb. 01-02: Aufzeichnung des Signals, oben mit höherer Zeitauflösung dargestellt.
Der Ausschnitt oben etwa von 6,377s bis 7,18s entspricht dem Zeitfenster bei der unteren Kurve. (FB)

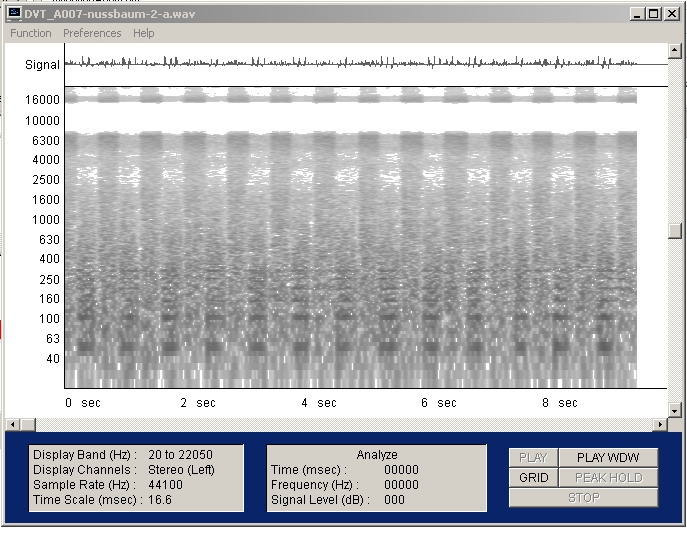Abb. 01-03: Frequenzananlyse, niedrige/hohe Amplitude entspricht hell/dunkel.
Auffallend sind die Vielfachen (Harmonischen) der Netzfrequenz von 50 Hz. (FB)

Abb. 01-04: Wiederholung mit besserem Aufbau (FB)

Abb. 01-05: Die Kabelschlaufe befindet sich über zwei geopathischen Zonen (GPZ)
Doppeltes Hartmanngitter und einfaches Currygitter (FB)

Abb. 01-06: Aufzeichnung des Signals mit Diktiergerät
MP3-Format, möglicherweise gibt es Artefakte bei der Frequenzanalyse durch das Aufzeichnungsverfahen. (FB)

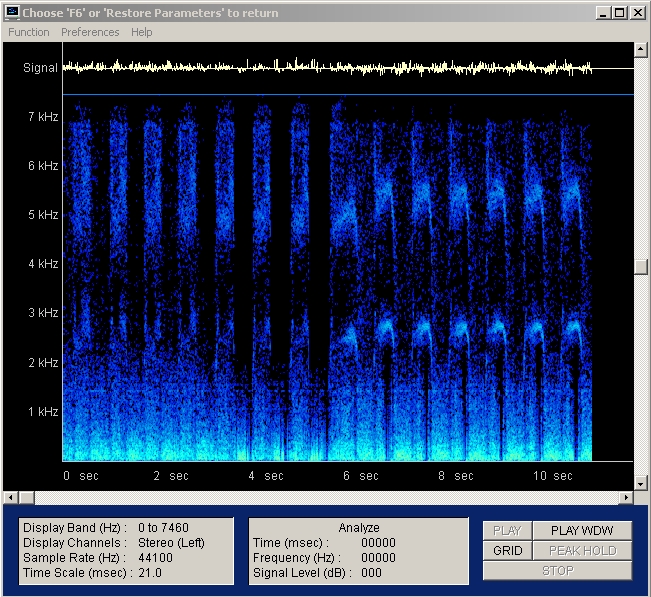Abb. 01-07: Frequenzanalyse, lineare Frequenzachse bis 7 kHz (FB)

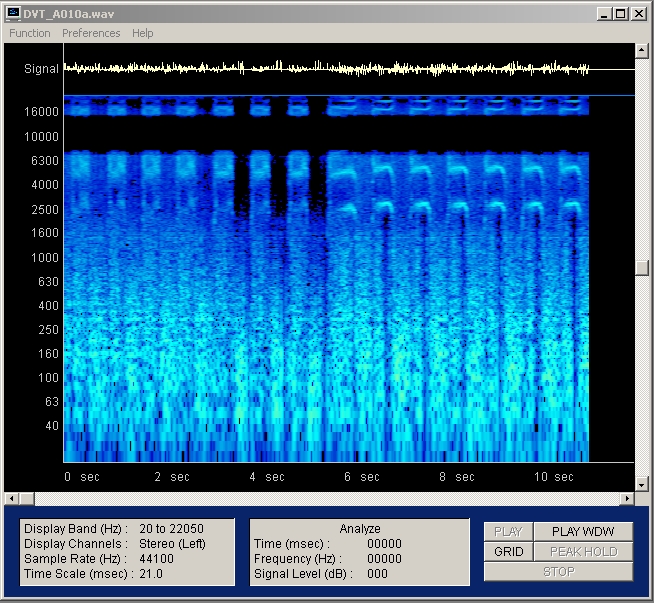Abb. 01-08: Frequenzanalyse, logarithmische Frequenzachse bis 7 kHz (FB)

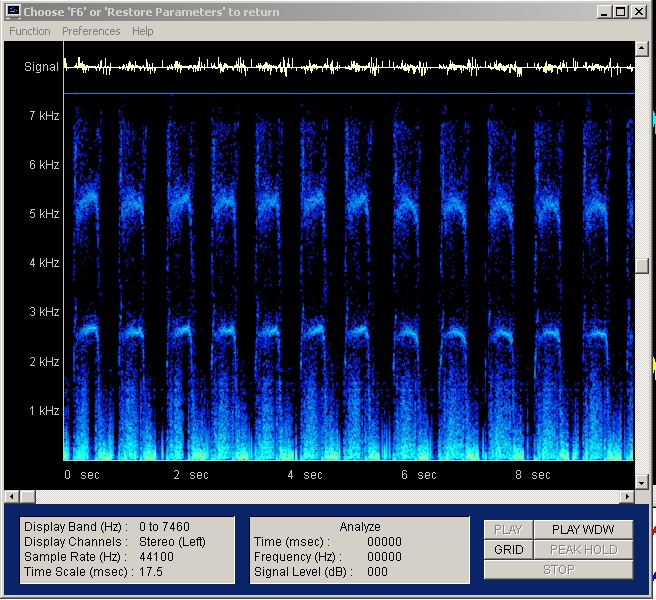Abb. 01-09: Frequenzanalyse, lineare Frequenzachse bis 7 kHz, Zeitachse gedehnt. (FB)

Abb. 01-10: Frequenzanalyse, lineare Frequenzachse bis 7 kHz, Zeitachse gedehnt. (FB)

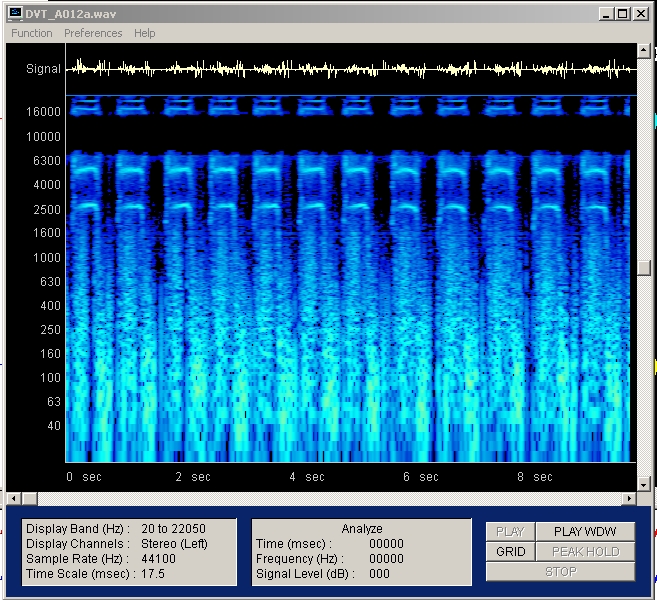Abb. 01-11: Frequenzanalyse, logarithmische Frequenzachse bis 7 kHz (FB)

2. Rotierender Dipol im Labor, SEVA

Umdrehung etwa mit 1 Hz, Spannung 1Volt ss

Abb. 02-01: Dipol auf Drehteller, rotiert mit etwa 1 Umdrehung pro Sekunde.
Die Signale des SEVA werden mit einem Musikrekorder aufgezeichnet. (FB)

Abb. 02-02: Dipol und SEVA aus der Nähe (FB)

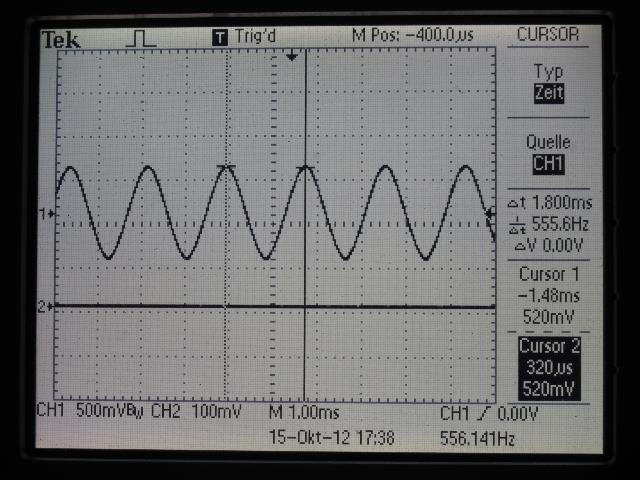Abb. 02-03: Anregung des Dipols mit Sinusspannung, 556 Hz, 1 Volt ss (FB)

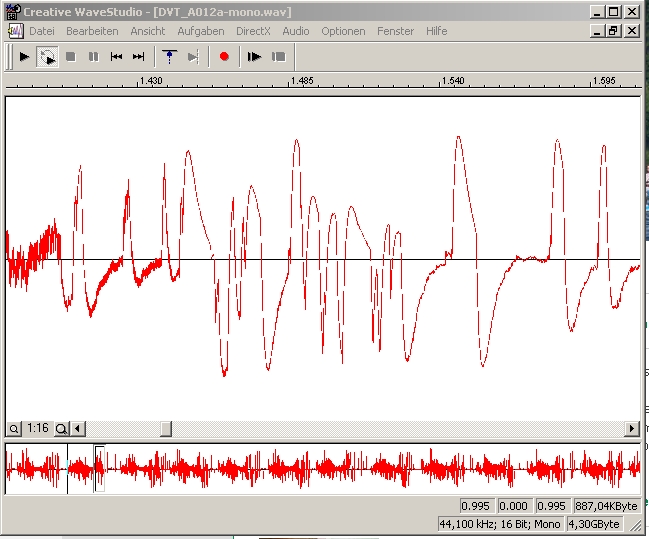Abb. 02-04:Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 1.4 bis 1.6 s (FB)

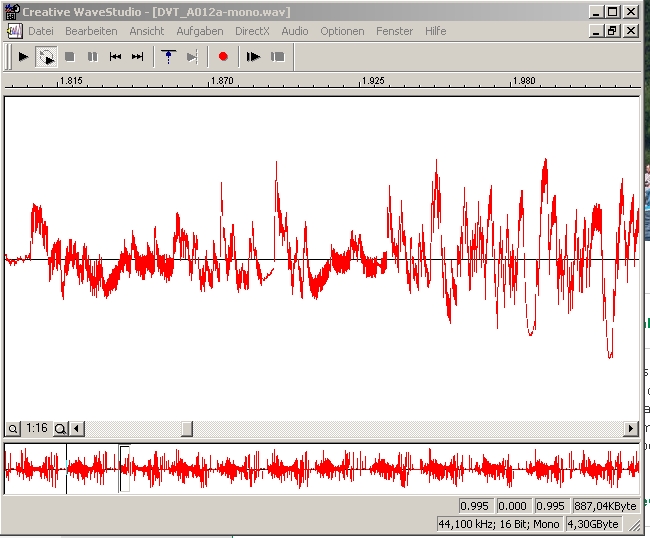Abb. 02-05 Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 1.8 bis 12,0 s (FB)

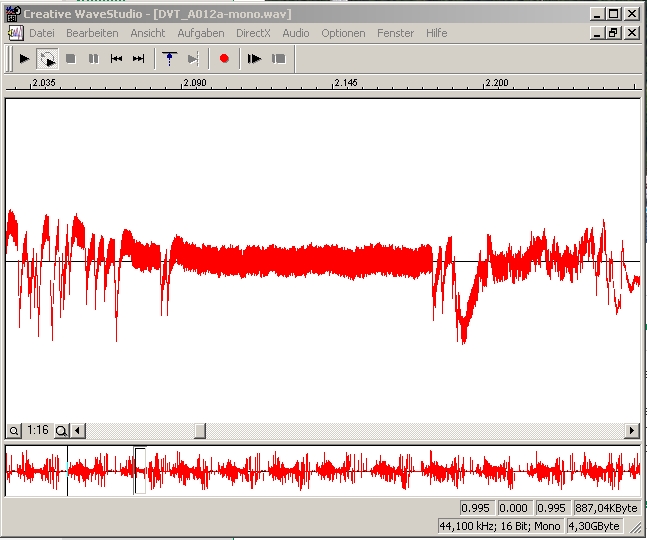Abb. 02-06: Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 2,0 bis 2,25 s (FB)

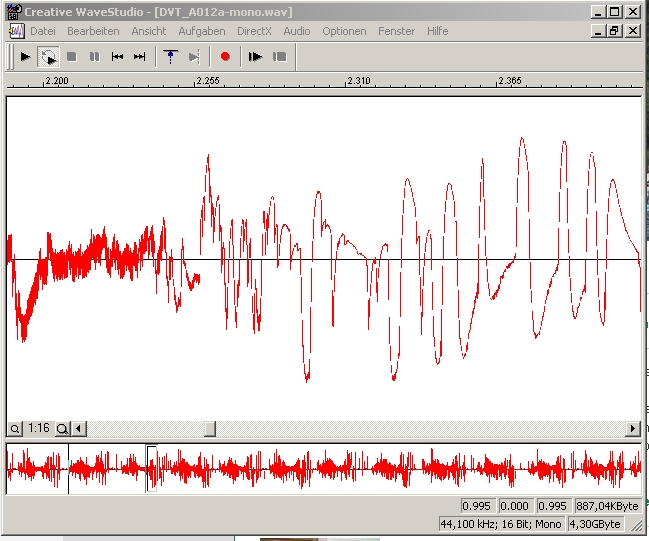Abb. 02-07: Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 2,2 bis 2,5 s (FB)

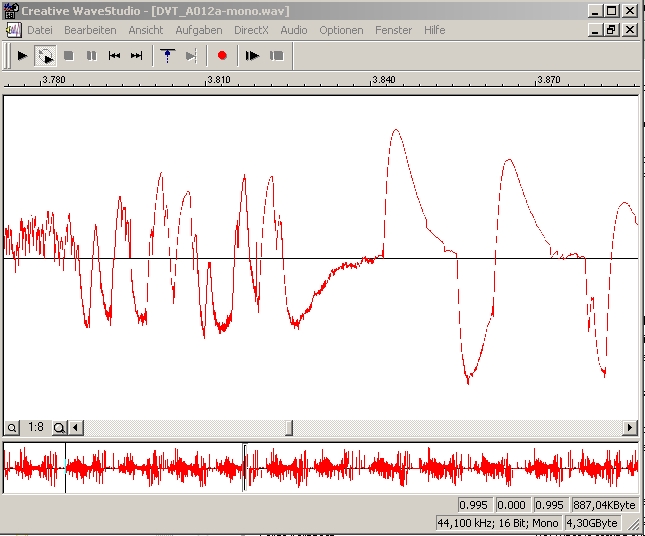Abb. 02-08: Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 3,7 bis 3,9 s (FB)

Abb. 02-09: Mit rotierendem Dipol. Das Signal, analog aufgezeichnet. Zeitfenster 5,3 bis 5,5 s (FB)

Abb. 02-10: Mit rotierendem Dipol. Frequenzanalyse, lineare Frequenzachse.
Deutlich als "Leitern" mit gleichen Abständen sind die Harmonischen der Anregefrequenz von 556 Hz zu sehen. Auf der Zeitachse dazwischen, etwa alle Sekunde, gibt es Streifen mit höherer Intensität.
Die Amplitude ist als Helligkeit kodiert, je größer um so heller ist die Darstellung.
(FB)

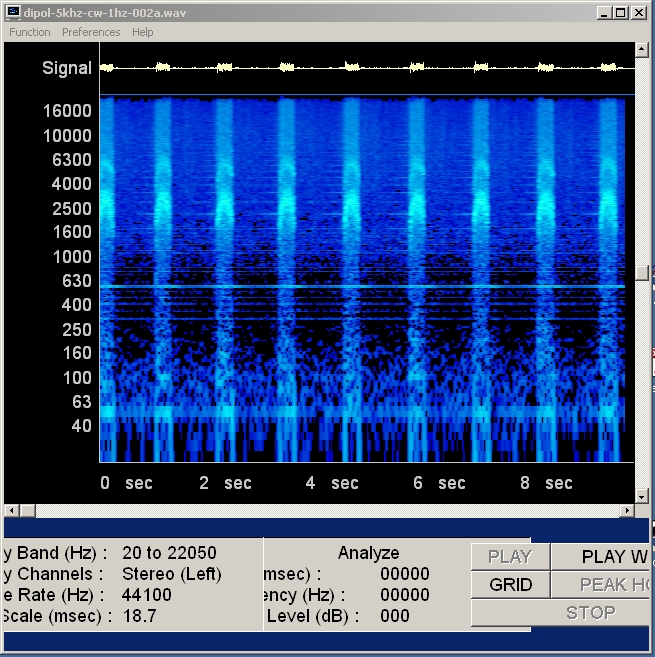Abb. 02-11:Mit rotierendem Dipol, logarithmische Darstellung (FB)

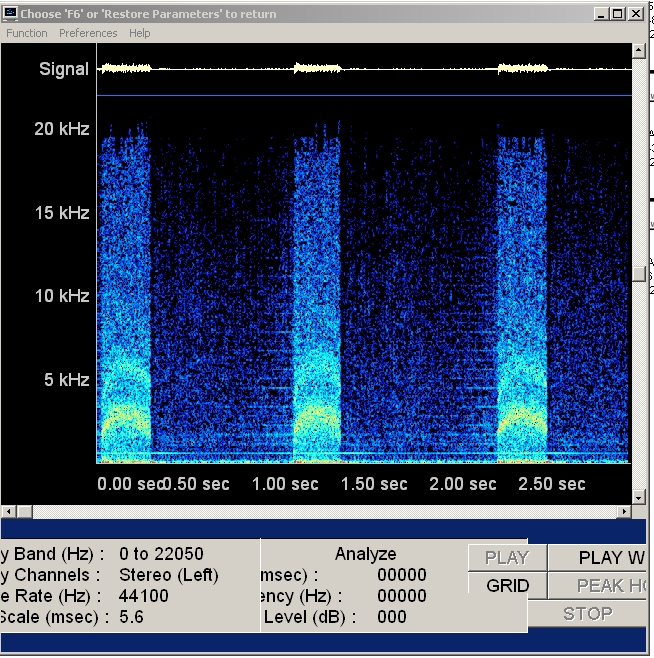Abb. 02-12: Mit rotierendem Dipol. Ausschnitt, lineare Achse (FB)

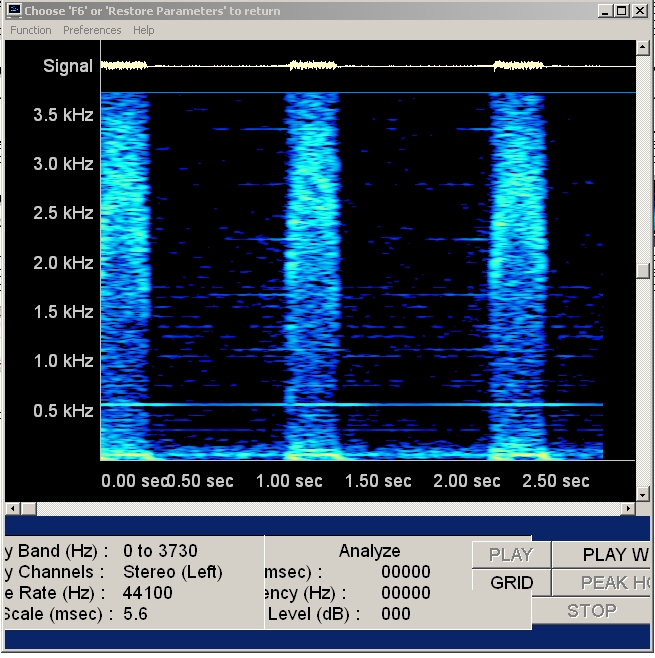Abb. 02-13:Mit rotierendem Dipol. Ausschnitt, Frequenz bis 3,5 kHz (FB)

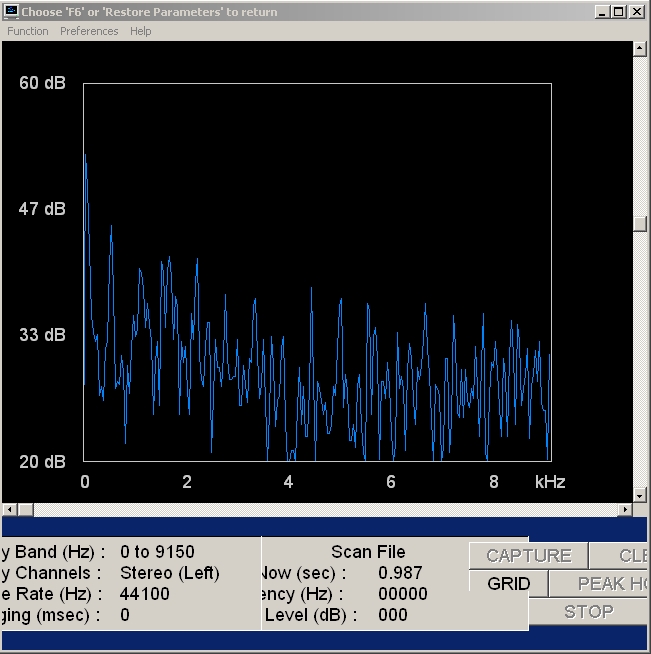Abb. 02-14: Mit rotierendem Dipol. Frequenzanalyse, Amplitude gegen Frequenz. Zeit 0.987 s

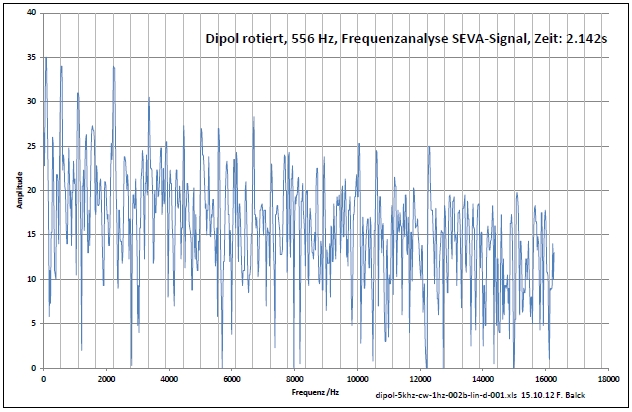Abb. 02-15: Mit rotierendem Dipol. Frequenzanalyse zur Zeit 2.142s. Das Raster hat einen Abstand von 556 Hz. Dadurch sind die Harmonischen der Dipolfrequenz gut zu erkennen. (FB)

3. Rotierender Dipol im Freien, spürbare Zonen

Abb. 03-01: Der Dipol rotiert mit einem Drehteller. Seine Achse läßt sich neigen.
Frequenzgenerator mit Batterie drehen sich mit. (FB)

Abb. 03-02: Dipolachse parallel zur Drehachse.
Ohne Wechselspannung und Stillstand gibt es keine spürbaren Strukturen. (FB)

Abb. 03-03: Dipolachse um etwa 15 Grad zur Drehachse geneigt. Generator in Betrieb. Teller rotiert mit etwa ein Umdrehung pro Sekunde. Der Vektor der elektromagnetischen Welle "torkelt". (FB)

Abb. 03-04: Die spürbaren Zonen sind ausgelegt.
Einstellung: Generator 56 Hz, Dipol senkrecht, keine Rotation (FB)

Abb. 03-05: Die spürbaren Zonen sind ausgelegt. Es gibt vier kissenförmige Bereiche in Blickrichtung der Kamera und vier keulenartige Strukturen (wie Windmühlenflügel).
Einstellung: Generator 56 Hz, Dipol senkrecht, keine Rotation. (FB)

Abb. 03-06: Der Dipol rotiert in Bildmitte. Durch die Rotation vergrößert sich die Reichweite der spürbaren Strukturen bis über 30 Meter.
Einstellung: Generator 56 Hz, Dipol etwa 15 Grad geneigt, Rotation 1 Hz.(FB)

Abb. 03-07:
1) Strukturen bei stillstehendem Dipol, 56 Hz, 1 Volt ss,
Angaben der Maße in Meter.
Die gezeichneten Strukturen gibt es doppelt, jeweils oberhalb und unterhalb der Ebene durch die Drehachse. Sie wandern nach Neigen des Dipols mit. Bei den Keulen gibt es oberhalb die Qualität AT2 rechts und unterhalb AT1. Die Kissen haben zwei Qualitäten EA und MA

2) Strukturen bei Rotation mit 1 Hz, 56 Hz, 1Volt ss
Bei Rotation verschwinden die keulenförmigen Strukturen. Die kissenförmigen sind konzentrisch, haben zwei unterschiedliche Qualitäten und reichen sehr weit nach außen.
FB spürt bei den ringförmigen Zonen im Außenraum (10 Meter) unterschiedliche Qualitäten, je nachdem er sich auf die Drehachse zu oder von ihr weg bewegt. (FB)

4. Stromführendes Kabel

Das Kabel besteht aus drei Adern: Phase, Null und Schutzleiter.
Zwischen Phase und den beiden anderen liegt die Wechselspannung von 230 Volt.
Diese Drähte wirken wie eine langgestreckter Kondensator.
Bei der Fertigung des Kabels hat man das Bündel der drei Adern spiralförmig verdrillt. Daher fließt der Strom auf kleinen Spiralbahnen.

Bei gestrecktem Kabel lassen sich vier konzentrische Zonen spüren.
Biegt man das Kabel jedoch zu einer Bogen, dann sind weitere Strukturen zu beobachten. Der Strom fließt in der Biegung ähnlich wie in einer Toroidspule. physik-neu.htm

Mit Hilfe vom IGA-1 Detektor lassen sie die Effekte der Schlaufe quantitativ messen.
Das Gerät gibt deren Größe in einer Digitalanzeige an:
zwei Versuche: 1. bei Annäherung an die Schlaufe, 2. beim Darübergehen.
Bei geradlinig verlegtem Kabel zeigt das Gerät keine Änderungen an.

---------------
Die Empfehlung, in Schlafbereichen die stromführenden Leitungen nachts abzuschalten, macht offensichtlich Sinn.
Dies ist besonders dann zu empfehlen, wenn die Kabel aufgerollt oder mit Schlaufen verlegt sind.

Abb. 04-01: Dreiadriges Kabel 3 x 0,75, flexibel, die Verdrillung der einzelnen Adern hat eine Periode von rund 9 cm. (FB)

Abb. 04-02: In dieser Schlaufe des Kabels läuft die blaue Ader zweimal um die beiden anderen herum. (FB)

Abb: 04-03: Spannungsführendes Kabel, dreiadrig, 230 Volt Wechselstrom.
Um das Kabel herum findet man konzentrisch vier spürbare Zonen.
Die Radien sind 6 cm -13 cm; 24 cm - 33 cm; 050 cm - 58 cm; 78 cm - 87 cm.
In Längsrichtung sind die Zonen abschnittsweise (Länge 1,2 m) eingeschnürt.
(FB)

Abb. 04-04: Spannungsführendes Kabel mit Schlaufe.
Aus der Schlaufe heraus kommen große spürbare Zonen, etwa 1/2 Meter groß, neben und über der Schlaufe unterscheiden sie sich in ihrer Form (seitlich sind sie ballonförmig).

Abb. 04-05: Oberhalb der Kabelschlaufe wird das IGA-1 eingesetzt, um Torsionsfelder zu messen.
Während der Messung wird der RESET-Knopf gedrückt gehalten, so daß das Digitalmultimeter die Kompensationsspannung anzeigt. Diese ist ein Abbild der Meßgröße.
Spannung 7,25 Volt. (FB)