Friedrich Balck > Biosensor > Physik > gekoppelt

Beobachtungen:

gekoppelte Schwingungen, Energieaustausch

Resonanz

Zwei oder mehrere gleichartige schwingungsfähige Systeme können untereinander Energie austauschen, wenn sie leicht miteinander gekoppelt sind. Beispielsweise kann ein schwingendes Pendel ein zunächst ruhendes zum Schwingen anregen.

Hierbei überträgt sich die Energie über die Kopplung wechselweise von dem einen zum anderen System. Dieser Prozeß kann sich solange wiederholen, bis die Gesamtenergie aufgebraucht worden ist.

Der Energieübertrag arbeitet dann besonders gut, wenn beide Schwinger die gleiche Resonanzfrequenz haben. Resonanz

Verbindet man zwei gleichartige schwingende Systeme (mit gleicher Resonanzfrequenz) "lose" miteinander, so daß jedes für sich alleine schwingen kann, aber dennoch etwas von der Schwingung des anderen "erfährt", dann gibt es gekoppelte Schwingungen. Beide Systeme schwingen dann in Resonanz. resonanz
Erstaunlicherweise gibt es beim Koppeln von zwei Systemen leichte Änderungen in der gemeinsamen Resonanzfrequenz, denn es treten dabei zwei Frequenzen für die Resonanz auf.
Wenn sie "gegeneinander" schwingen, erhöht sich die Frequenz, bei "miteinander" erniedrigt sie sich etwas.

Vergrößert man die Anzahl derartig gekoppelter Schwinger, so gibt es mit jedem zusätzlichen Schwinger eine weitere Eigenfrequenz, die zu unterschiedlichen Schwingungsmoden gehört:

Typ								Beispiel Frequenz
Mode1	-->	-->	-->	-->	-->	alle gleichsinnig	niedrige Frequenz	208 Hz
Mode2	-->	-->	0	<--	<--			405 Hz
Mode3	-->	0	<--	0	-->			578 Hz
Mode4	-->	<--	0	-->	<--			702 Hz
Mode5	-->	<--	-->	<--	-->	alle gegeneinander	hohe Frequenz	793 Hz

In der Festkörperphysik nutzt man zur Beschreibung der mechanischen Eigenschaften eines Festkörpers ein Modell von mit Federn gekoppelten Atomen. Durch die hohe Zahl der bei einer mechanischen Schwingung beteiligten Atome gibt es sehr viele Frequenzen oder auch Frequenzbereiche, mit denen sich Schwingungen ausbreiten können. (Bänder)

Abb. 01: Zwei über eine Feder gekoppelte Fendel. Der dünne Aufhängedraht bildet hierbei die Koppelfeder.
Wenn zunächst ein Pendel schwingt, sorgt es für leichte Bewegungen der Aufhängung und regt somit das zweite Pendel an. Wenn die Resonanzfrequenzen beider Pendel übereinstimmen, kann es hierbei zu einem ständigen Energieaustausch zwischen beiden Systemen kommen.
Betrachtet man diesen Aufbau von der anderen Seite, dann ist das eine Pendel unsichtbar hinter der schwarzen Wand versteckt. Es sieht dann so aus, als ob das sichtbare Pendel aus unerklärlichen Gründen stehen bleibt und plötzlich wieder mit dem Schwingen beginnt.

Regt man beide Pendel gleichzeitig an, so daß sie gleiche Energie haben, findet kein Austausch statt.

Startet man die Pendel gleichsinnig, dann biegen beide den Aufhängebügel in die gleiche Richtung, so daß dieser für jedes Pendel etwas weicher zu federn scheint. Die Pendelfrequenz ist daher geringfügig niedriger als die eines einzelnen Pendels.
Startet man sie gegensinnig, tritt der umgekehrte Effekt ein. Der Bügel erscheint härter. Die Pendelfrequenz ist geringfügig größer.

(FB)

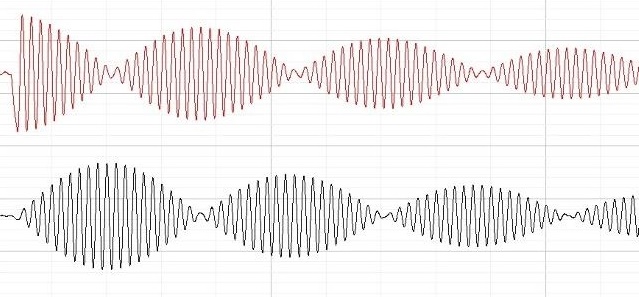Abb. 02: Verlauf der Schwingungen von zwei gekoppelten Pendeln. Die Energie wechselt periodisch von dem einen zum anderen und zurück. Wegen der Reibung nehmen die Maximalausschläge langsam ab.
Nach jeder Ruhepause nimmt die Amplitude zunächst linear zu. (FB)

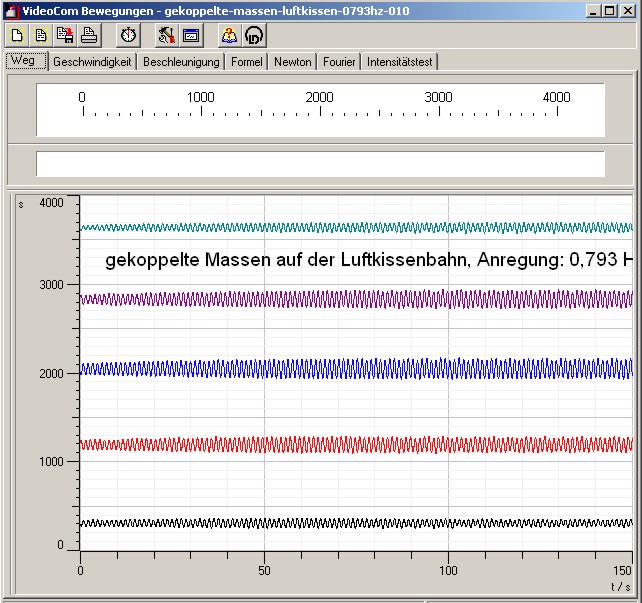
Abb. 03: Auf einer Luftkissenbahn gleiten fünf Massen, die mit schwachen Federn miteinander verbunden sind. Diese Federn-Massen-Kette ist am rechten Ende festgesetzt, am linken Ende wird sie mechanisch mit einstellbarer Frequenz angetrieben.
Auf jeder Masse klebt links ein weißer Reflektorstreifen. Damit kann eine Videokamera die Position der Masse bestimmen und deren zeitlichen Verlauf aufzeichnen. (FB)

Abb. 04: Fünf Massen und sechs Federn bestimmen die Eigenschaften dieses gekoppelten Systems.
(FB)

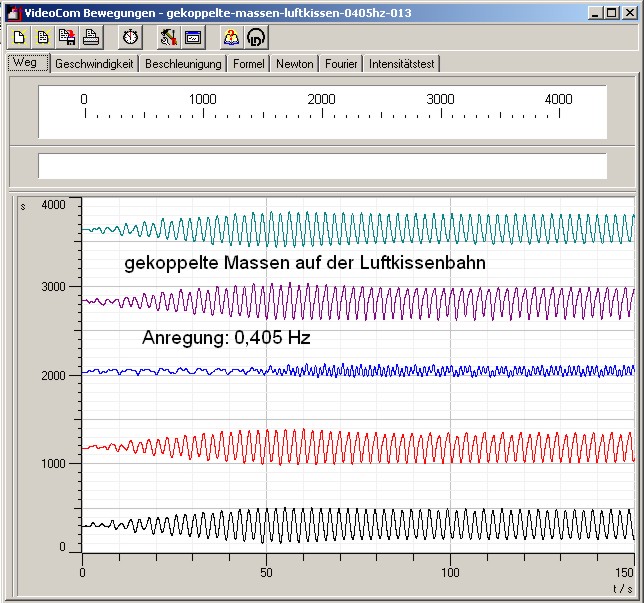
Abb. 05: Schwingung Typ 1: Wenn alle Massen gleichsinnig schwingen, dann ändert sich deren Abstand untereinander nicht. Die Schwingungsfrequenz ergibt sich allein aus den beiden Federn an den Enden der Kette und ist daher niedrig. (FB)

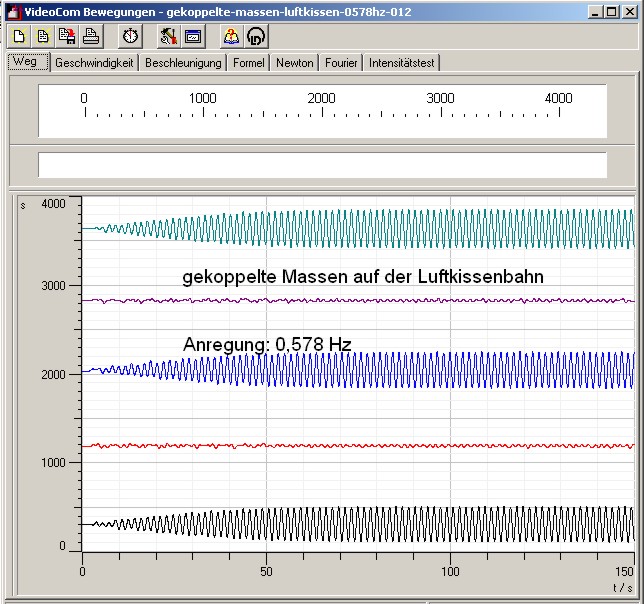
Abb. 06: Schwingung Typ 2: Jeweils die äußeren beiden Schwinger bewegen sich gleichsinnig. Der mittlere ruht. Die linken Massen bewegen sich entgegengesetzt zu den rechten.
Vier Federn werden beansprucht. (FB)

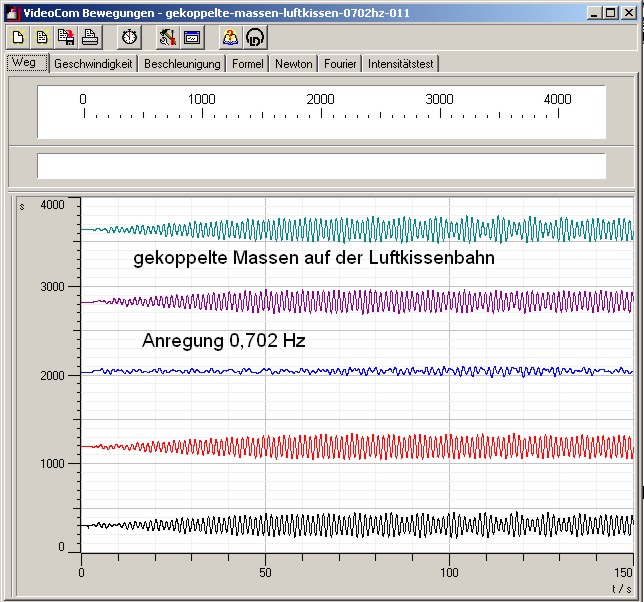
Abb. 07: Schwingungs Typ 3: Jeweils die ungeraden Schwinger bewegen sich gegeneinander, die geraden ruhen (FB)

Abb. 08: Schwingungstyp 4: die mittlere Masse ruht, jeweils die äußeren bewegen sich gegeneinander (FB)

Abb. 09: Schwingungstyp 5: alle unmittelbar benachbarten Massen schwingen gegeneinander. Alle Federn werden beansprucht, daher ist die Frequenz hoch. (FB)

Abb. 10: Frequenzanalyse der möglichen Schwingungen dieser Kette.
Regt man das ruhende System mit einem einzigen Impuls an, dann treten Schwingungen auf, bei denen automatisch alle möglichen Frequenzen zu finden sind, allerdings mit unterschiedlichen Amplituden.

Abb. 11: Eine besondere Kopplung von zwei unterschiedlichen mechanischen Schwingungen:
Rotationsbewegung um die Längsachse und Linearbewegung auf und ab.
Bei richtiger Abstimmung wechseln Rotations- und Linearbewegung einander ab. Mal steckt die Energie in der einen, mal in der anderen Bewegungsform. Wilberforce-Pendel (Wilberforce 1861-1944)

Der periodische Energieaustausch findet bei allen gekoppelten Pendeln (selbstverständlich) aber nur dann statt, wenn die beteiligten Schwingungssysteme unterschiedliche Startenergien haben.
(FB)

Musikinstrumente, gekoppelte Schwingungen

Monochord mit vielen Saiten

Zwanzig Saiten sind auf die gleiche Frequenz gestimmt. Der Resonanzkasten als gemeinsame Träger koppelt die Saiten mechanisch miteinander. Wenn die Saiten alle exakt eingestellt sind, wird man bei optimaler Kopplung theoretisch auch zwanzig Frequenzen erwarten.

Das Problem erweist sich jedoch als etwas komplexer, denn jede Saite schwingt für sich nicht nur auf dem Grundton, sondern auch in den Obertönen.
Bei der Verwendung von einfachem elastischen Stahldraht mit endlicher Dicke (nicht umsponnen) ändert sich die Ausbreitungsgeschwindigkeit der Wellen auf der Saite und zwar wellenlängenabhängig, denn bei kurzen Wellenlängen spielt die Federkraft des Drahtes eine vergleichsweise größere Rolle als bei langen. Somit variiert der Frequenzabstand der Obertöne untereinander.

Als Ergebnis kommt ein ungewöhnlicher Klang heraus, der bei periodischem Anstreichen der Saiten mit dem Finger ein sehr obertonreiches Spektrum besitzt und bei dem sich permanent die Aufteilung der Energie auf die Obertonfrequenzen verändert.

Diese Instrumente setzt man zur Therapie ein. Der ungewöhnliche Klang scheint beruhigend und ausgleichend auf Patienten zu wirken. In einer größeren Version gibt es dieses Instrument auch als Liege. Der Patient liegt oben, die Saiten sind unterhalb der Liegefläche angeordnet und übertragen ihre Schwingungen mechanisch direkt auf seinen Körper.
Da die Differenzfrequenzen auch im Bereich von wenigen Hertz erklingen, ist es denkbar, daß es sich hierbei um "Therapeutisches Entrainment" /Oschmann - 2009, S. 79 und S. 85/ handelt, nämlich das Synchronisieren von Prozessen in Gehirn und Körper.

Abb. 12: Ein besonderes Beispiel für gekoppelte Schwingungen zeigt dieser Monochord mit 20 gleichgestimmten Saiten, Saitenlänge zwischen den Stegen 105 cm. (Werner Reichel, Goslar).
Streicht man mit den Fingern ohne großen Druck periodisch quer über die Saiten, entsteht ein besonderer Klang. Alle Saiten schwingen gleichzeitig, sie tauschen dabei permanent Energie aus.
Der Klang besteht aus Grundton und einer Reihe von Obertönen, wobei einige Obertöne wechselweise lauter sind als andere. Dies hat Ähnlichkeit mit einem Obertongesang. www.oberton.org
Auch der Klang einer Maultrommel ist ähnlich, hierbei verändert man die Größe des Resonanzraumes im Mund und beeinflußt so die Klangfarbe, d.h. das Spektrum der Obertöne, vergleichbar mit der Bildung der Vokale beim Sprechen.
(FB)

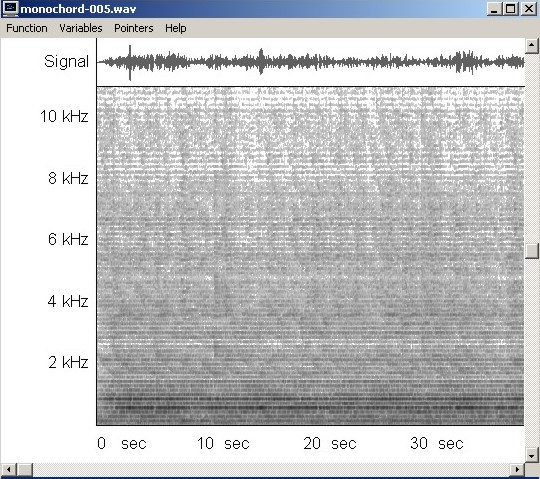Abb. 13: Frequenzanalyse des Klanges. Aufgetragen ist für eine Zeit von etwa 40 Sekunden die Intensität als Funktion der Frequenz. Je schwärzer die Fläche ist, um so stärker ist die zugehörige Frequenzanteil. frequenzanalyse
Bei der linearen Darstellung auf der Frequenzachse lassen sich aufeinanderfolgende Obertöne gut erkennen.
Die Frequenz eines Obertones ist ein ganzzahliges Vielfaches der Grundfrequenz, hier 141 Hz.

Auffallend, d.h. lauter, sind der vierte und sechste Ton (von unten), nämlich die Oktave und Quinte jeweils zur Oktave über dem Grundton.
Sie sind besonders stark, wechseln aber auch ihre Lautstärke unabhängig voneinander.
Die schrägen Streifen an vielen Stellen im Bild sind zeitlich mit dem Anregen durch die Finger korreliert.
Hier gibt es Veränderungen im Obertonspektrum.
Klangbeispiel (483 kB)
(FB)

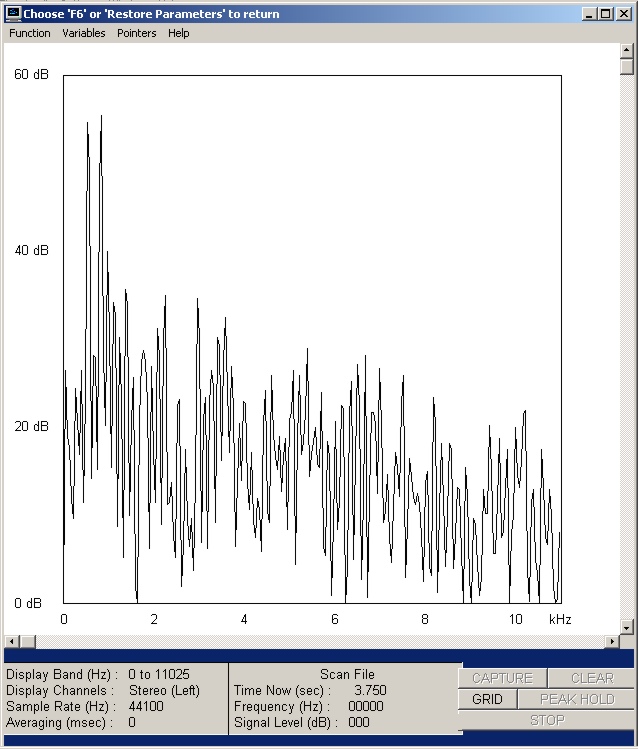Abb. 13a: Frequenzspektrum zur Zeit 3,75 Sekunde. (senkrechter Schnitt durch vorherige Abbildung bei dieser Zeit). Die vierte und sechste Ton ist besonders stark.
Bei etwa 10 kHz schwingt der 60. Oberton (FB)

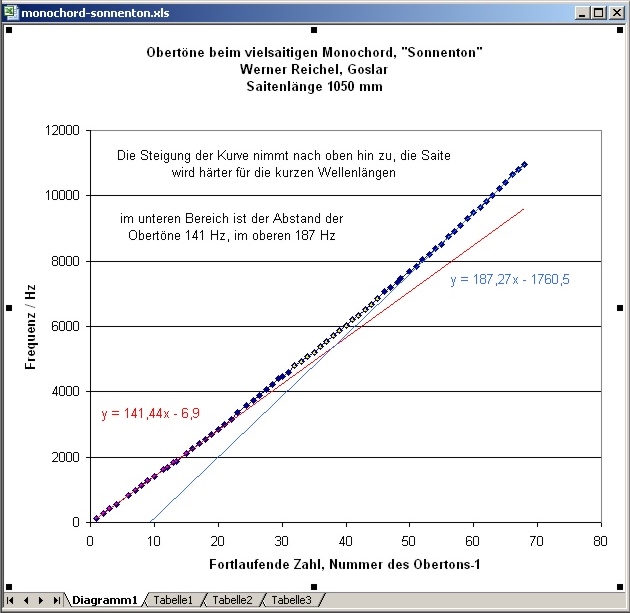Abb. 14: Bei stehenden Wellen auf einer Saite sind alle die Schwingungen erlaubt, für die die Wellenlänge ein ganzzahliger Bruchteil der Saitenlänge ist. stehende-welle
Bei konstanter Ausbreitungsgeschwindigkeit der Wellen auf der Saite bedeutet dies, daß die zugehörigen Frequenzen sich wie ganzzahlige Vielfache einer Grundfrequenz verhalten.

Bei diesem Monochord trift dies für die unteren Töne zu, allerdings bei den oberen nur eingeschränkt.
Für die oberen Tönen mit vergleichsweise kurzen Wellenlängen (Saitenlänge / Nummer des Tons ergibt die halbe Wellenlänge, z.B. 105 cm / 60 = 1,75 cm ) scheint die Saite eine größere Härte oder Biegesteifigkeit und damit eine höhrere Ausbreitungsgeschwindigkeit zu besitzen, denn der Biegeradius nimmt bei diesen kurzen Wellenlängen zu.
Im unteren Bereich haben die Obertöne einen Abstand von 141 Hz, im oberen einen von 187 Hz.
Das Verhältnis 187 / 141 beträgt 1,32.

Das Gemisch aus 20 nahezu gleich gestimmten Saiten mit leicht gegeneinander verstimmten Obertonreihen erzeugt eine bunte Vielfalt von Summen- und Differenzfrequenzen, die über den Klangkörper miteinander gekoppelt sind und permanent Energie untereinander austauschen.
Bei der Anregung unterbricht der Finger des Spielers kurzzeitig die Schwingung jeweils einer einzelnen Saite und erzeugt so unterschiedliche klangliche Muster.
(FB)

Abb: 15: Vielsaitiger Monochord, bespannt mit Schweißdraht 0,6 mm, W. Reichel, Goslar (FB)

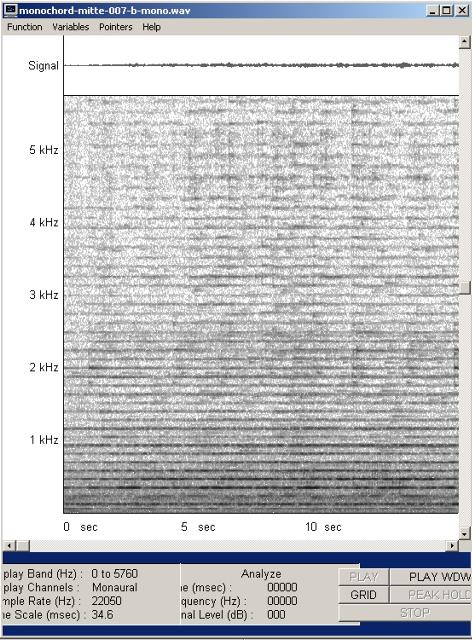Abb. 16: Klangspektrum,
Im Bereich von 1,5 bis 2,5 kHz sowie etwa bei 500 Hz lassen sich wellenförmige Bewegungen in der Lautstärke einzelner Obertöne beobachten.
Tondatei .WAV 360 kB (FB)

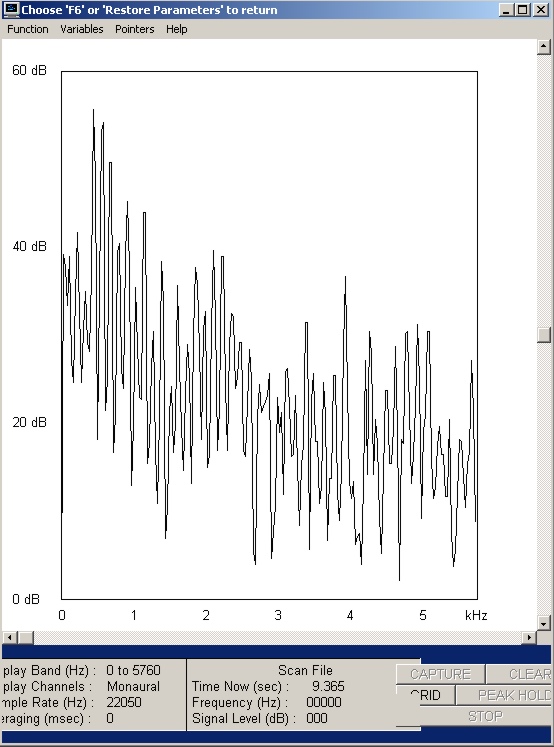Abb. 17: Spektrum der Obertöne (FB)

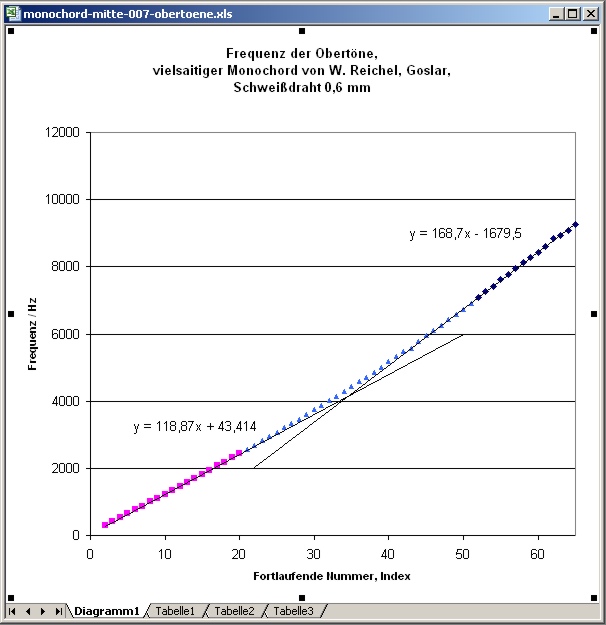Abb. 18: Der Abstand der Obertöne voneinander nimmt nach oben hin zu. Die Frequenz steigt stärker als die Vielfachen des Grundtones.
Die Anfangssteigung von 119 Hz (118,87) nimmt bei den oberen Tönen zu bis etwa 169 Hz (168,7) .
Das Verhältnis 167/119 beträgt 1,42.
(FB)

Zum Vergleich: Töne auf einer gestrichenen Saite (Cello) oberton-saite

Schwebungen zweier gekoppelter Saiten bei wellenlängenabhängiger Ausbreitungsgeschwindigkeit

Leicht gegeneinander verstimmte Saiten erzeugen beim Schwingen periodische Lautstärkenmodulationen Schwebung .
Wenn beispielsweise die eine Saite pro Zeiteinheit 100 Schwingungen macht und die andere 101, dann schwingen die beiden Saiten einmal pro Zeiteinheit exakt gleichsinnig und dazwischen mehr oder weniger gegensinnig, was sich als an- und abschwellender Ton bemerkbar macht.
Diese Aussage gilt nicht nur für den Grundton, sondern auch für die einzelnen Obertöne der Saiten. Beim Ton mit der doppelten Frequenz werden die Schwingungen bereits in der halben Zeit erreicht, so daß die Schwebungsfrequenz daher doppelt so hoch ist.

Wenn man mit seinen Ohren nun die Summe aller Teiltöne beider Saiten gleichzeitig wahrnimmt, dann läßt sich die Überlagerung aus der Schwebung der Grundfrequenzen und der Schwebung jeweils von Paaren ähnlicher Obertöne sowie der Mischfrequenzen unterschiedlicher Obertöne deuten.

Sofern die Abstände der Obertöne einer Saite immer den gleichen Abstand haben, sollte der wahrgenommene "Ton" der Schwebung ein einfaches Baumuster haben. Komplexer wird allerdings die Beschreibung der Überlagerung von zwei ähnlich gestimmten Saiten mit nach oben zunehmendem Obertonabstand. (Abb. 18)
Hier dürfte die Überlagerung von gemischten Obertönen eine Vielzahl von ähnlichen Frequenzen, nämlich ein breites Frequenzband erzeugen.

Abb. 19: Die erste und die letzte Saiten sind auf gleiche Frequenz gestimmt. Die erste wird durch Zupfen angeregt und die Schwingung der anderen aufgezeichnet. Die anderen Saiten sind etwa einen halben Ton (5%) höher und können daher nicht besonders stark mitschwingen.
Für die Aufnahme wird statt des Mikrofons (oben über den Saiten) ein magnetischer Tonabnehmer verwendet. Dieser verfolgt nur die Schwingung der letzten Saite.
(FB)

Abb. 20: Signal am magnetischen Tonabnehmer. Nach einer kurzen Anregung von wenigen Sekunden klingen die Saiten aus. (Möglicherweise ist der Verstärker an einigen Stellen übersteuert und produziert daher zusätzliche Obertöne.)
Tondatei (WAVE) 287 kB monochord
(FB)

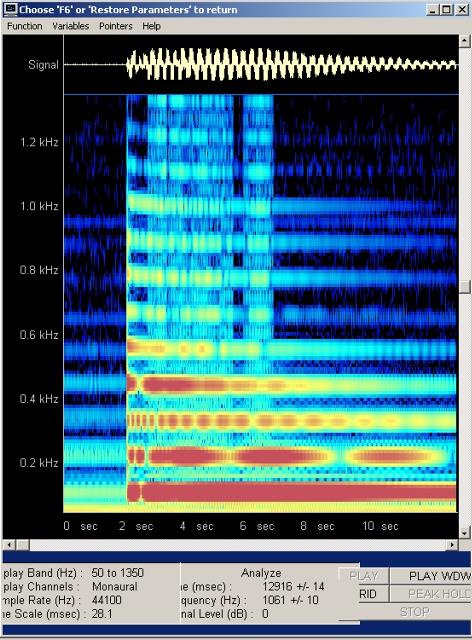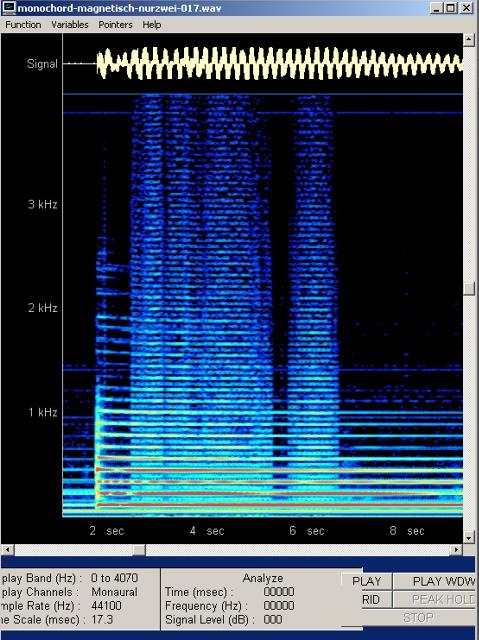
Abb. 21: Bei der Einstellung mit geringer Frequenzauflösung erscheinen die Spuren der Obertöne als breite horizontale Streifen breit. Hierbei wird besonders deutlich, daß die periodischen Lautstärkeveränderungen Schwebungen mit unterschiedlichen Frequenzen vorkommen.
Bei zwei idealen Saiten mit konstantem Obertonabstand und leichter Verstimmung nimmt die Schwebungsfrequenz proportional mit der Nummer des Tones zu.
In diesem Fall jedoch, mit ansteigendem Obertonabstand, hat beispielsweise die dritte Zeile von unten eine höhere Schwebungsfrequenz als die vierte.
(FB)

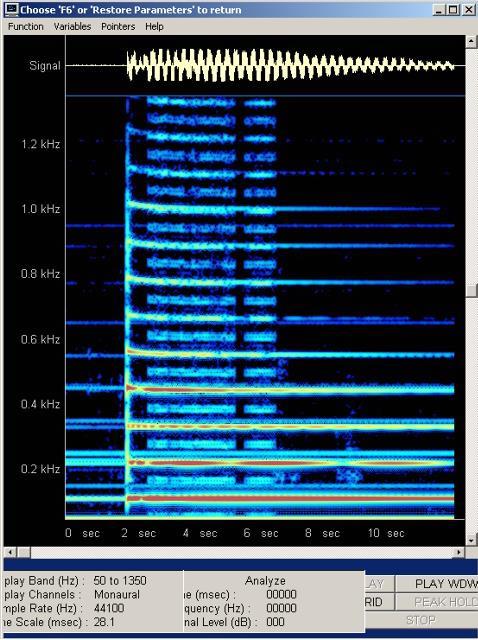Abb. 22: gleiche Daten, aber mit höherer Frequenzauflösung dargestellt. Die Zusatzspuren kommen von 50 Hz-Signalen aus der Netzspannung bzw. zwischen 3 und 7 Sekunden von der Übersteuerung des Verstärkers. (FB)

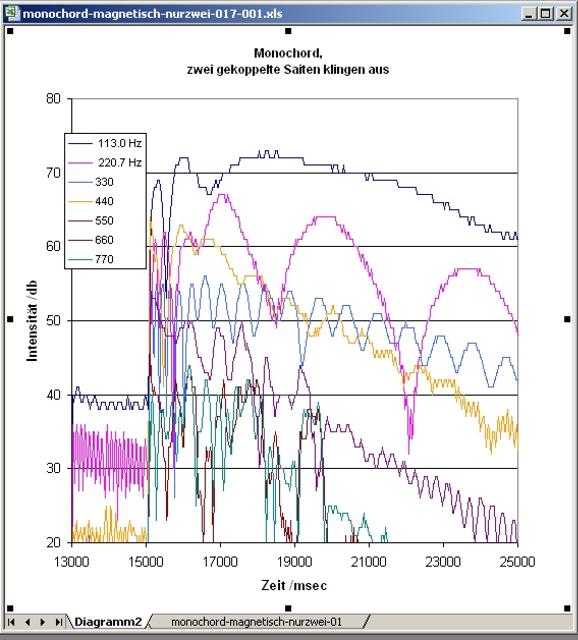Abb. 23: Zeitlicher Verlauf der Amplitude einzelner Frequenzen. Während die Kurve für 220 Hz wenige Schwingungen pro Zeit ausführt, sind es bei 330 Hz etwa 4 mal mehr. Erwartet würde der Faktor 3/2. (FB)