Friedrich Balck > Biosensor > Physik > Resonanz

Beobachtungen:

Resonanz, Frequenzmesser

Stößt man ein schwingungsfähiges Systeme einmalig an, dann wird es danach in der ihm eigenen Frequenz schwingen.
Beispiel: Kinderschaukel auf dem Spielplatz.

Die Schwingung wird nach einiger Zeit wieder zur Ruhe kommen, sofern keine weitere Energie hinzugefügt wird.
Soll die Schwingung trotz gewisser Energieverluste permanent erhalten bleiben, muß man ständig Energie nachliefern.
Bei der Kinderschaukel kann dies ein Außenstehender tun, der unregelmäßig aber zum richtigen Zeitpunkt die Schaukel kurz beschleunigt. Auch das Kind kann dies durch periodische Verlagerung des Schwerpunktes tun.

Immer dann, wenn das schwingende System im richtigen Zeitpunkt etwas Energie erhält, setzt sich die Schwingung trotz Reibung oder Dämpfung fort und kommt nie zur Ruhe.
Trifft die Energie zu falschen Zeiten ein, nützt sie nicht sondern kann der Schwingung sogar schaden, d.h. die Amplitude nimmt dann ab.

Bestimmt das schwingungsfähige System durch seine Parameter selber die Frequenz, etwa wie das Pendel einer Uhr oder ein Schwingquarz, dann hängt die Frequenz nur von diesen Parametern ab: Eigenfrequenz.
Man kann das System aber auch von außen mit einer (in gewissen Grenzen) beliebigen Frequenz anregen, dann schwingt es nach einer Einschwingzeit nur noch mit dieser äußeren Frequenz: erzwungene Schwingung.
Die Zeit, die das System braucht, um sich auf die Anregefrequenz einzustellen, hängt von der Größe der Dämpfung ab.
schwebung    Bei geringer Dämpfung dauert es sehr lange.

Die sich dabei einstellende Amplitude kann bei geringer Dämpfung im Bereich der Eigenfrequenz extrem große Werte annehmen. Weit außerhalb der Resonanzfrequenz ist die Amplitude sehr klein. (Abb. 07)

Regt man mit der Eigenfrequenz an, nimmt bei fehlender Dämpfung die Amplitute bei jeder Schwingung zu. Sie kann theoretisch den Wert unendlich erreichen. Doch meist schon vorher gibt es Grenzen, die durch die hohen Belastungen unter Umständen das System zerstören. Resonanzkatastrophe

Diesen Effekt mit den großen Amplituden bei der richtigen Frequenz nutzt man aus, um Frequenzen zu messen: denn nur, wenn bei einem schwingungsfähigen System Energie mit der richtigen Frequenz angeboten wird, kommt es zu einer starken Schwingung. Im anderen Fall ist sie kaum merkbar.

Vor der Zeit der elektronischen Meßgeräte waren mechanische Frequenzmesser die einzigen verwendbaren Systeme. (Abb. 01)

Anwendung: Gut abgestimmte Antennen arbeiten mit hohem "Gewinn".
Die Funkwellen koppeln bei der Resonanzfrequenz besonders gut an die Antenne an.   antenne

Beispiel für Ausnutzung der Resonanz zur Energieübertragung:
Teslas Energieübertragung über viele Kilometer:     tesla

Die Amplitude, die sich bei äußerer Anregung im Bereich der Resonanzfrequenz einstellt, hängt von der Dämpfung ab.
Je geringer die Dämpfung ist, um so mehr steigt die Amplitude an. Resonanzüberhöhung

Will man trotz vorhandener Dämpfung eine besonders große Amplitude bekommen, dann muß man die verloren gehende Schwingungsenergie permanent ersetzen. Diese Überlegung erscheint zunächst als unsinnig.
Doch dieses Verfahren ist durchaus nützlich bei den ersten Radioempfängern gewesen (Rückkopplungsempfänger).
Die an der Antenne ankommende sehr geringe Spannung sollte mit wenigen Mitteln kräftig verstärkt werden.

Der benutzte elektrische Verstärker war auf die Empfangsfrequenz eingestellt und hatte einen Verstärkungsfaktor von etwas unter 1, d.h. ganz knapp unterhalb der Schwelle, bevor er selber sich zum Schwingen anregt. Damit war die Dämpfung nahezu aufgehoben. Die Verstärkung des Signals erfolgte im Prinzip also passiv durch Resonanzüberhöhung und nicht durch einen aktiven Verstärker.   Audion

Mit diesem Trick bekommt man sehr hohe Empfindlichkeiten, denn jede im richtigen Takt zugeführte Energie erhöht die Amplitude.
Allerdings erkauft man sich dadurch auch Nachteile: große Zeitkonstante, sehr hohe Frequenzabhängigkeit.

Resonanzen findet man auch in der Spektroskopie von Elektromagnetischen Wellen.
Absorptionslinien
Im Spektrum des Sonnenlichts sind dunkle Linien zu beobachten, die so genannten Fraunhofer-Linien. Sie kommen daher, daß das ausgestrahlte Licht auf dem Weg zur Erde beispielsweise von Eisen-Atome absorbiert wird.
Diese Atome geben das Licht zwar wieder ab, allerdings nicht nur in ursprünglicher Richtung sondern auch in andere.
Daher ist die Intensität in der ursprüglichen Richtung vermindert.

Mössbauerlinien
Es gibt radioaktive Atome, bei denen ein Teil der Gammastrahlung besonders rein ist bezüglich der spektralen Breite, wenn die Atome in einem Festkörper eingebunden sind. (Mößbauerlinien)
Sie können diese Strahlung abgeben aber auch aufnehmen, man spricht von Resonanzfluoreszenz. (Die Energie wird passend geliefert und auch komplett aufgenommen.) Somit ist es möglich, daß gleichartige Isotope mit ihren Gamma-Quanten (theoretisch "permanent") Energie austauschen.

Würde man zwei Atome so miteinander koppeln, daß die Gamma-Quanten gerichtet zum Partner ausgesendet würden, hätte man
so etwas wie bei einem vergleichbaren mechanischen System: gekoppelte Pendel. gekoppelt


Abb. 01: Über die Resonanz von Federzungen, lassen sich unbekannte Frequenz bestimmen. Regt man beispielsweise alle Stahl-Zungen gleichzeitig mit einem Elektromagneten an, dann schwingen die besonders stark, deren Frequenz in der Anregung enthalten ist. Resonanz bei 51,5 Hz. (FB)	Abb. 02: Resonanz bei 48 Hz (FB)

Abb. 03: Helmholtzresonator. Volumen und Querschnitt der Öffnung bestimmen die Resonanzfrequenz. (FB)	Abb. 04: Helmholtzresonator. Die große Öffnung bestimmt die Resonanzfrequenz, die kleine führt man in den Gehörgang ein, um die Lautstärke im Holhraum zu verfolgen. (FB)

Abb. 05: Ein Jagdhorn ist mit Sender (Ohrhörer im Mundstück) und Empfänger (Mikrofon im Schalltrichter) ausgestattet. Stimmt man die Senderfrequenz durch (Sweep) , dann erhält man bei den Resonanzfrequenzen (Obertöne) besonders laute Töne. (FB)

Abb. 06: Ein einfaches Kunststoffrohr wird mit einem kleinen Kopfhörer an einem Ende akustisch angeregt. Ein Mikrofon am anderen Ende nimmt die Lautstärke auf (vergleichbar mit vorheriger Abbildung). Dargestellt ist über der Frequenz das Verhältnis von abgegebener zu eingestrahlter Lautstärke. Es sind deutlich mehrere Resonanzen bei unterschiedlichen Frequenzen zu beobachten (Obertöne) frequenz-analyse (FB)

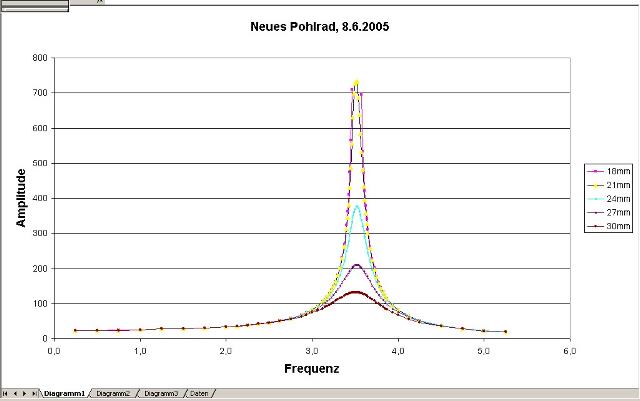
Abb. 07: Erzwungene Schwingung, Anregung mit einem Motor. Resonanzkurve eines mechanischen Schwingers (Masse + Feder). Bei Anregung mit einer Frequenz von ungefähr 3,5 Hz führt dieses System starke Schwingungen aus. Je nach Dämpfung sind die Ausschläge mehr oder weniger stark. Bei Anregung weit außerhalb der Resonanzfrequenz ist kaum eine merkliche Bewegung zu beobachten. (Clausthaler Drehpendel)(FB)

Abb. 08: Resonanztopf für Mikrowellen. Ein mechanischer Hohlraum, dessen Größe mechanisch auf die Wellenlänge abgestimmt wird. Als Antennenleitung werden Hohlleiter mit rechteckförmigem Querschnitt verwendet. stehende (FB)

Abb. 09: Ein Stimmgabel ist physikalisch gesehen, ein schwingungsfähiges System mit einer festen Eigenfrequenz. Man kann sie einerseits zur Wiedergabe dieser Frequenz nutzen durch Anschlagen oder andererseits auch als Detektor nehmen. Wird sie von außen mit ihrer Eigenfrequenz angeregt, fängt sie an zu schwingen. Die Amplitude ist dann beispielsweise fühlbar. (FB)

Abb. 09a: Technische Anwendung: In Quarz-Uhren nutzt man ein ähnliches geformtes Bauelement aus Quarz, dessen Resonanzfrequenz auf 2^15 = 32768 Hz abgestimmt ist. Es ist nur wenige Millimeter groß. Man kann es als Taktgeber oder aber auch als Signalquelle und damit als Detektor für Gase nutzen. Schießt man nun mit dieser Frequenz einen feingebündeltem Laserstrahl zwischen die Zinken und erwärmt die Gasmoleküle dazwischen, dann fängt die Gabel an zu schwingen. An den elektrischen Kontakten ist dann eine Wechselspannung zu messen. QEPAS quartz enhanced photo acoustic spectroscopy (AP)

Abb. 10: elektrisch erregte Stimmgabel, Antrieb über "Wagnerschen Hammer" wie bei einer Klingel (FB)	Abb. 11: Radioempfänger, Kristalldetektor (Gleichrichter), Spule und abstimmbarer Kondenstator (FB)

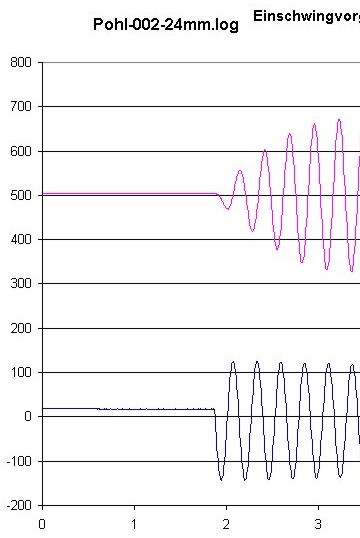
Abb. 12:Einschwingvorgang einer erzwungenen Schwingung in der Nähe der Resonanz: Verlauf der Bewegung als Funktion der Zeit. Erzwungene Schwingung (oben), Anregung (unten) Die Amplitude nimmt linear mit der Zeit zu. (Nur am Anfang. Danach kommt es in diesem speziellen Fall zu einer Schwebung, weil die Resonanzfrequenz nicht exakt eingestellt war. schwebung ) (FB)

Abb. 13: Ein Glasgefäß enthält etwas Natrium. Heizt man es auf etwa 250 Grad auf, dann verdampft das Natrium. Seitliche Beleuchtung mit der Taschenlampe zeigt, daß das Licht oben ungehindert durch den Dampf geht. (FB)	Abb. 14: Verwendet man Licht einer Natriumdampflampe, dann wird der Dampf zum Leuchten angeregt. Man kann durch das Gefäß nicht mehr hindurch sehen. Resonanzabsorption Die Dampfatome nehmen die passende Energie auf, geben sie anschließend wieder ab, aber streuen sie in alle Richtungen - auch in Richtung der Kamera. (FB)