Friedrich Balck > Biosensor > Physik > Wellen

Beobachtungen:

Wellen, Ausbreitungsgeschwindigkeit, Wellenlänge

1.1 Wasserwellen
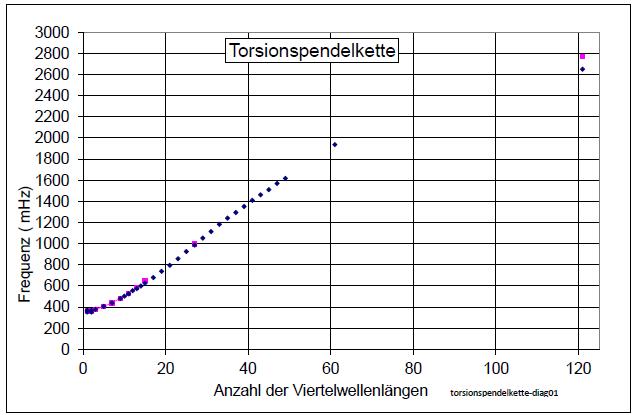
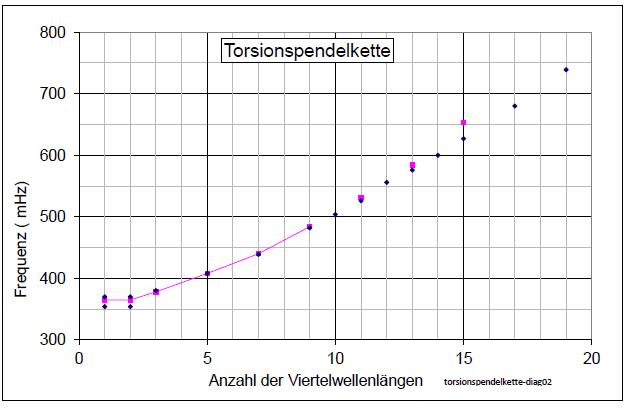
1.2 Torsionspendelkette
1.3 Wellen im Metallstab, Schallgeschwindigkeit
1.3.1 Soliton, Wellenpaket
2.1 Ausbreitungsgeschwindigkeit in einem wassergefüllten Schlauch
2.1.1 Soliton, Wellenpaket
2.2 Seilwelle
2.3 Wellenwiderstand bei einer elektrischen Leitung
2.4 Wasserwellen in Kanälen unterschiedlicher Breite
2.5 Wellenwiderstand, Nachbildung durch Kapazitäten und Induktivitäten
2.6 Abschlußwiderstand bei Lecherleitung für Mikrowellen
2.7 Wellenwiderstand, Abschlußwiderstand bei einem Koax-Kabel

Als Wellenlänge bezeichnet man den Abstand zwischen zwei Wellenbergen bzw. -tälern.
Die Anzahl der Schwingungen pro Sekunde nennt man Frequenz.

Wellen haben eine Ausbreitungsgeschwindigkeit.
Beispiel: für die beiden unterschiedlichen Wellenarten Licht und Schall sind es Licht- beziehungsweise Schallgeschwindigkeit.

Doch nicht nur die Art der Welle, sondern auch das Material, in dem sich die Wellen ausbreiten, hat einen Einfluß auf deren Ausbreitungsgeschwindigkeit.
In der Optik nutzt man diese Abhängigkeit aus, um beispielsweise mit einem Glasprisma die Farben des weißen Lichtes in seine Bestandteile zu zerlegen. Rotes Licht hat eine andere Ausbreitungsgeschwindigkeit als blaues.
(Dispersion) dispersion . Auch mit einem Gitter läßt sich die Verteilung der Wellenlängen sichtbar machen. lichtzerlegung

Das Produkt aus Wellenlänge L und Frequenz f ergibt die Ausbreitungsgeschwindigkeit c.     c = L * f

Normalerweise findet bei der Ausbreitung von Wellen ein Energietransport (nicht Massentransport) statt. Es gibt aber auch besondere Wellen, die stehenden Wellen, bei denen zwei Wellen gleicher Eigenschaft aufeinanderzulaufen und sich überlagern.
Hier verschwindet der Energietransport, weil in der Summe die Transporte in entgegengesetzten Richtungen sich aufheben.
stehende-welle

Durchläuft die Welle einen Bereich, in dem das Medium für die Ausbreitung andere Eigenschaften hat, dann kommt es in der Regel zu Reflexionen. Hierbei ändert ein Teil oder die gesamte Welle ihre Ausbreitungsrichtung. spiegelung

Was bei optischen Spiegeln gewünscht ist, kann bei der Weiterleitung von hochfrequenten Wellen in einem Kabel unerwünscht sein, wenn beispielsweise an einer schlecht konstruierten Verbindungsstelle zweier Kabelstücke ein Teil der Energie wieder zurückfließt. Für ungehinderte Ausbreitung, d.h. ohne Reflexionen, sollte der Wellenwiderstand einer Leitung überall gleich sein.
Diese Größe ist konstruktionsbedingt und ergibt sich aus den geometrischen Abmessungen sowie aus den Materialeigenschaften der Leitung.

In diesem Sinne muß auch das Ende einer Leitung "unsichtbar" sein, wenn die dorthin fließende Welle nicht wieder zurückreflektiert werden soll, d.h. der Verbraucher oder Empfänger muß für die Welle den gleichen Widerstand wie den Wellenwiderstand der Leitung haben.
In Antennendosen baut man zu diesem Zweck einen "Abschlußwiderstand" ein. Für die Welle erscheint dann die Leitung so, als wäre sie unendlich lang. Denn unendlich lang bedeutet: es dauert unendlich, bis ein Echo zurückkommt, also nie!

Mit anderen Worten, damit es nicht zu Reflexionen kommt, muß der Empfänger im optimalen Fall die Energie von der Leitung komplett übernehmen. Man nennt diesen Zustand Anpassung.

Leitung mit einheitlicher Eigenschaft

                               Sender=====================================Empfänger

Leitungen mit wechselnden Eigenschaften erzeugen Reflexionen

                                Sender==================----------------------Empfänger

Energieverluste treten auf dem Weg vom Sender zum Empfänger auf, wenn beispielsweise ein Teil der Energie in Wärme oder andere Strahlung umgewandelt wird oder die Leitung auch seitlich abstrahlt.
Im Fall von Reflexionen geht die Energie nicht verloren, sie kommt nur nicht beim Empfänger an. Der Sender wird sie nicht los, weil sie dorthin wieder zurückkommt.

Dualismus Welle-Teilchen

Teilchen erzeugen Wellen, Wellen bewegen/erzeugen Teilchen Welle-Teilchen

Eigenschaften von Wellen:

Schwingungsrichtung in Richtung der Ausbreitung oder dazu senkrecht,
longitudinal bzw. transversal.

Damit sich eine Welle ausbreiten kann, muß permanent ein Austausch zwischen zwei unterschiedlichen Energiespeichern stattfinden.

Schallwellen
in Gasen, Flüssigkeiten und Festkörpern
Es bewegen sich gekoppelte Masseteilchen um eine Ruhelage, dabei findet ein ständiger Wechsel
    von Lage- und Bewegungsenergie ab.
(Beispiel: Feder-Masse-System, hier wirkt die Feder als rückstellende Kraft)

Elektromagnetische Wellen
in Vakuum, Gasen, Flüssigkeiten und Festkörpern
Es ändern sich permanent elektrisches und magnetisches Feld im Wechsel, damit gibt es einen ständigen Austausch
   von elektrischer und magnetischer Energie.

Alfvén-Wellen
Wellen durch Kopplung von mechanischen mit elektromagnetischen Energien:
geladene Masseteilchen bewegen sich im Magnetfeld, dabei wirkt das Magnetfeld als rückstellende Kraft (magneto-hydrodynamische Wellen, Alfvén-Wellen)

????? weitere Wellen
        geladene Masseteilchen im elektrischen Feld,
        Ladungsverschiebung durch mechanische Kraft, Piezo-Effekt,
        Magnetfeld bewirkt Verschiebung von magnetischen Atomen, Magnetistriktion

Verknüpfung unterschiedlicher physikalischer Eigenschaften/Größen zu Wellen

Darstellung der Wechselwirkung untereinander

rot: Schulbuchphysik


	elektrisch	magnetisch	akustisch	Schwerkraft	Teilchen aus Weltall (Kosmos)	Teilchen aus der Erde
elektrisch	Skalarwellen?	elektro- magnetisch	im Festkörper: piezoelektrisch	?	?	?
magnetisch		?	im Gas: Alfven-Wellen, im Festkörper: Magnetostriktion	?	?	?
akustisch			Schall	?	?	?
Schwerkraft				Schwerkraft- wellen?	?	?
Teilchen aus Weltall (Kosmos)					kosmische Teilchen, Sonnenwind, . .	?
Teilchen aus der Erde						Radioaktivität, Zerfall

1.1 Wasserwellen


Abb. 01-01: Wasserwellen treffen schräg auf einen Uferstreifen. Die abnehmende Wassertiefe beeinflußt die Ausbreitungsgeschwindigkeit. Dabei ändert sich bei gleichbleibender Frequenz die Wellenlänge. (FB)

Abb. 01-02: Eine bisher geradlinige Wellenfront im tiefen Wasser bekommt bei schräger Annäherung an das Ufer eine gekrümmte Kontur. Man sagt, die Wellen werden (in ihrer Richtung) gebrochen. Wellen im flachen Wasser in Ufernähe laufen langsamer als die Wellen im tieferen Wasser. (FB)

Abb. 01-03: Ein Boot hinterläßt ein Wellenfeld. Die Wellen breiten sich mit unterschiedlicher Geschwindigkeit aus. Für große Wellenlängen gilt: Wellen mit großer Wellenlänge sind schneller als solche mit kurzer. Am Ende bleibt offensichtlich eine Welle mit kleiner Wellenlänge (rechts im Bild) übrig. (FB)

Abb. 01-3a:	Abb. 01-3b:
Eine kurze Anregung durch zwei Luftströme mit Paketen aus mehreren schnellen Schwingungen auf eine Wasseroberfläche löst zwei Systeme von Kreiswellen aus, die sich überlagern. Das Interferenzmuster in der Mitte mit den kleinen Wellenlängen hat sich schon eingestellt bevor die Wellen mit den großen Wellenlängen diese Region erreicht haben. Abstand der Blasdüsen etwa 8 Zentimeter. Bei sehr kleinen Wellenlängen macht sich der Einfluß der Oberflächenspannung bemerkbar und die Ausbreitungsbeschwindigkeit ändert sich in umgekehrter Weise wie oben. Für sehr kleine Wellenlängen gilt: Wellen mit kleiner Wellenlänge sind schneller als solche mit großer. (FB)

Abb. 01-04: zwei Enten schwimmen auf dem Wasser. Sie erzeugen eine Bugwelle. (FB)	Abb. 01-04a: Die Bugwelle besteht aus kleinen Wellen, deren Ausbreitungsrichtung aber nicht mit der der Bugwelle übereinstimmt. (FB)

Abb. 01-05: Wellenwanne und Schwimmmer (Tucke) aus dem Anglerbedarf. (FB)

Abb. 01-05a: Die Schwimmkörper folgen der Neigung der Oberflächen. Sie zeigen damit an, daß auch unterhalb der Oberfläche das Wasser seitlich hin und her strömt. (FB)

Abb. 01-05b: Wasseroberfläch und Schwimmkörper, die Wellenberge sind spitzer als die Täler. (FB)

Abb. 01-05c: Lautsprecher mit dünnem Rohr und Styropor-Verdränger als Wellengenerator, Frequenz im Bereich von etwa 2 Hz. (FB)

Abb. 01-05d: Die Ostsee ist ruhig? Geringer Wind erzeugt kleine Wellen mit kurzer Reichweite. Die sich diagonal durch das Bild ziehende lang ausgedehnte Welle könnte von Schiffen oder vorheriger Dünung stammen. . . . Original date/time: 2008:05:03 10:33:36 (FB)

Abb. 01-05e: . . . und es gibt noch größere (bezüglich Wellenlänge, Periodendauer) Wellen: Im Vergleich zum vorherigen Bild ist der Wasserstand hier rund 20 cm tiefer. Zeitlicher Abstand der Bilder: etwa 100 Sekunden. Original date/time: 2008:05:03 10:31:50 (FB)

1.2 Torsionspendelkette

Abb. 01-06: Abb. 02-13: Torsionspendelkette Entlang der Strecke befindet sich ein gespannter Stahldraht ( Klaviersaite) an dem die einzelen Pendel befestigt sind. Über den Draht sind die Pendel miteinander gekoppelt. (FB)

Abb. 01-06a: Abb. 02-14: Torsionspendelkette in Ruhe, rechts ein Aluminiumring zwischen den Polen eines Elektromagneten zur einstellbaren Dämpfung (Wirbelstrombremse), über den Gleichstrom einstellbar. Diese Bremse wirkt wie der Abschlußwiderstand bei einer Leitung. Bei korrekter Einstellung gibt es keine Reflexionen. (FB)

Abb. 01-06b: Torsionspendelkette, demonstriert das Entstehen und Verhalten von Wellen. (FB)	Abb. 01-06c: Eine Reihe von kleinen Pendeln ist auf einer durchgehenden Torsionsfeder (Stahldraht) angebracht. Jedes Pendel kann mit Hilfe dieser Feder einen Teil seiner Energie auf das Nachbarpendel übertragen. (FB)


Abb. 01-06d: Bei einer Welle bleiben die Schwinger an ihrer Position, der Ort mit dem größtem Ausschlag verschiebt sich mit der Zeit. (in Richtung Kamera) (FB)	Abb. 01-06e:Die Pendelkette in Bewegung. Vier Bilder jeweils rund 0,2 Sekunden nacheinander aufgenommen. (FB)

Abb. 01-07: Ein Scheibenläufermotor bildet das Endlager des Torsionsdrahtes läuft sehr leicht, Drehzahl ist proportional zur Spannung Der Aluminiumstab auf dem Vierkant sorgt für eine mechanische Begrenzung bei der Anregung. (FB)

Abb. 01-08: Torsionspendelkette, angeregt mit Scheibenläufermotor, am hinteren Ende festgelegt. Einige Schwingungen sind: fest-fest (10,12,14), die meisten: fest-lose Anregung mit Frequenzgenerator plus Sinusgenerator mit DA-Wandler (H. N.) Es gibt 62 Pendel Bei tiefster Frequenz gibt es zwei Zustände: Knoten-Bauch-Knoten und Knoten-Bauch, wechselnd im Zeitraum von mehreren Minuten alter Draht 28.5.2004 / neuer Draht 23.6.2004 Anzahl: 61 1937 mHz Jedes zweites Pendel steht

Abb. 01-09: Frequenzen der stehenden Wellen mit altem Draht (blau), neuem Draht (rot) Die Frequenzen folgen nicht genau dem Vielfachen einer Grundfrequenz. (FB)

Abb. 01-09a: im unteren Frequenzbereich gibt es stehende Wellen mit Viertelwellenlängen. Im unteren Frequenzbereich ist die Kurve nicht linear. (FB)

1.3 Wellen im Metallstab, Schallgeschwindigkeit

1.3.1 Soliton, Wellenpaket

siehe auch stehende-welle.htm#eisenstab

Abb. 01-20: Mehrere Stäbe aus Metall. Holz und Kunststoff liegen auf dem Tisch.
Dazu gibt es zwei Piezo-Druckaufnehmer und einen kleinen Hammer zum Anschlagen der Stäbe. (FB)

Abb. 01-21: Der Aluminiumtab steht auf dem Druckaufnehmer, von oben wird mit dem Hammer geklopft.
Dieser Impuls breitet sich nach unten aus, wird reflektiert usw. bis die Energie aufgezehrt ist. (FB)

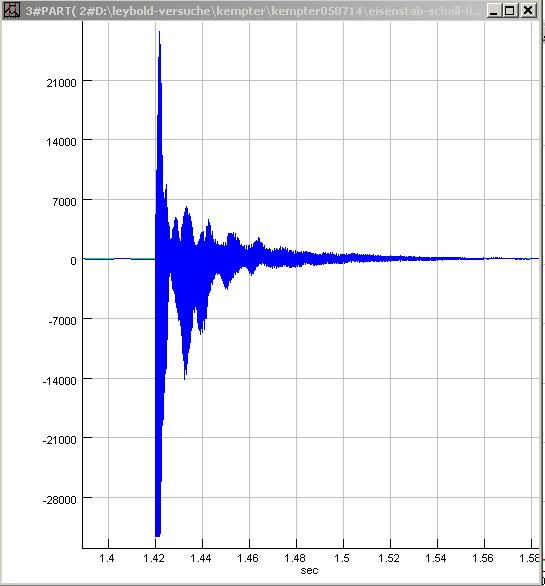Abb. 02-22: gemessenes Signal bei dem Eisenstab.
eisenstab-schall-001.wav (FB)

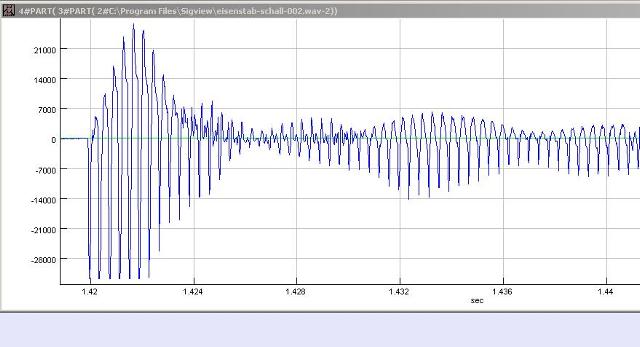Abb. 02-22a: gemessenes Signal bei dem Eisenstab.
eisenstab-schall-001.wav (FB)

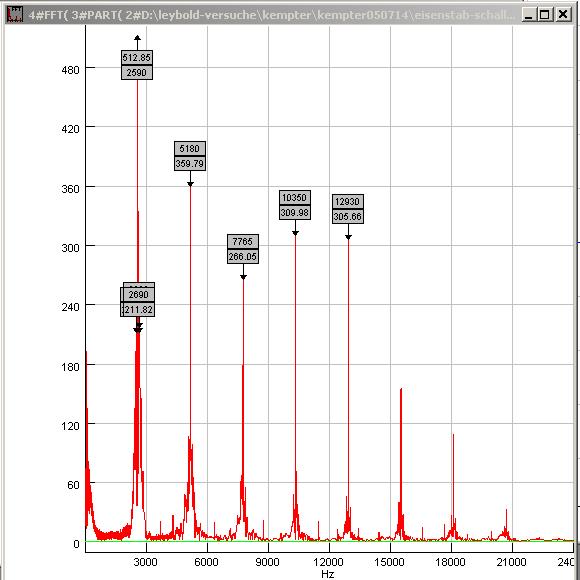Abb. 02-23: Frequenzanalyse: Es gibt Harmonische bei 2590 Hz, 5180 Hz, 7765 Hz, 10350 Hz
12930 Hz usw.
eisenstab-schall-001.wav (FB)

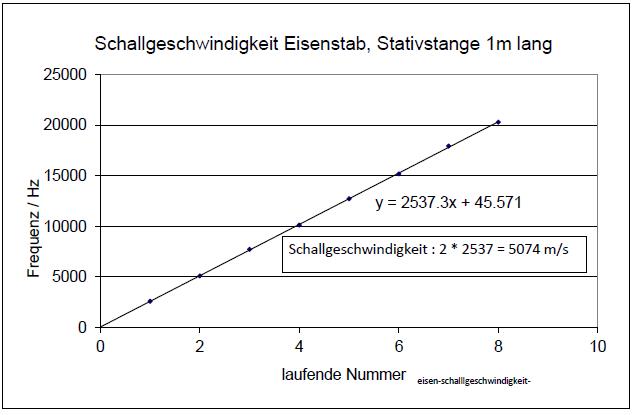Abb. 02-24: Die Frequenzen der Harmonischen aufgetragen ergeben eine Gerade.
Aus der Steigung folgt für die Schallgeschwindigkeit (Hin- und Rückweg: Faktor 2) 5074 m/s
eisenstab-schall-001.wav (FB)

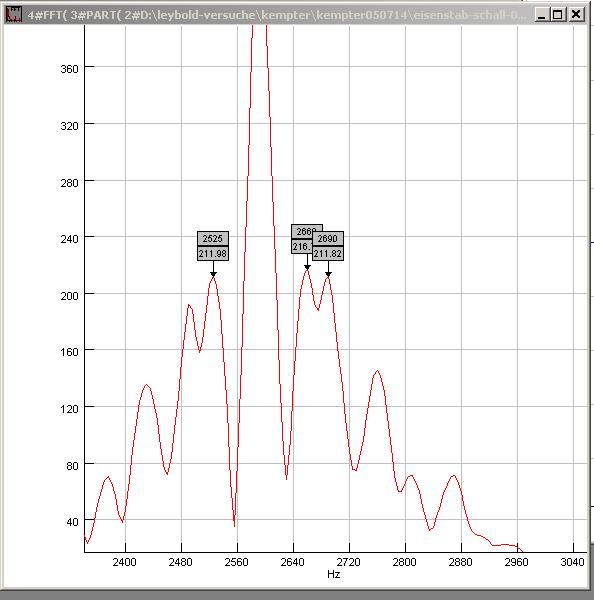Abb. 02-25: Erster Peak. Es gibt weitere Schwingungen im Abstand von rund 30 und 60 Hz.
2525 2590 2660 2690 (Biegeschwingung?)
eisenstab-schall-001.wav (FB)

zum Vergleich Schallgeschwindigkeit in einem akustischen Rohr blechblasinstrument-00.htm#kapitel-00-00-01

2.1 Ausbreitungsgeschwindigkeit in einem wassergefüllten Schlauch

Ein 10 Meter langer PVC-Plastikschlauch (4 mm Innendurchmesser) liegt auf dem Boden.
Er ist mit Wasser gefüllt. An beiden Enden ist jeweils ein Drucksensor angebracht.
Schlägt man mit der Kante eines Holzbrettes auf den Schlauch, breitet sich in beiden Richtungen eine Welle aus.

Wenn der Aufschlagpunkt in der Mitte ist, sind die Laufzeiten bis zu den Sensoren gleich lang.
Ist er nicht in der Mitte, dann kann man aus den unterschiedlichen Laufzeiten der Signale die Ausbreitungsgeschwindigkeit bestimmen.

In diesem Beispiel beträgt die Ausbreitungsgeschwindigkeit 57 m/s

Strecke / m	Laufzeit / s
0	0
1	0.015
2	0.032
3	0.052
4	0.069
5	0.088
6	0.102

2.1.1 Soliton, Wellenpaket

Abb. 02-01: PVC-Plastikschlauch (4 mm Innendurchmesser) ist wassergefüllt. An jedem Ende ist ein Drucksensor angebracht. (FB)

Abb. 02-02: Mit der Kante dieses Brettes wird ein Impuls auf die Flüssigkeit gegeben. (FB)

Abb. 02-02a: Hinter den beiden Messingzylindern sitzen Druckaufnehmer, Meßbereich 250 mmWS (FB)

Abb. 02-02b: MicroSwitch, Differenzdrucksensor, 395-241 (FB)

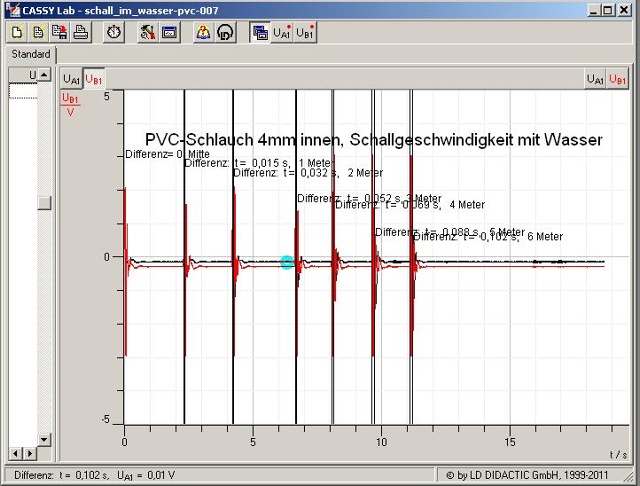Abb. 02-03: Signale an den Drucksensoren: rot: linke Strecke und schwarz: rechte Strecke
schall_im_wasser-pvc-007.lab (FB)

Abb. 02-04: Startposition ist in der Mitte, Laufzeit 0.0 s
rot: linke Strecke, schwarz: rechte Strecke (FB)

Abb. 02-05: Strecke 1 m, Laufzeit 0.015 s (FB)

Abb. 02-06: Strecke 4 m, Laufzeit 0.69 s (FB)

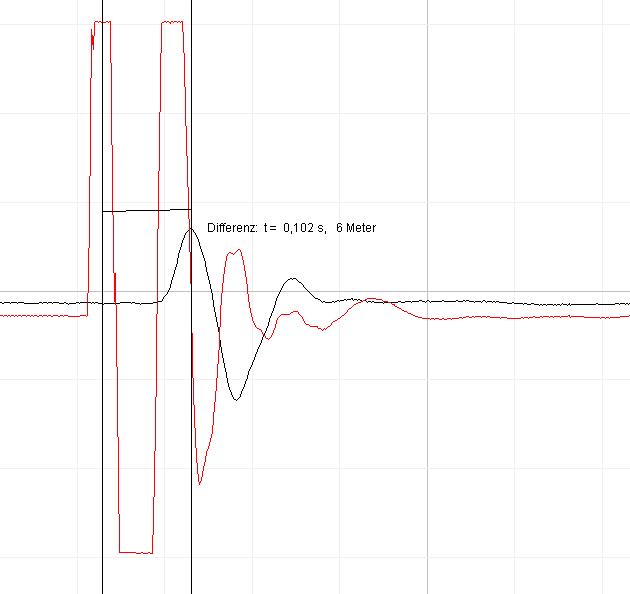Abb. 02-07: Strecke 6 m, Laufzeit 0.102 s (FB)

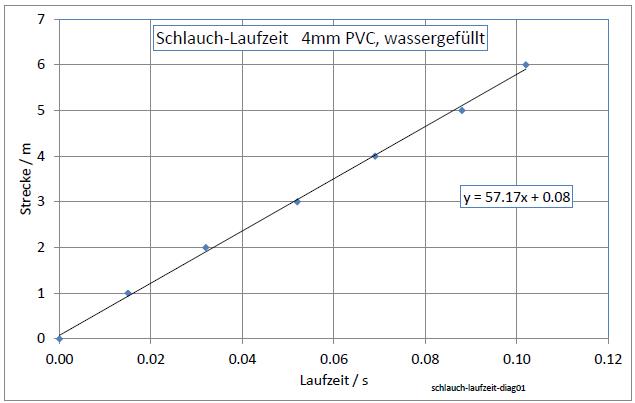Abb. 02-08: Die Ausbreitungsgeschwindigkeit beträgt 57 m/s. (FB)

2.2 Seilwelle
Ausbreitungsgeschwindigkeit v =   Wurzel aus (Zugspannung / Materialdichte)

v = Wurzel aus ( Kraft/Fläche / Masse / Volumen)

v = Wurzel aus (Kraft / Masse pro Fläche*Länge/Fläche)    = Wurzel aus (Kraft / Masse pro Länge)

Abb. 02-09: seitlich angestoßenes Wellenpaket auf dem Seil eines Skiliftes (FB)

Abb.02-10: Schraubenfeder, senkrecht aufgehängt. Hier kann man gut sichtbar Wellenpakete von einem Ende zum anderen laufen lassen.
Allerdings ändern sich die Eigenschaften während der Ausbreitung, da die Feder durch das Eigengewicht oben stärker gedehnt ist als unten. (FB)

Abb.02-10a: Solitone auf einem Seil, Computeranimation
Seilwelle, mit Impuls ohne Ende
https://www.edumaps.de/media/phet/wave-on-a-string_de.html

stehende-welle.htm

Abb. 02-11: Ein Gummiseil wird periodisch angeregt. Es bildet sich eine stehende Welle.
stehende-welle.htm (FB)

Abb. 02-12: Ein dünner Draht ist zur Form einer Glocke gebogen. Er wird in der Mitte periodisch angeregt. Es bilden sich stehende Wellen aus. An den beiden unteren Enden ist jeweils ein Schwingungsbauch. Bei der Anregung oben ist ein Knoten. (Beim akustischen Rohr wäre dies ein offenes Ende und ein geschlossenes Ende)
stehende-welle.htm (FB)

Abb. 02-13: Torsionspendelkette wie in Abb. 01-06 bis 01-09
Entlang der Strecke befindet sich ein gespannter Stahldraht ( Klaviersaite) an dem die einzelen Pendel befestigt sind. Über den Draht sind die Pendel miteinander gekoppelt. (FB)

Abb. 02-14: Torsionspendelkette in Ruhe, rechts ein Aluminiumring zwischen den Polen eines Elektromagneten zur einstellbaren Dämpfung (Wirbelstrombremse), über den Gleichstrom einstellbar.
Diese Bremse wirkt wie der Abschlußwiderstand bei einer Leitung.
Bei korrekter Einstellung gibt es keine Reflexionen. (FB)

Abb. 02-15: Eine Gassäule in einem Rohr wird an einem Ende mit Schallwellen aus einem Lautsprecher angeregt. (Dort ist das Rohr mit einer elastische Folie abgeschlossen.) Dadurch läßt sich der Druck im Rohr ortsabhängig verändern. Die Länge der Flammen zeigt an, wie groß der aktuelle Druck gerade ist. So lassen sich stehende Wellen im Rohr sichtbar machen. Rubens'sches Flammenrohr. (FB)

2.3 Wellenwiderstand bei einer elektrischen Leitung

Bei einer zweiadrigen Leitung gibt es bei Wechselstrom kapazitive und induktive Effekte.
kapazitiv: Die Drähte wirken wie ein Kondensator, in dessen Zwischenraum ein Verschiebungsstrom fließt.
induktiv: Die Magnetfelder der Ströme in beiden Drähte beeinflussen sich gegenseitig.
Die Geometrie der Leitung hat somit einen Einfluß auf deren Wechselstromeigenschaft.
Wegen der kapazitiven Effekte fließt ein Teil des eingespeisten Stromes nicht bis zum Ende der Leitung, der andere geht schon vorher durch den Kondensatoreffekt verloren.
Wegen der induktiven Effekte verringert sich die Spannung zwischen den Drähten ständig auf dem Weg bis zum Ende der Leitung.

Unendlich lange Leitung: Welcher Wechselstrom stellt sich ein bei vorgebener Wechselspannung?
Wenn man an einer beliebigen Stelle der Leitung Strom und Spannung mißt, dann zeigt sich ein konstantes Verhältnis von beiden.
Dieses Verhältnis ist der Wellenwiderstand und beschreibt die Eigenschaft des Mediums.
Obwohl Spannung und Strom wegen der kapazitiven und induktiven Verluste sich entlang der Leitung ständig verringern, bleibt aber deren Verhältnis gleicht.

Da das Ende einer solchen Leitung unendlich weit weg ist, kommen Reflexionen erst nach unendlich langer Zeit an, d.h. nie.
Und deren Intensität wäre unendlich klein.

Abschlußwiderstand
Bei einer kurzen Leitung (praktisches Beispiel: Fernsehkabel von der Sat-Schüssel bis zum Receiver) ist das Ende nicht weit weg und es kann Reflexionen mit nicht vernachlässigbarer Intensität geben.
Abhilfe: Man bringt am Ende beim Empfänger einen ohmschen Widerstand an, bei dem das Verhältnis von Spannung und Strom genau so ist wie bei einer unendlichen Leitung. Dann gibt es keine Reflexionen. Vom Sender aus gesehen verhält sich die kurze Leitung dann so wie eine unendlich lange.
Ein Kabel mit Wellenwiderstand von 75 Ohm benötigt am Ende einen Widerstand von 75 Ohm.

2.4 Wasserwellen in Kanälen unterschiedlicher Breite

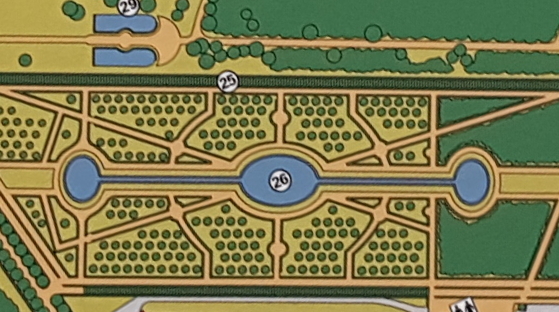Abb. 02-15a: In der Emeritage in Bayreuth gibt es dieses Wasserbauwerk.
Über schmale Kanäle sind drei ovale Becken miteinander verbunden.

Abb. 02-15b: An dem einen Ende läuft ein Springbrunnen. Die Fontaine erzeugt in dem Becken Kreiswellen. (FB)

Abb. 02-16: Kamera um 90° geschwenkt: Die Kreiswellen pflanzen sich auch in dem schmalen Verbindungskanal fort. Dort sind sie am Anfang noch bogenförmig. (FB)

Abb. 02-17: Kamera um insgesamt 180° geschwenkt: Blick auf das mittlere und das hintere Becken. Hinter der Kamera ist das Becken mit der Fontaine. Aus den bogenförmigen Wellen sind parallele Wellen geworden, die nur noch sehr schwach sind. (FB)

2.5 Wellenwiderstand, Nachbildung durch Kapazitäten und Induktivitäten

Abb. 02-18: Nachbildung eines Wellenleiters, der aus Spulen (Induktivitäten) und Kondensatoren zusammengebaut wurde. Diese Anordnung steht stellvertretend für eine lange Leitung aus zwei Drähten. Durch die verschiedenen Steckmöglichkeiten lassen sich Hindernisse (Änderungen des Wellenwiderstandes) einbauen.

Abb. 02-19: Sechs Kondenstoren ändern hier den Wellenwiderstand. (FB)

Abb. 02-20: Spulen: 1 mH, Kondensatoren: 1,95 nF (FB)

2.6 Abschlußwiderstand bei Lecherleitung für Mikrowellen

Abb. 02-21: Zwei parallele Drähte bilden eine Lecherleitung.
Wenn man sie von außen mit Mikrowellen (einige Zentimeter Wellenlänge) bestrahlt, können sich auf dieser Leitung stehende Wellen ausbilden. Die kleine vergoldete Hochfrequenzdiode dient als Detektor, mit dem man Knoten und Bäuche entlang der Leitung nachweisen kann.

Abb. 02-22: Mit einem verschiebbaren Widerstand lassen sich die Eigenschaften der Leitung verändern (FB)

2.7 Wellenwiderstand, Abschlußwiderstand bei einem Koax-Kabel

Abb. 02-23: Praxistaugliches Experiment für den Wellenwiderstand von Koaxialkabeln (Antennleitung für Fernseher)
Der Funktionsgenerator rechts speist mit 1.128 MHz in das Kabel ein. Am linken Ende wird mit dem Oszillographen gemessen. Der obere Meßkanal ist das direkte Signal ( schwarze Verbindung), der untere zeigt das Signal am Ende des Kabels. Damit läßt sich Laufzeit im Koaxialkabel ermitteln: 40 Meter, ein Abschlußwiderstand ist offen (FB)

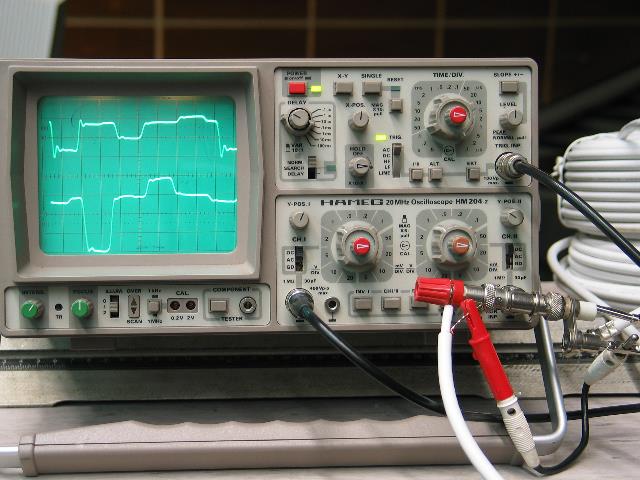Abb. 02-24: Das Kabel ist nicht mit korrekten Widerständen abgeschlossen. Es gibt Reflexionen.
0.1 us/div (FB)

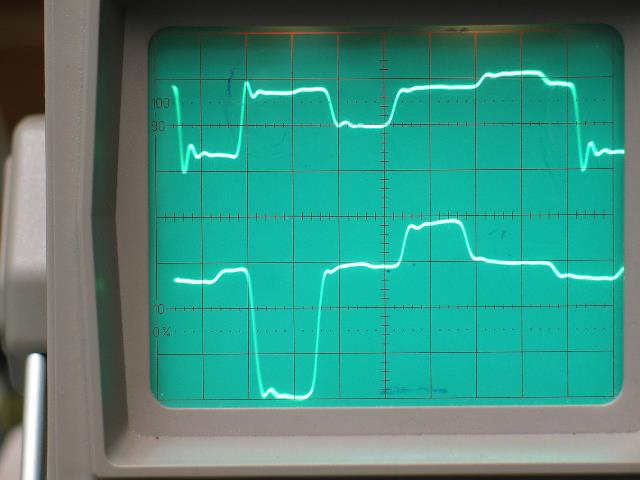Abb. 02-25: Ausschnitt, ohne Abschlußwiderstände gibt es Reflexionen an den Enden. (FB)

Abb. 02-26: Laufzeit im Koaxialkabel 1,5 Einheiten bei 0.1 us/div, also 0.15 us.
bei 40 Meter, v= 40 m / 0.15 us =266 000 000 m/s (etwa 90% der Lichtgeschwindigkeit)

Signal mit Abschlußwiderständen auf beiden Enden, TastPauseVerhältnis ungleich eingestellt (FB)