Beobachtungen:
Blechblasinstrument - Teil 0
Materialsammlung zu
Physik und Technik
der Musikinstrumente und anderen
Schallquellen
+++++++++++++++++++++++++++
Start
A Übersicht
A0 Schall überall
A1 Ergebnisse, Tenorhorn, Frequenzen
A2 Tonhöhen und Klänge
0. Frequenzanalyse als Werkzeug
0.0 Akustische Rohre
0.0.1 Stehende Wellen auf einem Gummiseil - analog zu stehenden Wellen im Rohr
0.0.2 Schwingende Saite
0.0.3 Zahnrad
0.0.4 Akustische Rohre für Musikunterricht
0.0.5 Akustische Rohre für Physik-Anfängerpraktikum, Xylophon
0.0.6 Klarinette
0.0.6a Blockflöte
0.0.6b Querflöte
0.0.7 Stimmung, Dämpfung, Einschwingen
0.0.8 Einschwingvorgang beim Akustischen Rohr
0.1 Zugposaune auf das Mundstück geklatscht
0.2 Zugposaune geblasen, tiefster Ton
1. weitere Instrumente
1.1 Tenorhorn, Anregung mit Klatschen
1.2 Trompete mit Plastikschlauch, Anregung mit Klatschen
2. Form und Frequenzspektrum der Harmonischen
2.1 Tenorhorn geblasen
2.1a Messung vom 17.3.2020
2.1b Wiederholung am 18.03.2020
2.2 Trompete mit Plastikschlauch geblasen
2.3. Tenorhorn, Frequenzdurchlauf (Sweep)
3. Sonstige Blechblasinstrumente
4. Löcher, Klappen und Ventile
4.1 Gutes oder schlechtes Zusammenspiel von Schwingungserzeuger und Resonator
4.2 Helmholtz-Resonatoren
4.3 Frequenz und Wellenlänge bei vier Oktaven, wohltemperierte Stimmung
4.4 Verkürzung des Akustischen Resonators
4.5 Holzblasinstrumente, Aufbau, Mechanik
4.5a Blockflöte
4.5b Querflöte
4.5c Oboe
4.5d Klarinette
4.5e Saxophon
4.5d Fagott
4.6 Verlängerung des akustischen Resonators
5. Historische Meßgeräte zur Akustik
6. zwei- und dreidimensionale Klangerzeuger
6.1 Membranen
6.2 Glocken
6.3 Klangstab
7. Menschliche Stimme
7.1 Obertongesang
++ ++++++++++++++++++++++++++++
0. Frequenzanalyse als Werkzeug
Für die Analyse gibt es unterschiedliche Verfahren, das Instrument anzuregen:
Verfahren-1: man nutzt den Frequenzerzeuger als Anreger d.h. das Instrument wird gespielt,
Verfahren-2: man regt den Hohlraum von außen kurzzeitig mit einem akustischen Impuls (Klatsch, Knall) an.
Verfahren-3: man spielt dem Instrument von außen einen Ton mit gleitender Frequenz (Sweep) vor.
In den Fällen 1 und 2 reicht schon eine kurze Aufzeichnung per Mikrofon im Bereich von Sekunden aus.
Bei 3 dauert die Aufnahme viele Sekunden. Allerdings ist die Auswertung einfacher und schneller.
0.0 Akustische Rohre
Einfache zylindrische Rohre aus Pappe, Kunststoff oder Metall eignen sich hervorragend für Experimente mit stehenden Wellen und Obertönen. Es müssen nicht unbedingt die bunten „musiktauglichen“ sein.
Die Töne lassen sich durch Klopfen oder auch durch einen kleinen Lautsprecher (Ohrhörer) anregen und mit einem Mikrofon an einem Stab im Innenraum abtasten.
Es sind sowohl symmetrische Anordnungen (offen-offen oder geschlossen-geschlossen) als auch unsymmetrische möglich.
Bekannterweise hat eine gedackte Orgelpfeife die halbe Frequenz von der einer offenen.
Wenn es um die exakte Intonation geht, dann spielt der Unterschied zwischen akustischer und geometrischer Länge eine starke Rolle.
0.0.1 Stehende Wellen auf einem Gummiseil - analog zu stehenden Wellen im Rohr
 9,2 Hz |
||||||||||||||||||||||||||
 17,3 Hz |
||||||||||||||||||||||||||
 26,6 Hz |
||||||||||||||||||||||||||
 37,7 Hz
|
||||||||||||||||||||||||||
 45,2 Hz |
||||||||||||||||||||||||||
 53,6 Hz |
||||||||||||||||||||||||||
 72,1 Hz |
||||||||||||||||||||||||||
| Abb. 00-00-01: Stehende Welle auf
einem Gummiseil. Rechts ist ein Motor, der das Seil
zum Schwingen anregt. Nur Wellen, deren Länge ein ganzzahliger
Teil der Länge des Seiles ist, können sich
stabil ausbilden. Bei passender Anregefrequenz
geht das Seil damit in Resonanz. Die
Schwingungsamplitude steigt innerhalb von kurzer
Zeit stark an. Die zugehörigen Frequenzen sind dann jeweils ein Vielfaches von der Grundfrequenz, d.h. bei der Schwingung mit der größten Wellenlänge. Im unteren Bild sind es acht Teile. Über einen Generator (unten in der Mitte), dessen Frequenz sich einstellen läßt, wird der Motor betrieben. stehende-welle.htm (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
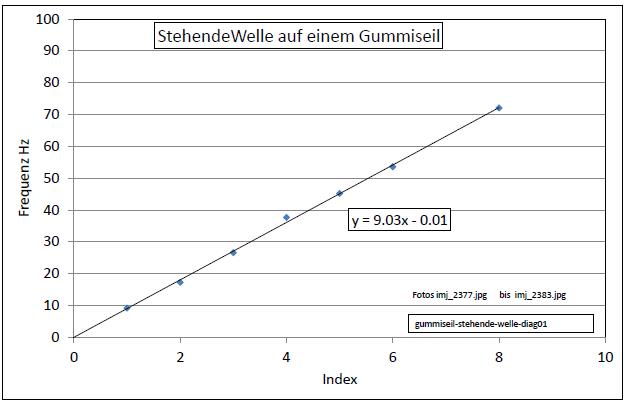
Abb. 00-00-01a: Trägt man die
Resonanzfrequenzen gegen die Anzahl der
Schwingungsbäuche auf, so ergibt sich eine Gerade.
Deren Steigung ist 9,03 Hz. Das ist auch die
Resonanzfrequenz der Grundschwingung.
Der Begriff Harmonische trifft für alle zu. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-01b: Leicht verstimmt,
die Frequenz des Motors ist etwas zu hoch.
Der Knoten verschiebt sich nach links, die Bäuche
verkürzen sich etws, die Wellenlänge ist etwas
kleiner. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-01c: Leicht verstimmt,
die Frequenz des Motors ist etwas zu niedrig,
Der Knoten verschiebt sich nach rechts, die Bäuche
verlängern sich etwas, die Wellenlänge ist etwas
größer. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-02: Stehende Welle in
einem gasgefüllten zylindrischen Rohr. An der Oberkante des Rohres sind kleine Bohrungen, durch die Gas ausströmt. aus wellen.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-02a: Schwingungen auf
einem Draht, zwei ganze Bäuche und ein halber. Die Befestigung des Drahtes ist unsymmetrisch. Es gibt jeweils ein festes und ein loses Ende. Die Anregung erfolgt oben über einen Motor, der periodisch seine Drehrichtung wechselt. aus wellen.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-03: Kunststoffrohre als
Musikinstrument. (Boomwhackers - Tuned Percussion
Tubes) Die beiden äußeren roten Rohre tragen die Bezeichnung "C". Sie haben musikalisch den Abstand einer Oktave (Frequenz 1 : 2), deren Längen sind jedoch im Verhältnis (1 : 2,09) und nicht (1:2) unterschiedlich. Legt man beide Rohre nebeneinander, dann ist das lange Rohr einige Zentimeter länger als zweimal die Länge vom kurzen Rohr. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-04: Verfahren-2 (knallender
Luftballon): Laufzeitmessung in einem "Echo"-Rohr, Bestimmung der Schallgeschwindigkeit Ein rund 10 m langes Kunststoffrohr ist an beiden Enden mit je einem Mikrofon ausgerüstet. Läßt man in einem Ende einen kleinen :Luftballon platzen, so läuft das Geräusch im Rohr mehrmals hin- und her. Bis zu 17 Echos lassen sich innerhalb einer Sekunde verfolgen. Die Schallgeschwindigkeit ergibt sich daraus etwa mit 17 * 2* 10 m/s = 340 m/s. Auswertung: Das Recorder-Programm erlaubt die zeitliche Auslesung der Ereignisse im rechten und linken Mikrofon über ein Fadenkreuz mit der Auflösung des gewählten Meßrasters (max 44 kHz). (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
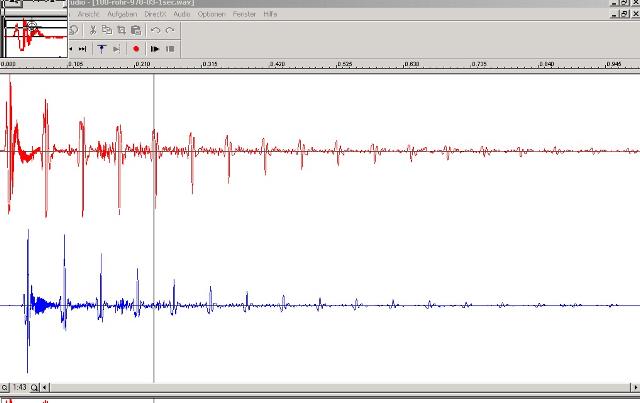
| ABb. 00-00-05: Die beiden
Mikrofonsignale. Jeder blaue Impuls ist auf der
Zeitachse um eine halbe Periode der Impulse bei der
roten Kurve verschoben. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
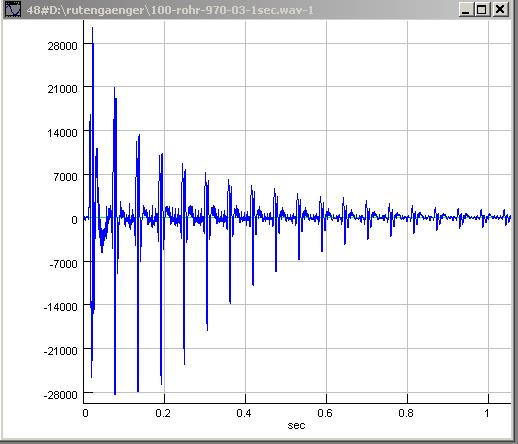
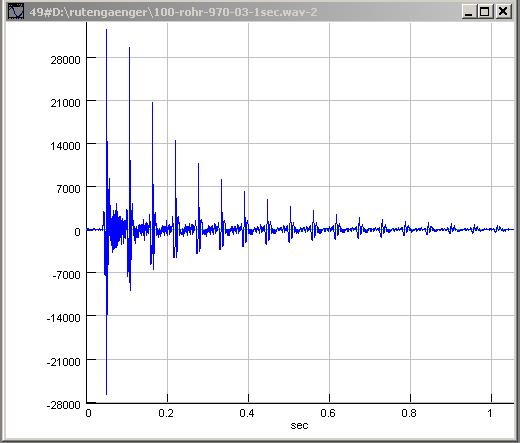
| Abb. 00-00-06: Signal, linkes
Mikrofon 100-rohr-970-03-1sec.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
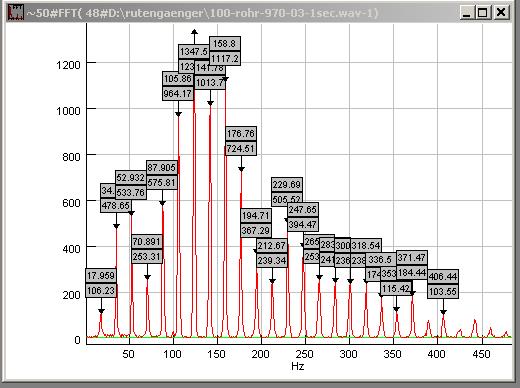
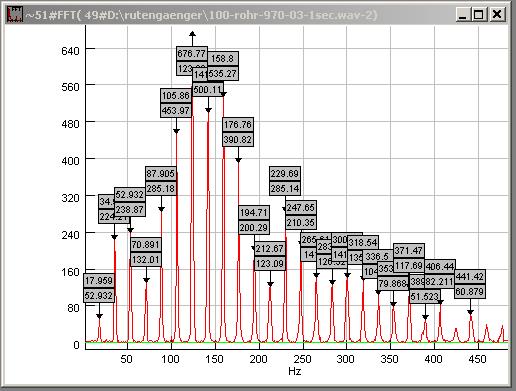
| Abb. 00-00-07: Frequenzanalyse,
linkes Mikrofon 100-rohr-970-03-1sec.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-08: Signal, rechtes
Mikrofon 100-rohr-970-03-1sec.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-09: Frequenzanalyse,
rechtes Mikrofon Die Harmonischen Nr. 6 bis 10 (um 120 Hz herum) haben sehr viel höhere Intensitäten als der Grundton. 100-rohr-970-03-1sec.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
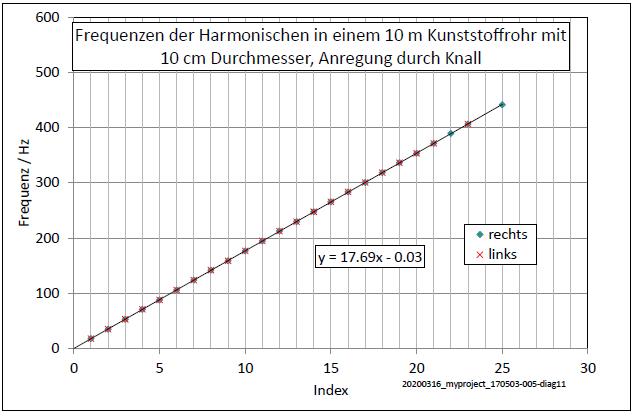
| Abb. 00-00-10: Auswertung der Abb.
00-00-07 und Abb. 00-00-09: Frequenzen der Harmonischen im Kunststoffrohr, angeregt durch einen knallenden Luftballon. Der Abstand der Frequenzen ist 17,69 Hz. Für die Grundfrequenz ergab die Analyse 17,9 Hz. Die exakte Länge des Rohres war 19,4 m, damit ergibt sich mit 17,69 Hz eine Schallgeschwindigkeit von 341 m/s. zum Vergleich Schallgeschwindigkeit in einem Eisenstab: wellen.htm#eisenstab (FB) |
||||||||||||||||||||||||||
0.0.2 Schwingende Saite |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-11: Schwingende Saite, sie
wird elektrisch angeregt und schwingt bei passender
Frequenz sichtbar bzw. auch mit einem kleinen
Papierstück führlbar. Die Harmonischen mit niedrigen Frequenzen lassen sich noch gut mit den Augen verfolgen. (FB) |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| Abb. 00-00-11a: Am linken Rand ist
die Seite in Ruhe, rechts schwingt sie um einige
Millimeter. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-12: Durch die Saite
fließt ein Wechselstrom mit einstellbarer Frequenz.
Der äußere U-förmige Permanentmagnet sorgt dafür,
daß auf die Saite im Takt des Wechselstromes eine
Kraft wirkt - wie bei einem Elektromotor.
Sie gerät dadurch in Schwingungen. (Die Saite zusammen mit dem gelben Papier arbeitet hier wie ein Lautsprecher.) Die Ausschläge sind bei Resonanz so stark, daß man Knoten und Bäuche sogar mit den Augen verfolgen kann. Zusätzlich gibt es einen Schallgeber (gelbes Papier) auf der Saite, und mit dem Mikrofon dahinter lassen sich die Töne aufgezeichnen. Man findet stehende Wellen mit ähnlichem Verhalten wie in den obigen Abbildungen mit dem Gummiseil. Allerdings zeigt eine Saite aus einem einfachen Metalldraht -wie hier- zusätzliche Effekte im oberen Frequenzbereich, die mit der Biegesteifigkeit zusammenhängen: Die Frequenzen der Harmonischen nehmen bei höheren Nummern zu. Die Saite wirkt härter. gekoppelt.htm#monochord Nur bei guten Saiten verhält es sich anders. Dieser Aufbau kann auch in umgekehrter Anordnung wie ein Tonabnehmer wirken - wie bei einem Elektrogenerator und eine Spannung erzeugen. Zupft man die Saite mit der Hand oder streicht sie mit einem Bogen, dann führt die Bewegung in dem Magnetfeld zu induzierten Spannungen, die sich am Ende der Saite abgreifen lassen.. (Funktion eines Mikrofons oder Tonabnehmers) (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
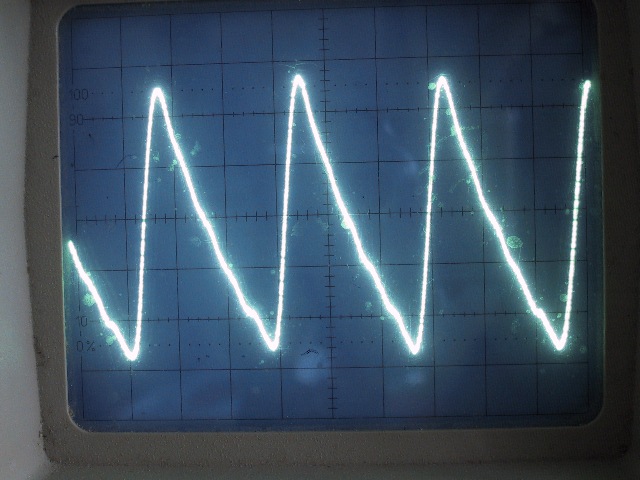
| Abb. 00-00-12a: Eine Saite aus Metall
erzeugt an ihren Enden eine elektrische
Wechselspannung, wenn sie in einem homogenen
Magnetfeld schwingt. Streicht man die Saite mit einem Bogen, dann bekommt man die Form eines Sägezahns mit sehr vielen starken Obertönen. Zupft man sie, erhält man eine Sinusschwingung mit wenigen Obertönen. aus oberton-saite.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
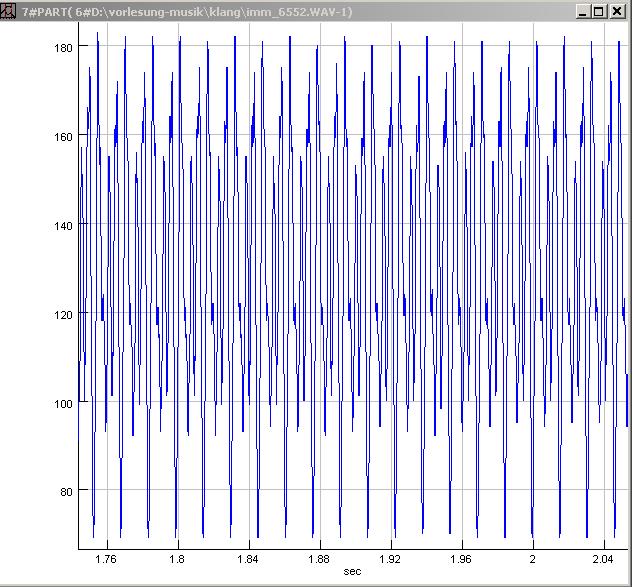
| Abb. 00-00-12b: Eine andere
Aufnahme: Die Schwingungform ist nicht
sinusförmig. imm_6552.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
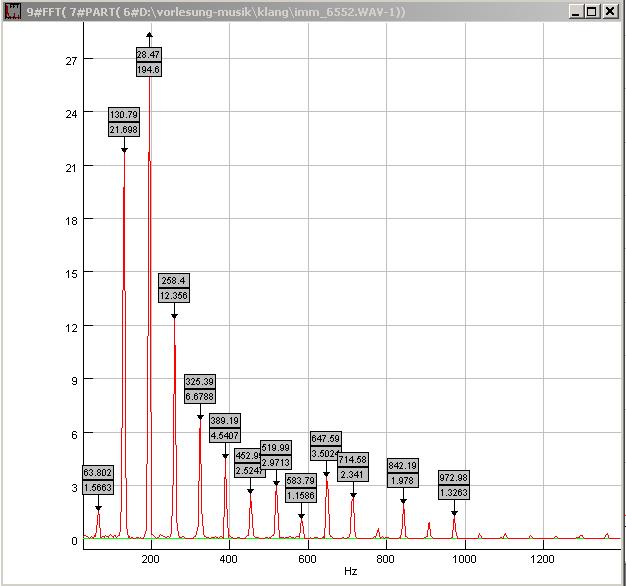
| Abb. 00-00-12c: entsprechend gibt es
viele Harmonische, von denen Nr. 2 bis 5 sehr
intensiv sind. imm_6552.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
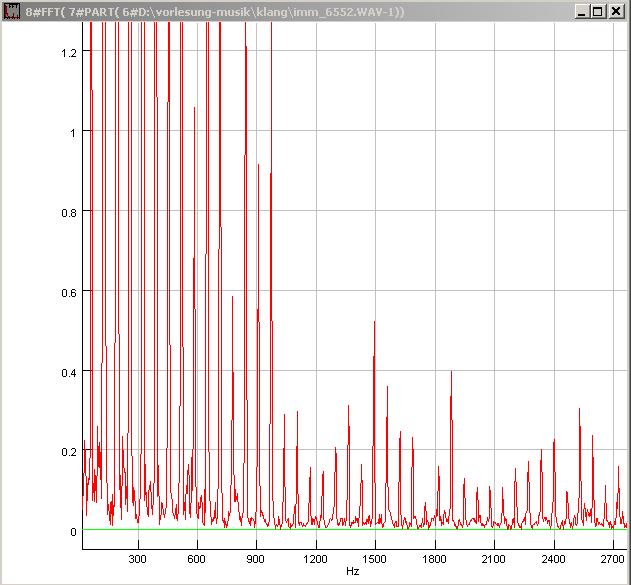
| Abb. 00-00-12d: Sie reichen bis über
3200 Hz hinaus ( Nr. 50). imm_6552.wav
(FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
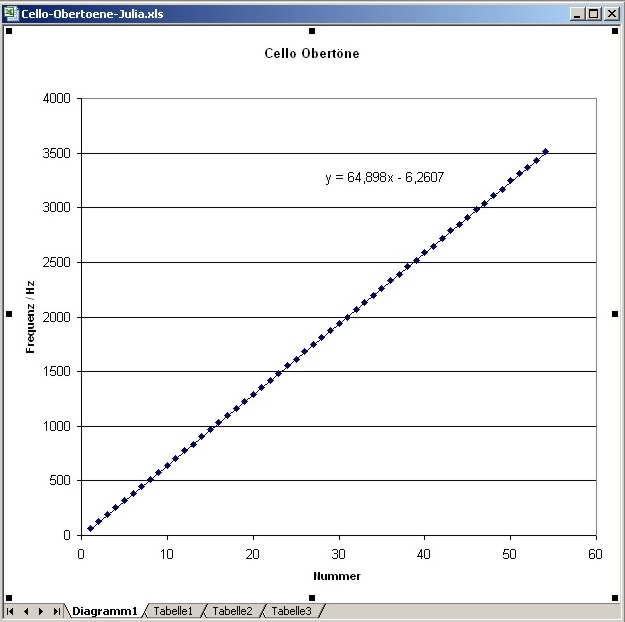
Abb. 00-00-12e: Die Harmonischen von
einer Cello-Saite, auch die schwachen wurden
gefunden. sie reichen bis über 3200 Hz (50.
Harmonische) hinaus.aus oberton-saite.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
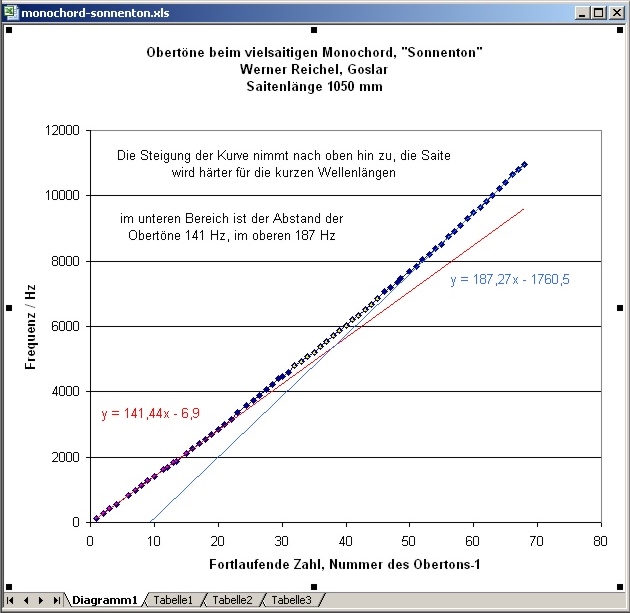
| Abb. 00-00-12f: Die Obertöne eines
steifen Drahtes haben keinen konstanten
Frequenzabstand. Bei hohen Frequenzen, d.h. kurzen Wellenlängen macht sich die Biegesteifigkeit bemerkbar. Die unteren Harmononischen haben einen Frequenzabstand von 141 Hz, die oberen von 187 Hz. Bei einer Saitenlänge von z.B. 105 cm gehört zur 57. Harmonischen eine Wellenlänge von ca. 2 cm. aus gekoppelt.htm#monochord |
||||||||||||||||||||||||||
0.0.3 Zahnrad |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-14: Zahnrad mit 50
Zähnen, zusammen mit einer Plastikkarte kann
es als Frequenzgenerator mit sehr vielen Obertönen
wirken, wenn man es z.B. mit einem
Akkuschrauber antreibt. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-14a: Frequenzanalyse:
Nicht nur das Verschmelzen einzelner Ereignisse zu
einem Ton läßt sich mit Zahnrad und Pappkarte
zeigen, sondern auch das Auftreten von Obertönen,
die einen charakteristischen Klang erzeugen. Für den
Physiker wird sofort das gesamte Obertonspektrum
sichtbar, wenn er das Rad mit einer Bohrmaschine
antreibt und die Klänge analysiert. zahnrad-01.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
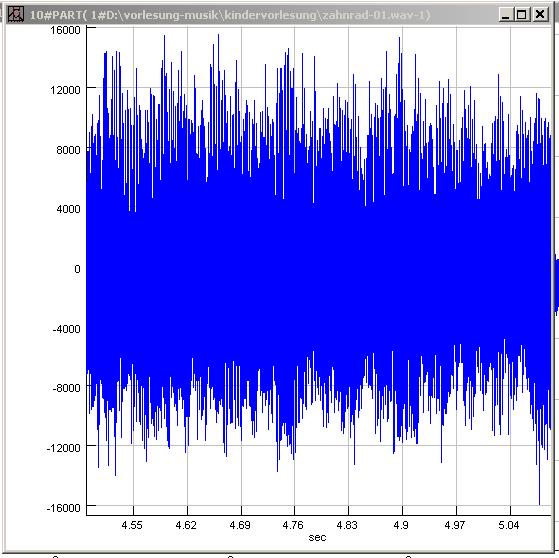
| Abb. 00-00-15: Ausschnitt,
Mikrofonsignal bei 4.5 s. zahnrad-01.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
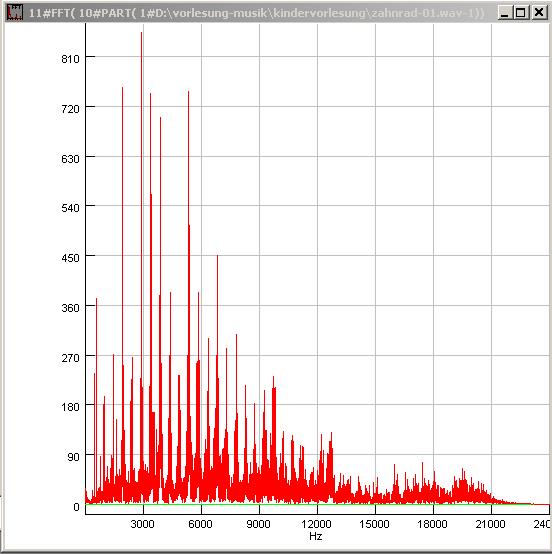
| Abb. 00-00-16: Frequenzanalyse
bei 4,5 s. zahnrad-01.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-17: Harmonische der
Frequenzanaylse vom Zahnrad bei 4,5 s. Der Frequenzabstand beträgt 485 Hz. Die Grundfrequenz lag auch etwa in diesem Bereich. Bei 50 Zähnen pro Umdrehung ist der Motor mit 485/50 also knapp 10 Umdrehungen pro Sekunde gelaufen. zahnrad-01.wav (FB) |
||||||||||||||||||||||||||
0.0.4 Akustische Rohre für Musikunterricht |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
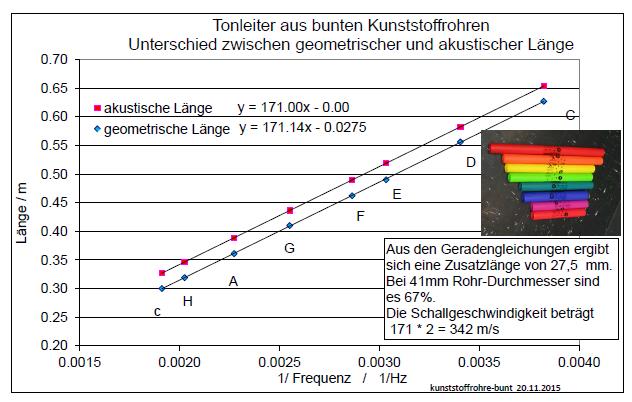
| Abb. 00-00-18: Akustische Rohre als
Musikinstrumente. Sie sind im Musikgeschäft
erhältlich. (Boomwhackers) Zur
Tonerzeugung hält man das Rohr in der Hand und
schlägt von der Seite auf das Rohr auf das andere
Ende. Diagramm: Einfluß der Rohrenden auf den Zusammenhang zwischen Länge und Resonanzfrequenz: Trägt man die geometrische Länge gegen die reziproke Frequenz auf, so ergibt sich eine Gerade (blau), die zu der rechnerisch erwarteten (rot) um etwas nach unten verschoben ist. Der Unterschied ist 2,7 cm, das sind 2/3 des Durchmessers. Daraus folgt, dass die Knoten am Rohrende etwas ausserhalb liegen. Aus der Steigung folgt die Schallgeschwindigkeit mit 342 m/s. kunststoffrohre-bunt.xls (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-18a: Die schwarzen Deckel
sind passend für die Rohre gefertigt. Damit lassen
sich die Rohrenden verschließen ("gedackte" Rohre).
Wenn die Frequenz passend zu der Stimmung der offenen sein soll, dann muß der Abschluß etwas außerhalb vom Rohrende sein. (1/3 vom Rohrdurchmesser) (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-18b: Bis zur Verdickung
lassen sich die Deckel aufschieben. Es bleibt etwa
ein Drittel des Durchmessers. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-18c: Messung der
Harmonischen vom langen C-Rohr, links ein Ohrhörer als Schallgeber, rechts ein Mikrofon (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
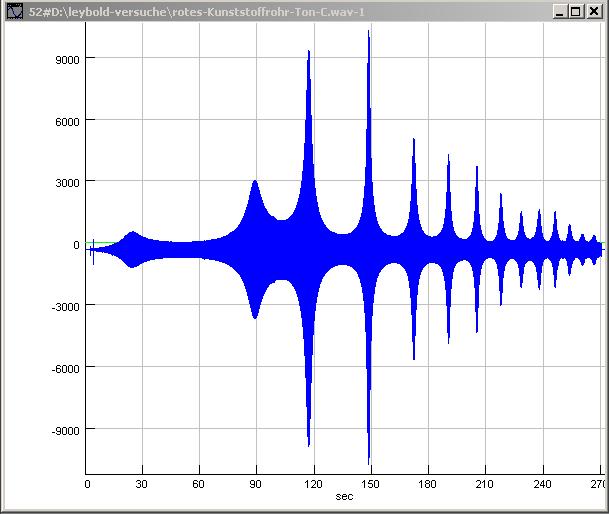
| Abb. 00-00-19: Verfahren-3:
Mikrofonsignal bei dem langen roten Kunststoffrohr
(Ton C) wenn ein kleiner Ohrhörer einen Ton in das
Rohr eingespeist und dabei die Frequenz in einer
Rampe ansteigt. Es ist deutlich zu sehen, wie die Intensität bei einigen Harmonischen stark und bei anderen schwach ist. x-Achse: Zeit / s rotes-kunststofffohr-ton-c.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
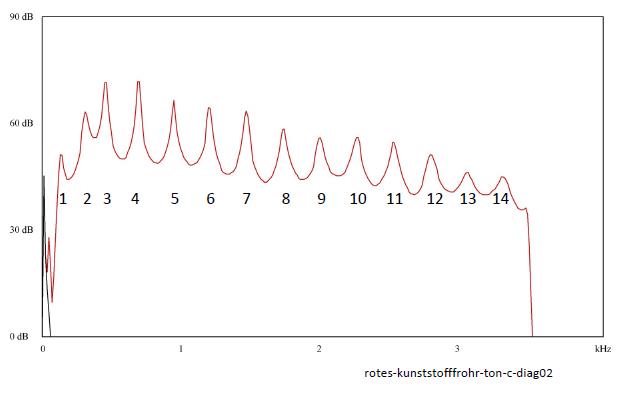
| Abb. 00-00-20: Verfahren-3: Impedanz
bei dem roten Kunststoffrohr (Ton C). Man sieht die Aufeinanderfolge der Obertöne Man läßt das Programm die Frequenzanalyse durchführen und dabei in einer zweiten Kurve die Maximalwerte des Mikrofonsignals speichern. (R. Horne, Spectrogram) http://fledermaus.wtal.de/spectro1.htm http://www.visualizationsoftware.com/ local unter http://db0fhn.efi.fh-nuernberg.de/~dg8ygz/voicetools/ x-Achse: Frequenz / Hz rotes-kunststofffohr-ton-c.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
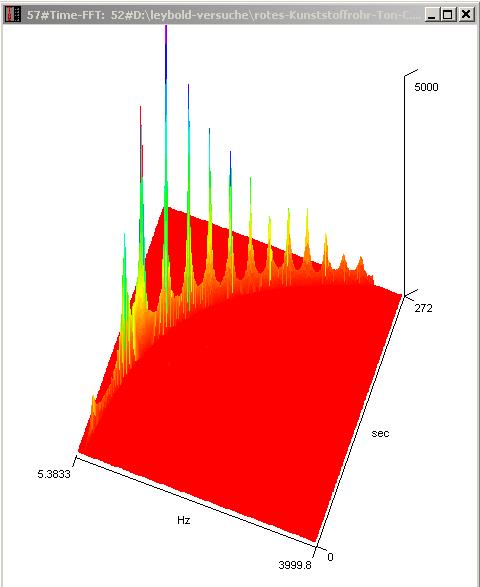
| Abb. 00-00-21: Impedanz bei einem
bunten Kunststoffrohr. Die Frequenzachse geht von ca. 5 Hz bis 4000 Hz, die Zeitachse von 0 bis 272 s Die Tonhöhe steigt mit einem konstanten Faktor pro jeweiligen Zeitabschnitt, d.h. nicht linear mit der Zeit an. Diagramm SigView32 rotes-kunststofffohr-ton-c.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
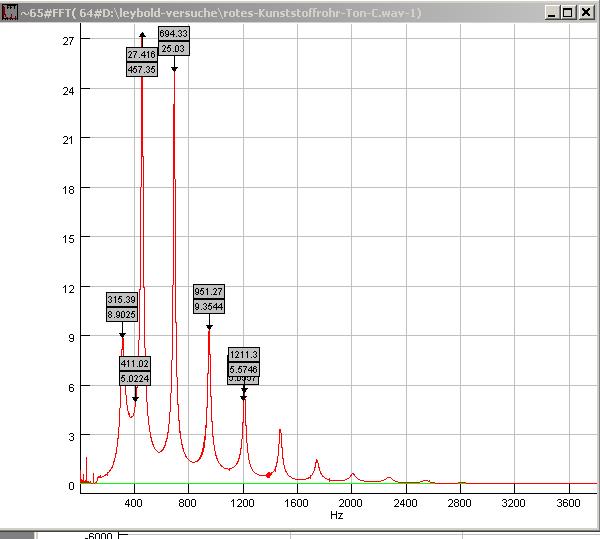
| Abb. 00-00-21a: mit SigView32
analysiert. Mindestens 12 Harmonische sind zu
erkennen. rotes-kunststofffohr-ton-c.wav (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
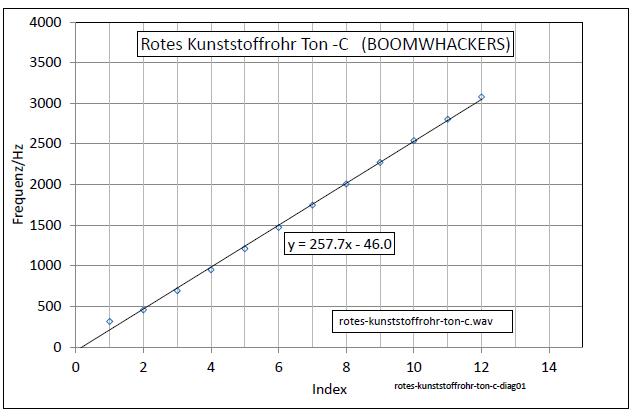
| Abb. 00-00-21b: Die Frequenzen der
Peaks aus der Abbildung vorher. Die Steigung der Geraden gibt den Frequenzabstand der Harmonischen mit 257,7 Hz an. Die unterste Harmonische weicht mit 315 Hz etwas davon ab. Der Höreindruck ergibt sich aber für den Ton C4 (bei wohltemperierter Stimmung (440Hz) wären es 261 Hz, )
|
||||||||||||||||||||||||||
0.0.5 Akustische Rohre für Physik-Anfängerpraktikum, Xylophon |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-22: Verfahren 3:
Kunststoffrohre im Anfängerpraktikum. Eingekoppelt
wird jeweils von der Seite über einen Ohrhörer. Bäuche und Knoten der stehenden Welle lassen sich innerhalb des Rohres mit einem kleinen Mikrophon an der Stange untersuchen. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-23: baugleich: Ohrhörer
und Mikrophon an einer dünnen Stange (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
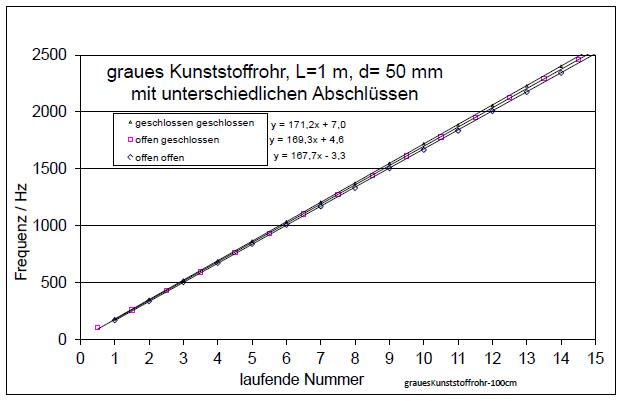
| Abb. 00-00-24: Verfahren 3: Frequenzen der Harmonischen bei unterschiedlichen Abschlüssen an den Enden des 1 m langen Rohres. Auch für diese Sanitärobjekte gilt, dass die Knoten bei offenen Enden etwas außerhalb der Rohre zu finden sind. Für drei Abschluß-Varianten (offen, geschlossen und offen-geschlossen) sind die Frequenzen der Grund- und Obertonreihe aufgetragen. Wie auch die Steigungen (167,7; 169,3 und 171,2 Hz, Grundton) zeigen, hat die Anzahl der offenen Enden einen direkten Einfluß auf die Intonation. Damit die Geraden zusammenpassen, sind bei den beiden symmetrischen Varianten die Töne ganzzahlig und bei der gemischten halbzahlig beziffert. Die Frequenz der letzteren ( der "gedackten" ) ist natürlich etwa die Hälfte von den anderen. (27.2.2005) grauesKunststoffrohr-100cm.xls (FB) |
||||||||||||||||||||||||||
0.0.5a Akustische Rohre bei einem Xylophon |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
Abb. 00-00-24a: Akustische Rohre bei
einem Xylophon
aus xylophon.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
Abb. 00-00-24b: Die Öffnung der
Resonanzrohre befindet sich einige Zentimeter von
den Klangstäben entfernt. Die stehende Welle in den
Rohren reicht bis zu den Hölzern.aus xylophon.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
Abb. 00-00-24c: Die Rohre sind
"gedackt", haben ein geschlossenes Ende.aus xylophon.htm |
||||||||||||||||||||||||||
0.0.6 Klarinette |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-25: A-Klarinette, Länge
69,5 cm, Bohrung 15 mm B-Klarinette, Länge 66,5 cm, Bohrung 15 mm 69.5/66.5 = 1.045, einem Halbton entspräche 1.059 (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
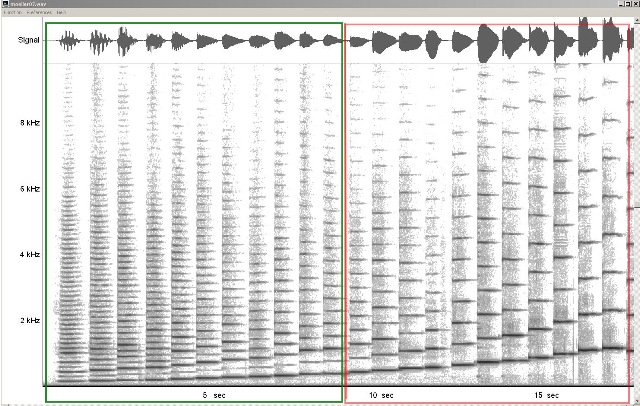
| Abb. 00-00-25a: Tonleiter
aufwärts, Frequenzanalyse, lineare Skala gespielt auf einer A-Klarinette mit Messingklappen, Buchsbaum 1810, Abbildung Tonaufnahme freundlicherweise zur Verfügung gestellt von Norbert Möller, Berlin unterschiedliche Lagen des Instrumentes, Bezeichnung der Töne wie notiert, nicht wie klingend. tiefe Lage (grün) zweite Lage (Überblasen) (rot) F3, G3, A3, B3, C4, D4, E4, F4, G4, A4, B4, C5, D5, E5, F5, G5, A5, B5, C6, D6, E6, F6 Daten aus frequenz-analyse.htm |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-26: Der zweit tiefste Ton
der A-Klarinette, notiert F3,
klingend D3 (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
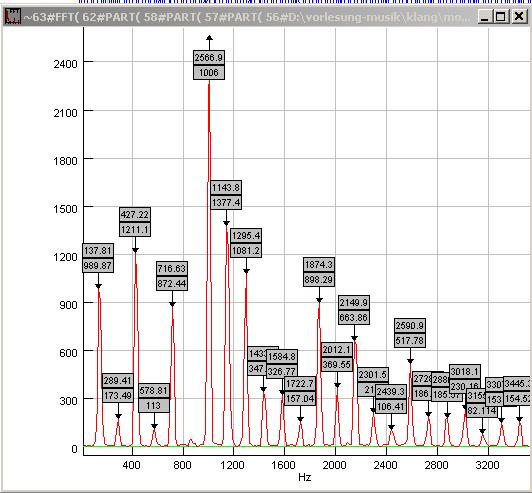
| Abb. 00-00-27: Frequenzanalyse vom
Ton F3. Die ungeraden Harmonischen sind im
unteren Bereich schwach. Beim Überblasen kann daher
keine Oktave erklingen, sondern es kommt die
dritte Harmonische im Abstand einer Duodezime
C4. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
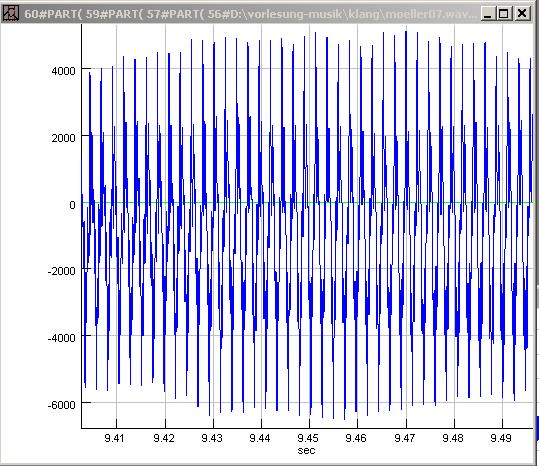
| Abb. 00-00-28: Überblasen: Der erste
Ton in der zweiten Lage. notiert C5,
klingend A4 (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-29: Frequenzanalyse, C5,
auch hier ist die zweite Harmonische schwächer als
die benachbarten. (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
| Abb. 00-00-30: A-Klarinette
Buchsbaum von 1810, Frequenzen der Harmonischen
vom tiefsten Ton F3 und ersten überblasenen Ton C5 (Bezeichnung der Griffe, nicht wie klingend) gegriffen: F3 alle Finger bis auf kleinen Finger der linken Hand, C5 genauso, aber linker Daumen abgehoben ("Oktavöffnung") Frequenzabstand der beiden Harmonischen 426.8 Hz und 142.2 Hz. 426.8 / 3 = 142.20 ( Duodezime Frequenzverhältnis 3:1 ) Abbildung (FB) |
||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||
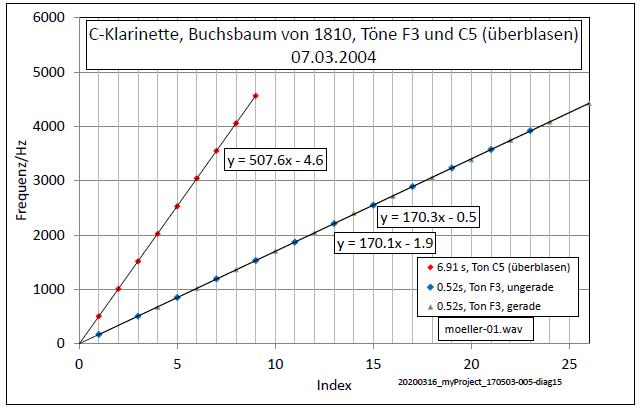
| Abb. 00-00-31: baugleich, passend zur
A-Klarinette: C-Klarinette Buchsbaum von 1810, Frequenzen der Harmonischen vom tiefsten Ton F3 und ersten überblasenen Ton C5 (Bezeichnung der Griffe und auch wie klingend, da C-Instrument) Frequenzabstand der beiden Harmonischen 507.6 Hz und 170.3 Hz. 510 / 3 = 170 ( Duodezime Frequenzverhältnis 3:1 ) Abbildung (FB) |
B-Klarinette, 1962 F.A. Uebel, Markneukirchen
A-Klarinette, 1978 F.A. Uebel, Markneukirchen DDR
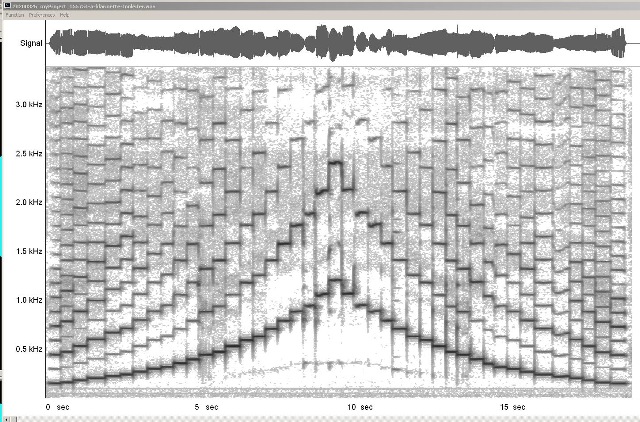 |
| Abb. 00-00-31a: A-Klarinette
1978, lineare Frequenzachse Tonleiter von E3 (gegriffen) bis F6 (gegriffen) klingend #C3 140 Hz und D6 1208 Hz 20200326_myProject_155754-a-klarinette-tonleiter.wav (FB) |
 |
| Abb. 00-00-31b: A-Klarinette 1978
C-Dur Akkorde (gegriffen), klingend #C3, E3,
A3 ... A6 E3 G3 C4 E4 G4 C5 E5 G5 C6 E6 G6 C7 20200326_myProject_160306.wav ab 44 s (FB) |
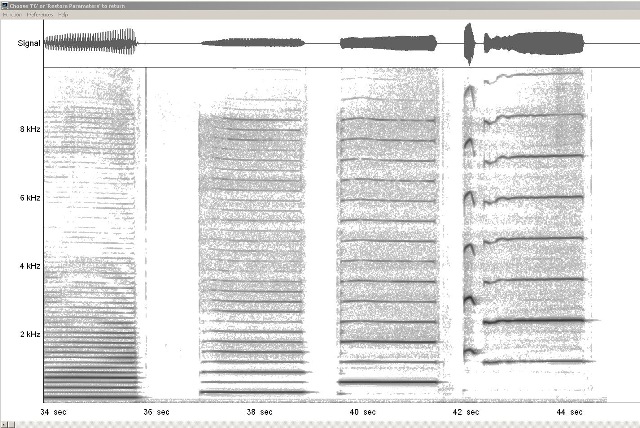 |
| Abb. 00-00-31c: B-Klarinette 1962, Oktaven
von klingend D3 bis D6 Es gibt starke und schwache Harmonische Im unteren Bereich haben die starken Harmonischen ungerade Nummern (Index) Dazwischen gibt es auch schwache mit gerader Nummer. Da die Klarinette an dem einen Ende einen Schwingungsknoten und an dem anderen einen Schwingungsbauch haben soll, dürften in der unteren Lage nur die ungeraden Harmonischen auftreten. Aber auch die anderen sind vorhanden, wenn auch schwach. 20200326_myProject_155925.wav |
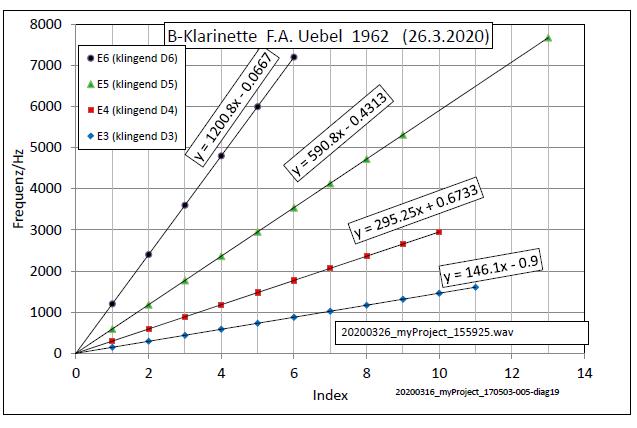 |
| Abb. 00-00-31d: B-Klarinette 1962,
Oktaven von klingend D3 bis D6 starke und auch schwache Harmonische Die Steigungen der Geraden ergeben bei dieser Art der Indizierung (d.h. auch mit den Schwachen) die Frequenzen 146 Hz, 295 Hz , 591 Hz und 1201 Hz (gespielt und gleichzeitig analysiert ergeben sich übereinstimmende Werte bis auf den letzten 1185 Hz) 20200326_myProject_155925.wav (FB) |
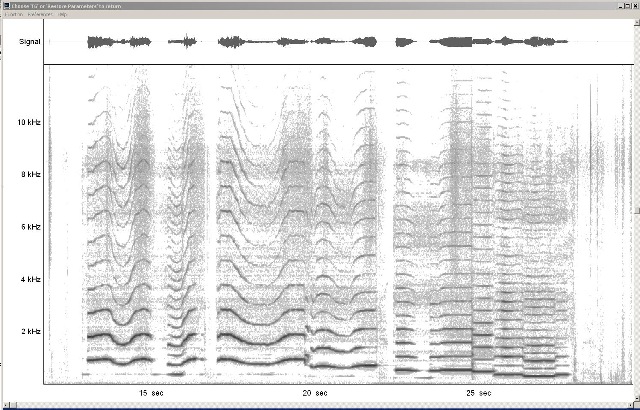 |
| Abb. 00-00-31e: Etwa ab Mitte der
mittleren Lage lassen sich die Tonhöhen durch
Nachlassen der Lippenspannung um mehrere Halbtöne
nach unten ziehen. (Glissando) Beispiel für klingend F5 (689 Hz) Damit lassen sich sprachähnliche Klänge erzeugen. (FB) |
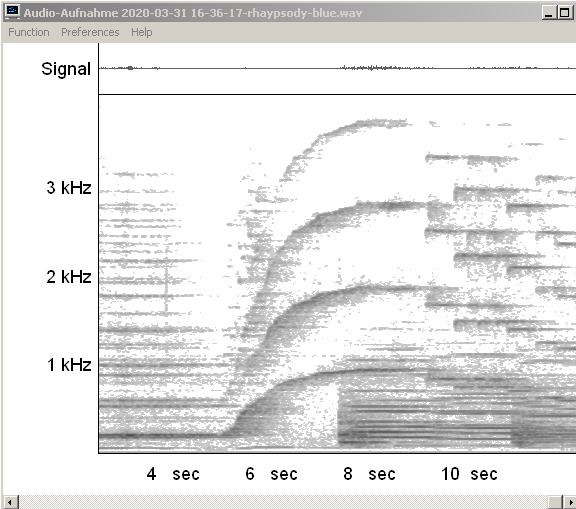 |
| Abb. 00-00-31f: Glissando bei
der Klarinette, nahezu stufenlos über drei Oktaven.
Die ersten Takte von der Rhapsody in Blue, George Gerschwin. |
0.0.6a Blockflöte
 |
| Abb. 00-00-40: Sopran Blockflöte aus
Ebenholz, Länge 31,8 cm (FB) |
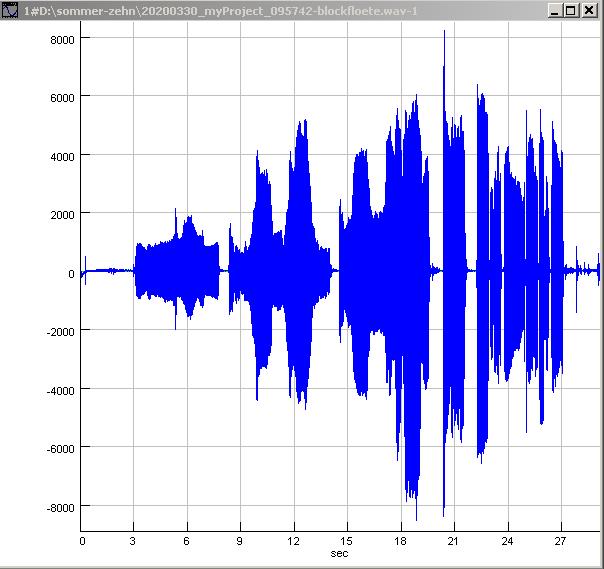 |
| Abb. 00-00-41:mehrere Töne, durch
erhöhte Luftmenge (bei gleicher Griffweise) kommt es
bei langen Tönen sehr leicht zum Überblasen, bei
kürzeren weniger. 20200330_myProject_095742-blockfloete.wav (FB) |
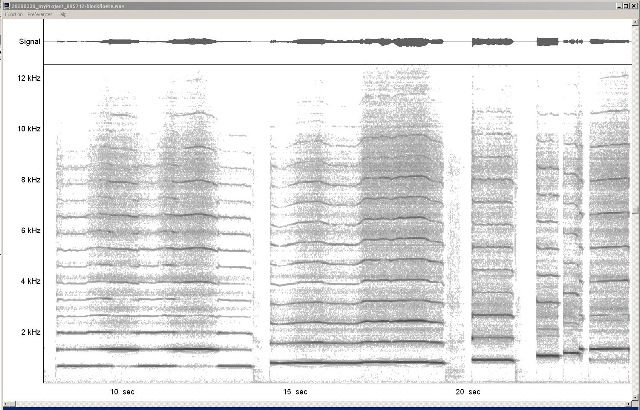 |
| Abb. 00-00-42: Überblasen bei
gleicher Fingerstellung Bereich 8 bis 14 Sekunden: E5 660 Hz normal, kräftig, normal, kräftig normal geblasen Die zweite Harmonische wird kräftiger, die erste schwächer. Insgesamt steigt die Frequenz ( besser sichtbar bei den höheren Harmonischen) Bereich 15 s bis 19 s G5 780 Hz normal, kräftig, normal, kräftig normal geblasen bis auf eine Frequenzerhöhung ändert sich kaum etwas. ab 20s A5, C6 D6 "Lange"* Töne überblasen schon bei geringerem Luftstrom als "kurze" *d.h. mit einigen Fingern der rechten Hand Die Tonhöhe (Stimmung) läßt sich durch die Blastechnik verändern 20200330_myProject_095742-blockfloete.wav (FB) |
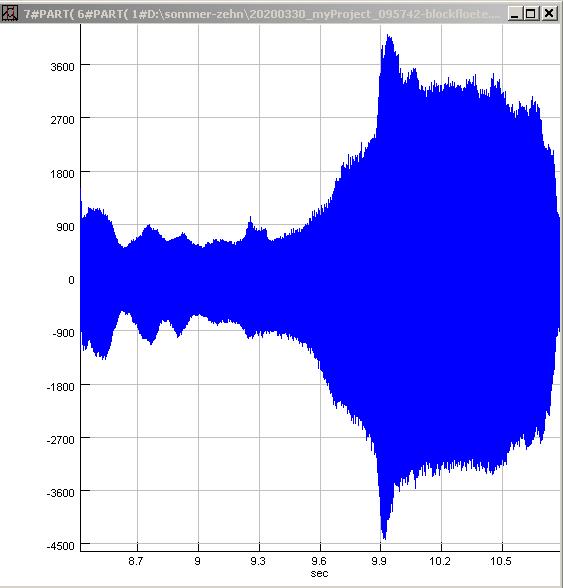 |
| Abb. 00-00-43: E5
660 Hz, normal und zu kräftig geblasen Zwei Tonlöcher für die rechte Hand sind geschlossen. 20200330_myProject_095742-blockfloete.wav (FB) |
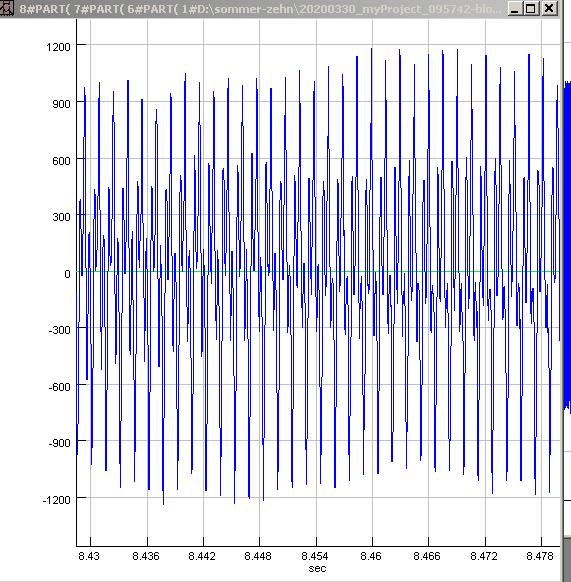 |
| Abb. 00-00-44: E5 650 Hz
normal geblasen 20200330_myProject_095742-blockfloete.wav
(FB) |
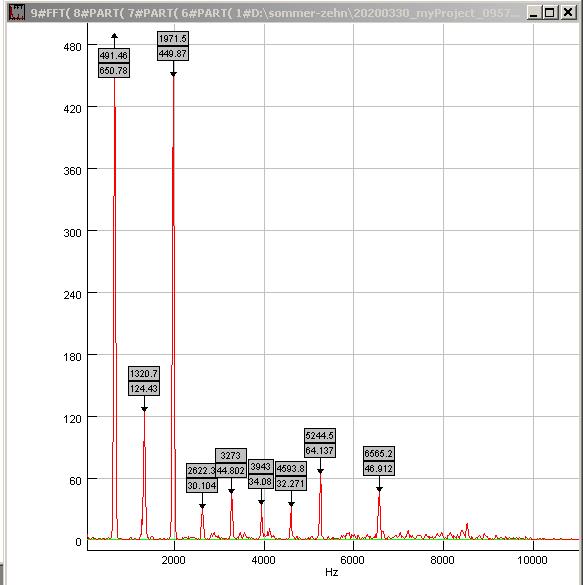 |
| Abb. 00-00-45: normal geblasen E5
650 Hz, die dritte Harmonische ist kräftig 1971
Hz (FB) |
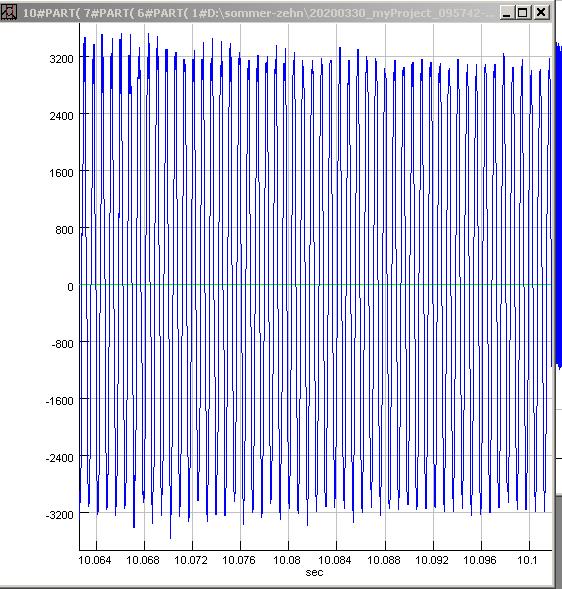 |
| Abb. 00-00-46: E5
kräftig geblasen, doppelte Frequenz 20200330_myProject_095742-blockfloete.wav
(FB) |
 |
| Abb. 00-00-47: kräftig geblasen E5
1323 Hz, Doppelte von 650 Hz (FB) |
Kurzer Ton: Kein Überblasen bei gleicher Fingerstellung, nur bei besonders starkem Blasen
 |
| Abb. 00-00-48: Die Löcher für die
rechten Hand sind offen. G5 normal geblasen 778 Hz 20200330_myProject_095742-blockfloete.wav (FB) |
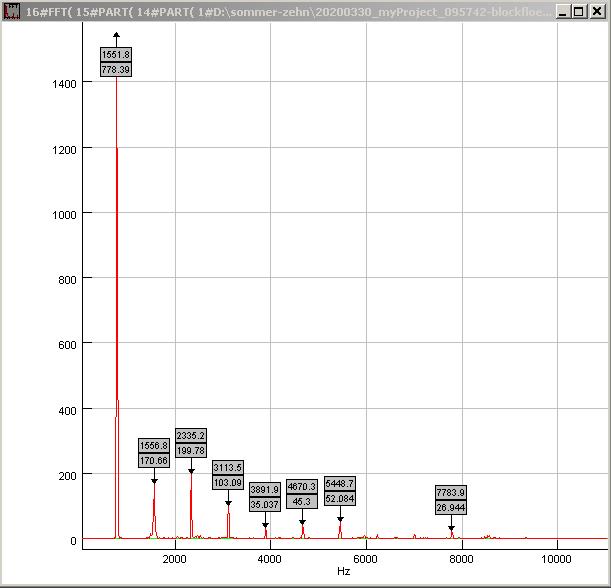 |
| Abb. 00-00-49: G5 normal
geblasen 778 Hz (FB) |
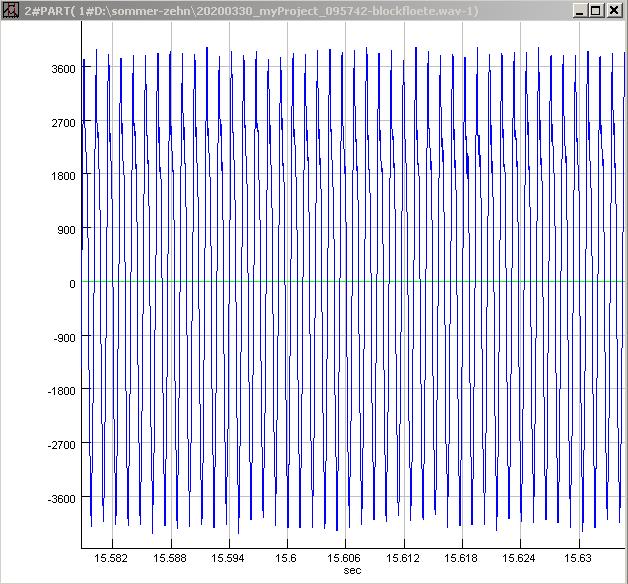 |
| Abb. 00-00-50: G5 kräftig geblasen 793 Hz (erhöht) (FB) |
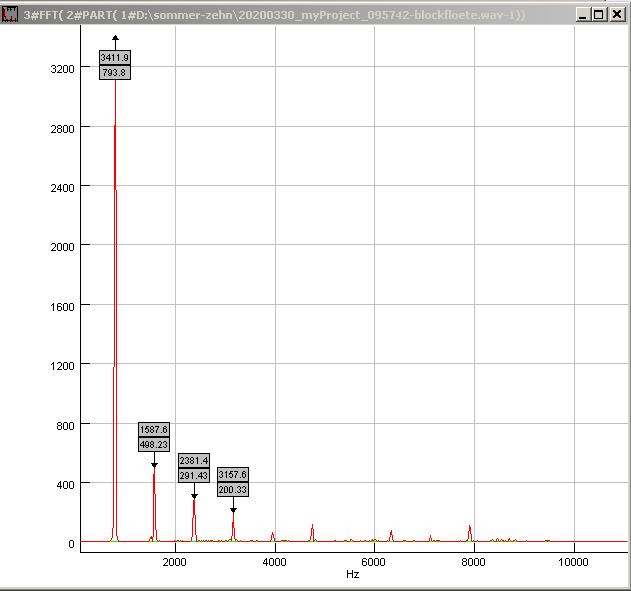 |
| Abb. 00-00-51: G5 kräftig geblasen, 793 Hz (erhöht) (FB) |
0.0.6b Querflöte
 |
| Abb. 00-00-61: Querflöte, Länge 67
cm, Bohrung oben und unten 19 mm (FB) |
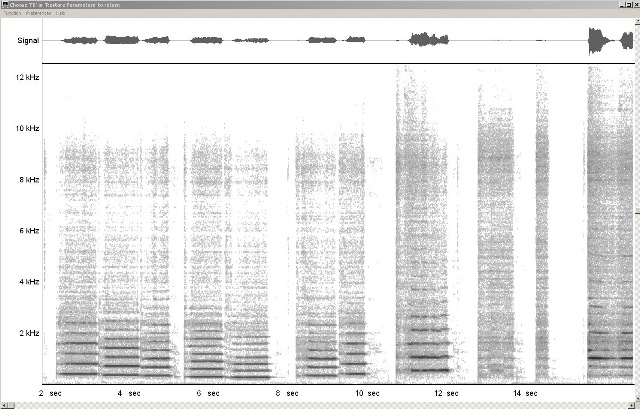 |
| Abb. 00-00-62: Querflöte in der
unteren Lage, nur der letzte Ton ist überblasen. 20200330_myProject_095946-querfloete.wav (FB) |
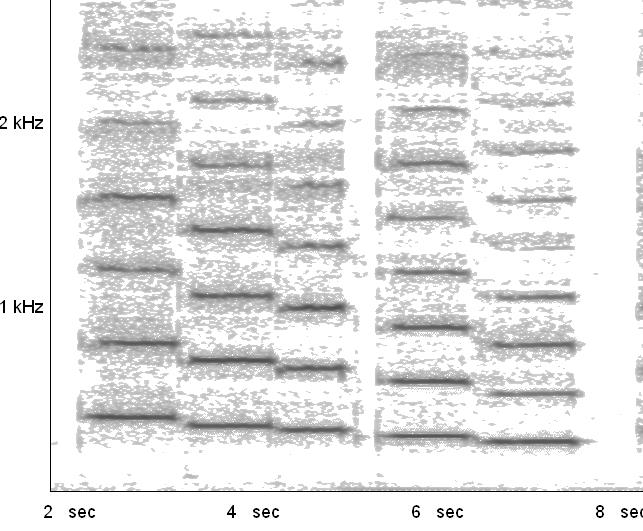 |
| Abb. 00-00-63:
G4
F4
E4
D4
C4 Die ersten drei Harmonischen unterscheiden sich kaum in der Intensität. Sie sind alle stark vertreten. 20200330_myProject_095946-querfloete.wav (FB) |
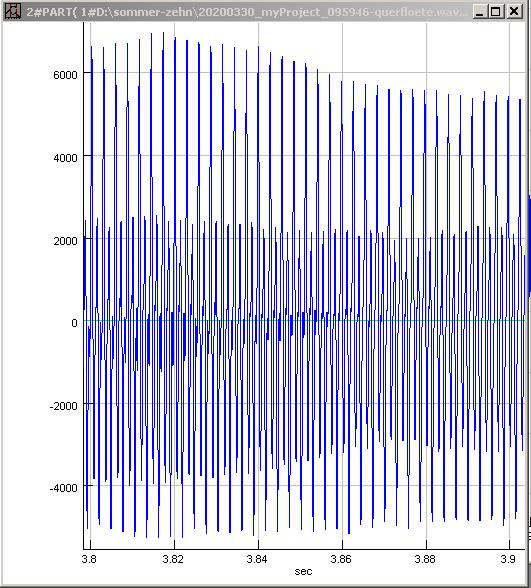 |
| Abb. 00-00-64: F4
349 Hz mehrere Obertöne 20200330_myProject_095946-querfloete.wav
(FB) |
 |
| Abb. 00-00-65: F4
349 Hz mehrere Obertöne, die zweite
Harmonische mit 707 Hz ist am
stärksten. (FB) |
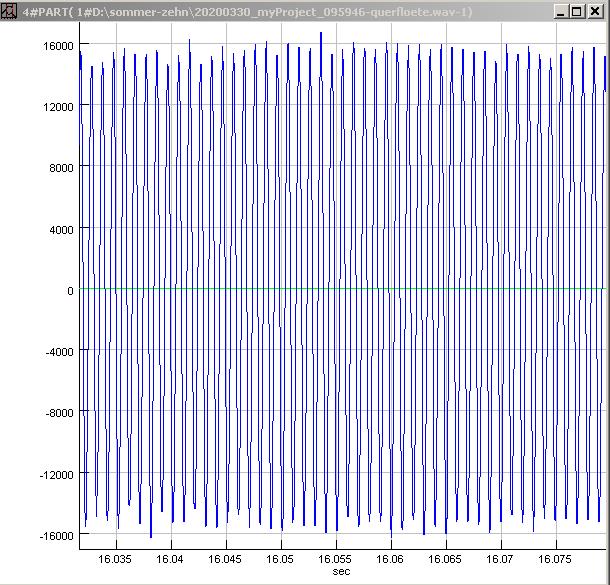 |
| Abb. 00-00-66:
C6 1000 Hz überblasen, sehr
rein, wenige Harmonische 20200330_myProject_095946-querfloete.wav (FB) |
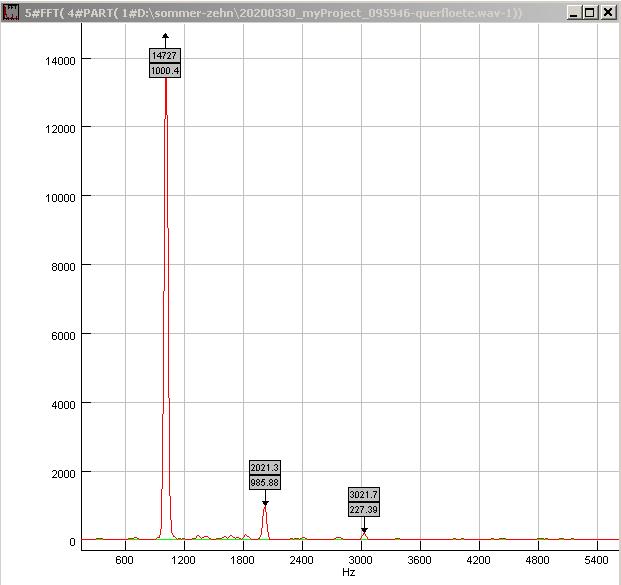 |
| Abb. 00-00-67: C6
1000 Hz, überblasen, sehr rein, es gibt nur
wenige Harmonische (FB) |
0.0.7 Stimmung, Dämpfung, Einschwingen
An einem Pohl'schen Rad, einem Drehpendel im Praktikum lassen sich Schwingungsversuche sehr anschaulich untersuchen, da die Bewegung bei niedrigen Frequenzen so langsam erfolgt, daß man alles gut mit den Augen verfolgen kann.
Das vom Autor für das Praktikum neu entwickelte Clausthaler-Drehpendel arbeitet bei deutlich höherer Frequenz.
So läßt sich Meßzeit einsparen, wenn man z.B. langwierige Einschwing- und Abklingvorgänge untersuchen möchte.
Für die Darstellung braucht es aber eine elektronische Auslesung und ein Computerprogramm, Dinge die mittlerweile leicht zu beschaffen sind. didaktik/honnef_balck02a.pdf
aus quarzrohr-angeregt.htm#kapitel-02-01-01c-5
 |
| Abb. 00-00-33:
Resonanzkurven, Über der Anregefrequenz ist die Amplitude der Schwingung aufgetragen bei unterschiedlichen Einstellungen für die Dämpfung durch eine Wirbelstrombremse (Abstand des Bremsmagneten zur bewegten Aluminuium-Scheibe). Schon in der Nähe der Resonanzfrequenz von 3,5 Hz schwingt das System, allerdings schwächer. Bei geringer Dämpfung ist die Amplitude sehr groß, bei starker Dämpfung klein. Bei der Resonanzfrequenz von 3,5 Hz und verschwindender Dämpfung würde die Amplitude bei jedem Hub der Anregung anwachsen und im Laufe der Zeit beliebig große Werte annehmen, die bis zur Zerstörung des Gerätes führen würden. Übertragen auf ein Blechblasinstrument: Eine Dämpfung ist immer vorhanden, da über den Schall Energie abgestrahlt wird.
|
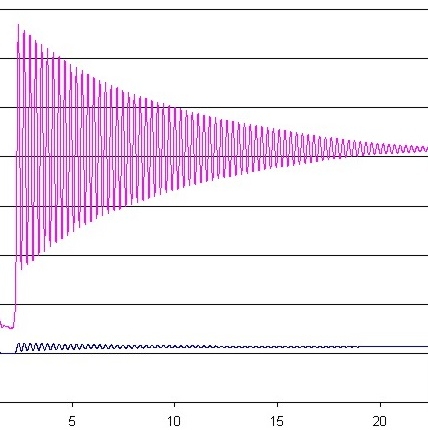 |
Abb. 00-00-34: Abklingen bei
schwacher Dämpfung, Zeit in Sekundenaus gedaempft.htm |
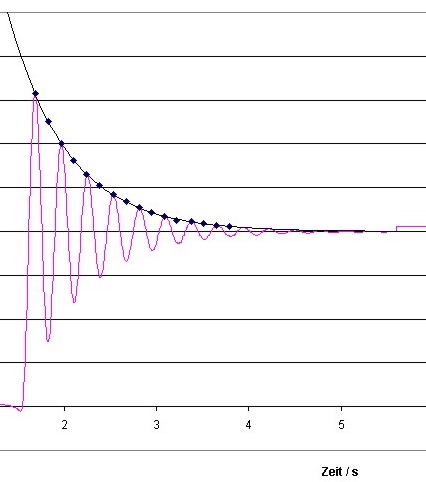 |
Abb. 00-00-35: Abklingen bei
stärkerer Dämpfungaus gedaempft.htm |
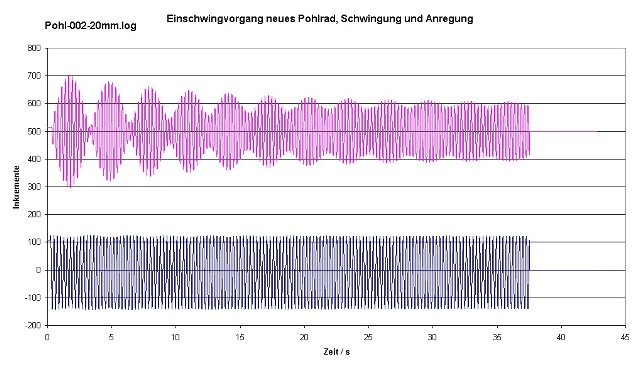 |
| Abb. 00-00-36: schwarz:
Anregung, rot: Antwort des Drehpendels bei schwacher
Dämpfung Die Anregefrequenz ist nicht exakt die Resonanzfrequenz. (FB) |
 |
| Abb. 00-00-30: schwarz:
Anregung, rot: Antwort des Drehpendels bei stärkerer
Dämpfung Die Anregefrequenz ist nicht exakt die Resonanzfrequenz. (FB) |
0.0.8 Einschwingvorgang beim Akustischen Rohr
aus quarzrohr-angeregt.htm#kapitel-02-01-01c-6
 |
Abb. 00-00-37:aus quarzrohr-angeregt.htm#kapitel-02-01-01c-6 |
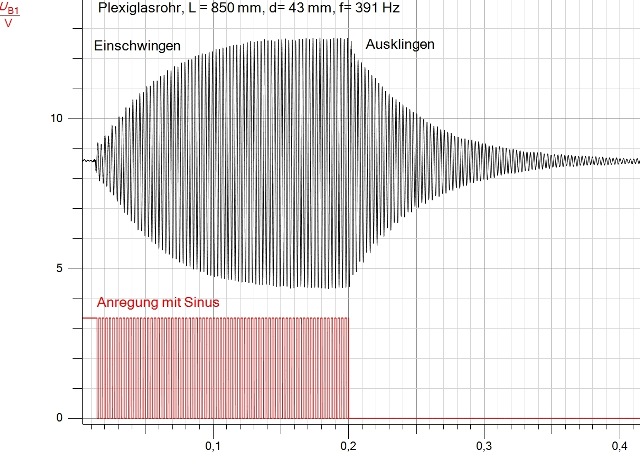 |
Abb. 00-00-38: Einschwingen und
Ausklingen beim akustichen Rohraus quarzrohr-angeregt.htm#kapitel-02-01-01c-6 |
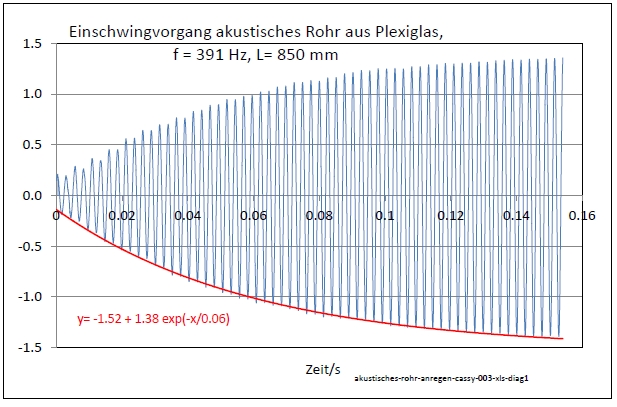 |
Abb. 00-00-39:aus quarzrohr-angeregt.htm#kapitel-02-01-01c-6 |
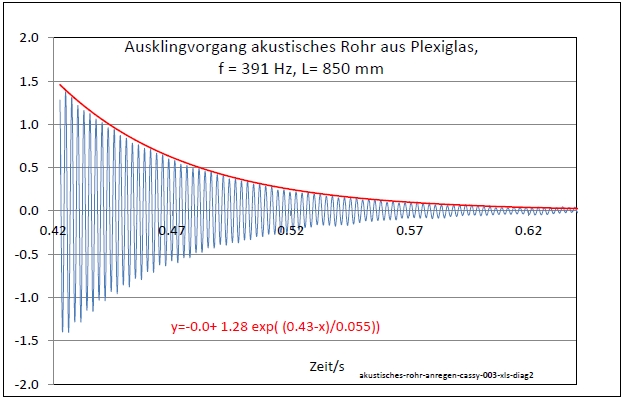 |
Abb. 00-00-40:
aus quarzrohr-angeregt.htm#kapitel-02-01-01c-6 |
0.1 Zugposaune auf das Mundstück geklatscht
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 00-01-01: Zugposaune (FB) Verfahren-2: Zur Frequenzbestimmung dient das Programm Spectrogram von R. Horne, wie hier bei der Posaune, die durch Klatschen mit der flachen Hand auf das Mundstück angeregt wurde. Die Frequenzen lassen sich mit dem Cursor auf dem Bildschirm ablesen. Der tiefste (erlaubte) Ton hat nach der Steigung der Geraden die Frequenz von 60 Hz. Profis schaffen aber auch noch einen physikalisch "verbotenen" mit etwa 32 Hz. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
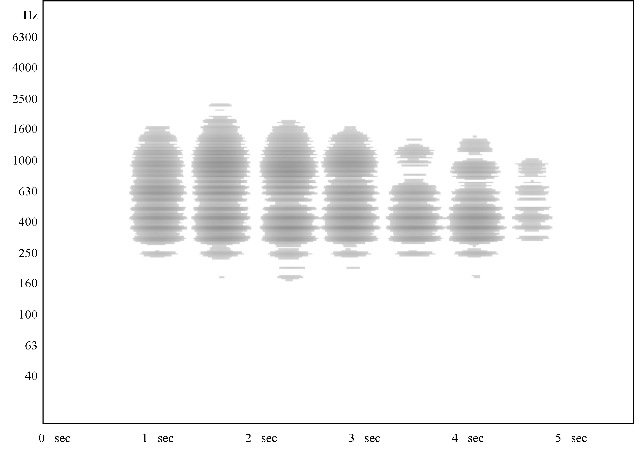
| Abb. 00-01-02: Aufnahme 20.5.2003,
mehrfach mit der Handinnenfläche auf das Mundstück geklatscht. Frequenzanalyse. Programm Spectrogram von R. Horne posaune-klatsch.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
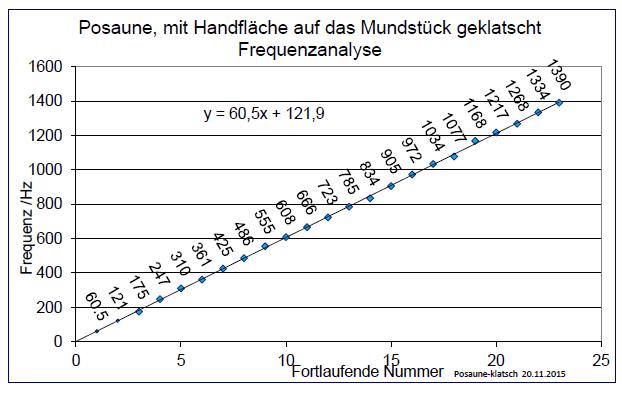
| Abb. 00-01-03: Auswertung 20.11.2015
zum vorherigen Diagramm passend wurden die Maxima auf dem Bildschirm per Hand abgelesen. posaune-klatsch.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
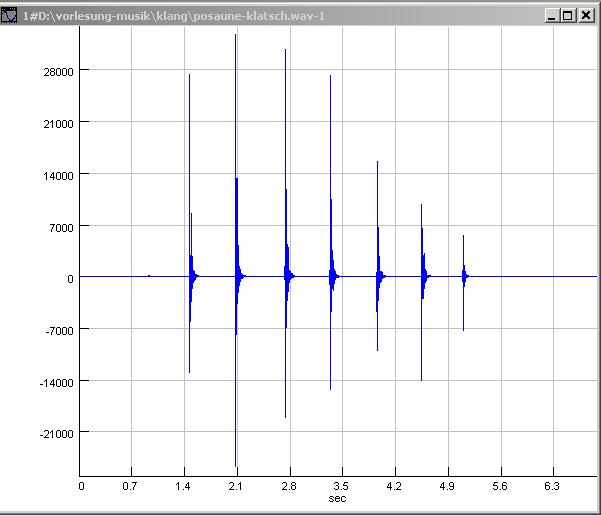
| Abb. 00-01-04: Zugposaune,
Auswertung 18.03.2020 mehrfach mit der Handinnenfläche auf das Mundstück geklatscht. Frequenzanalyse mit dem Programm SigView32 https://sigview.com/ posaune-klatsch.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
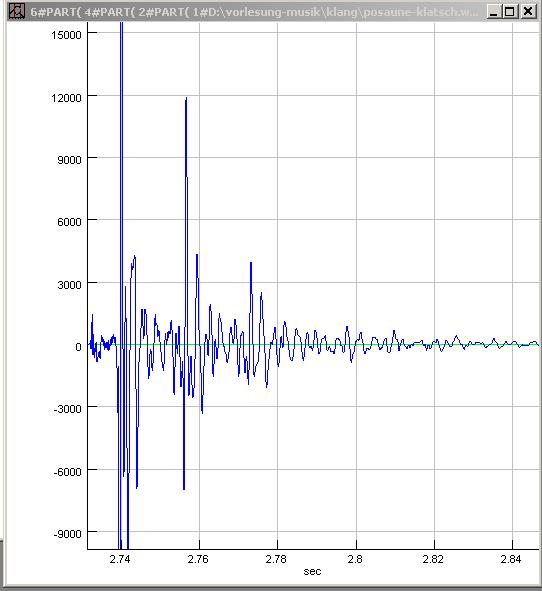
| Abb. 00-01-05: Zugposaune,
Klatsch bei 2.74 s, Analysebereich: 0,1 s posaune-klatsch.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 00-01-06: Zugposaune, Auswertung
18.03.2020 mit SigView32, Klatsch bei 2,74
s Es gibt starke und schwache Intensitäten.
blau: per Hand mit Fadenkreuz am Bildschirm abgelesen schwarz: Peak Detection automatisch durch das Programm Die Grundfrequenz (erste Harmonische) dieser Reihe bei ca. 60 Hz ist nicht ausgeprägt. posaune-klatsch.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
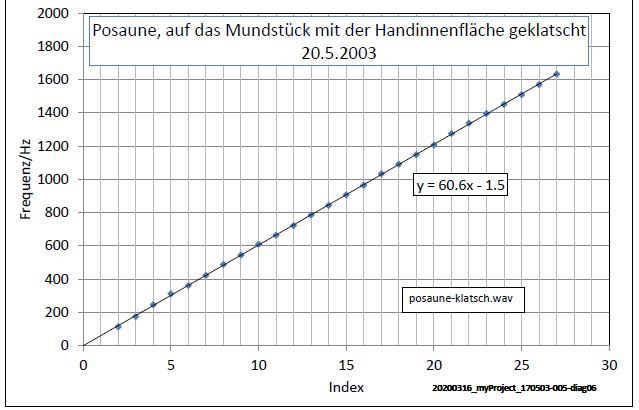
| Abb. 00-01-07: Zugposaune, Auswertung
18.03.2020, zugehöriges Diagramm (wie Abb.
01-01-03) Aus der Steigung ergibt sich ein mittlerer Frequenzabstand der Harmonischen von 60,6 Hz Nr. 1 fehlt. Bei 60 Hz ist die Intensität sehr schwach. Das Ohr ergänzt die Reihe jedoch zu einem Klangeindruck von rund 60 Hz. posaune-klatsch.wav (FB) |
0.2 Zugposaune geblasen, tiefster Ton
 |
| Abb. 00-02-01: Verfahren-1: Zugposaune, geblasen posaune-conny.wav 21.5.2003 (FB) |
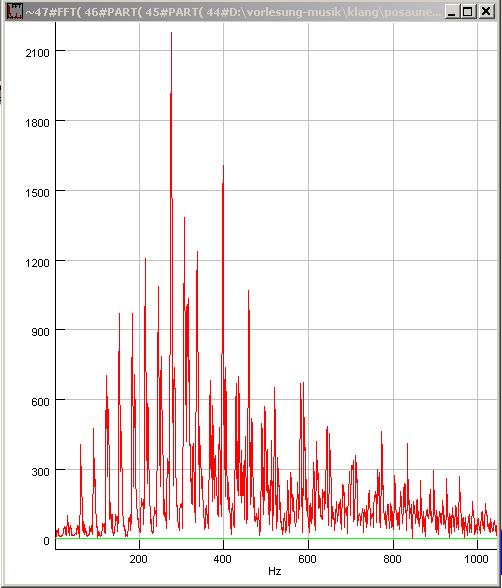 |
| Abb. 00-02-02: Zugposaune, geblasen,
Frequenzanalyse, Reihe der Harmonischen. Bei 30 Hz ist nur eine schwache Intensität zu messen (kleine Spitze links). posaune-conny.wav (FB) |
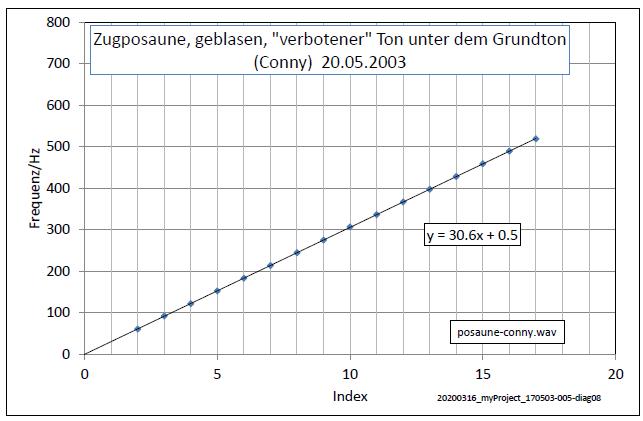 |
| Abb. 00-02-03: Reihe der Harmonischen
bei einer Zugposaune. Der tiefste Ton liegt mit einer hörbaren Frequenz von etwa 30 Hz bei der Hälfte der Grundfrequenz von rund 60 Hz. Nr. 1 fehlt. Bei 30 Hz ist nur eine sehr schwache Intensität zu messen. Das menschliche Gehirn ergänzt diese Lücke und erzeugt einen Höreindruck von 30 Hz. posaune-conny.wav (FB) |
Literatur: b-literatur.htm
 |
www.biosensor-physik.de | (c)
17.03.2020 - 03.08.2023 F.Balck |
© BioSensor-Physik 2020 · Impressum

