Beobachtungen:
Blechblasinstrument - Teil A
Materialsammlung zu
Physik und Technik
der Musikinstrumente und anderen
Schallquellen
+++++++++++++++++++++++++++
Start
A Übersicht
A0 Schall überall
A1 Ergebnisse, Tenorhorn, Frequenzen
A2 Tonhöhen und Klänge
0. Frequenzanalyse als Werkzeug
0.0 Akustische Rohre
0.0.1 Stehende Wellen auf einem Gummiseil - analog zu stehenden Wellen im Rohr
0.0.2 Schwingende Saite
0.0.3 Zahnrad
0.0.4 Akustische Rohre für Musikunterricht
0.0.5 Akustische Rohre für Physik-Anfängerpraktikum, Xylophon
0.0.6 Klarinette
0.0.6a Blockflöte
0.0.6b Querflöte
0.0.7 Stimmung, Dämpfung, Einschwingen
0.0.8 Einschwingvorgang beim Akustischen Rohr
0.1 Zugposaune auf das Mundstück geklatscht
0.2 Zugposaune geblasen, tiefster Ton
1. weitere Instrumente
1.1 Tenorhorn, Anregung mit Klatschen
1.2 Trompete mit Plastikschlauch, Anregung mit Klatschen
2. Form und Frequenzspektrum der Harmonischen
2.1 Tenorhorn geblasen
2.1a Messung vom 17.3.2020
2.1b Wiederholung am 18.03.2020
2.2 Trompete mit Plastikschlauch geblasen
2.3. Tenorhorn, Frequenzdurchlauf (Sweep)
3. Sonstige Blechblasinstrumente
4. Löcher, Klappen und Ventile
4.1 Gutes oder schlechtes Zusammenspiel von Schwingungserzeuger und Resonator
4.2 Helmholtz-Resonatoren
4.3 Frequenz und Wellenlänge bei vier Oktaven, wohltemperierte Stimmung
4.4 Verkürzung des Akustischen Resonators
4.5 Holzblasinstrumente, Aufbau, Mechanik
4.5a Blockflöte
4.5b Querflöte
4.5c Oboe
4.5d Klarinette
4.5e Saxophon
4.5f Fagott
4.6 Verlängerung des akustischen Resonators
5. Historische Meßgeräte zur Akustik
6. zwei- und dreidimesionale Klangerzeuger
6.1 Membranen
6.2 Glocken
6.3 Klangstab
++++++++++++++++++++++++++++++
A Übersicht
A0 Schall überall
 |
| Abb. A-00-01: Metallstäbe können
schwingen und dabei einen Ton erzeugen.
(Stimmgabel) (FB) |
 |
| Abb. Abb. 00-02: Eine Fahne flattert
im Wind und macht Geräusche. Auch die Wanten
(Drahtseile) erzeugen Töne, wenn der Wind stärker
weht. (FB) |
 |
| Abb. A-00-03: Rechts ist der Auslaß
von einem Ventilator. Er bläst gegen die Kante vom
gelben Klebeband, das über ein langes Kunststoffrohr
geklebt ist. Bei richtiger Luftgeschwindigkeit schwingt es und erzeugt im Rohr links einen Ton (FB) |
 |
| Abb. A-00-04: Wenn die Luftströmung
gegen die scharfe Kante bei dieser großen
Orgelpfeife trifft, dann erklingt ein Ton (FB) |
 |
| Abb. A-00-05: "Hydrodynamisches
Paradoxon": Bläst man von oben Luft in den Schlauch strömt sie zwischen den beiden Blechplattenhindurch. Die untere ist lose und hängt nur an den vier Klammern. Wenn die Strömung stark genug ist, wird die untere Platte angesaugt, bis sie gegen die obere schlägt und den Luftstrom unterbricht. Dann drückt die Luft sie herunter und es wiederholt sich der Vorgang. Dabei entsteht ein sehr lauter Ton. (FB) |
 |
| Abb. A-00-06: Ein Luftgewehr erzeugt
einen Knall (Impuls) (FB) |
 |
| Abb. A-00-07: Bringt man ihn zum
Platzen, dann hört man einen lauten Knall (FB) |
 |
| Abb. A-00-08: Wilhelm Busch |
 |
| Abb. A-00-09: Hörner / Hupen
für Fahrzeuge (FB) |
 |
Abb. A-00-10: Singvogel, Kuckuck,
Tierstimmen, menschliche Stimme,
Stimmbänder
tierstimmen.htm(FB) |
 |
| Abb. A-00-10a: Kuckuck, y-Achse: Frequenz tierstimmen.htm (FB) |
 |
| Abb. A-00-11: Umsetzung von
natürlichen Klängen und Ausgabe auf einem
Schallplattenspieler. His master's voice noch nicht ganz originalgetreu (FB) |
 |
| Abb. A-00-12: Die Rillen einer
Schallplatte zeigen die Form der Schwingungen. Zum Vergleich: in der Mitte zwei menschliche Haare (FB) |
 |
| Abb. A-00-13: Telefonhörer, Siemens
& Halske (FB) |
 |
| A-00-14: Die Membrane eines
Lautsprechers schwingt und wandelt elektrische
Signale in akustische um (FB) |
 |
| A-00-15: Piezoelektrischer
Schallgeber (Buzzer), Bariumtitanat
(BaTiO3) (FB) |
A1 Ergebnisse, Tenorhorn, Frequenzen
Seit es Computer gibt, ist eine Frequenzanalyse sehr einfach geworden.
Man nimmt einen Klang per Mikrofon auf und läßt von einem Programm herausfinden, aus welche Frequenzen er besteht.
frequenz-analyse.htm
Während bei dem Ton einer Stimmgabel nur eine einzige Frequenz auftritt, sind es bei den Musikinstrumenten meist Gruppen von Frequenzen. Die Zusammensetzung der Frequenzen, d.h. wie stark die einzelnen im Klang vorkommen (das "Kochrezept") bestimmt die Eigenschaft des Klanges.
Wenn z.B. von einer Oboe und einer Trompete der gleichen Ton zu hören ist, dann sind es unterschiedliche Mengen der "Zutaten".
Dies läßt sich gut mit synthetischen Klängen ausprobieren. Auch hier leistet der Computer gute Dienste.
frequenz-synthese.htm
Bei Blechblasinstrumenten spricht man von Naturtönen.
Dies ist eine Reihe von Frequenzen, die im Verhältnis 2, 3, 4, 5 .... usw zu einem Grundton stehen.
Es gibt also einen Grundton und dazu die Obertöne.
Im der Physik heißen die Naturtöne Harmonische, weil sie die Frequenzen eines Harmonischen Oszillators sind.
Der Grundton ist die erste Harmonische, der erste Oberton die zweite Harmonische usw.
(die Zählweise ist also um 1 verschoben).
 |
| Abb. A-01-01: Naturtöne eines
C-Instrumentes: Der Grundton ist rot markiert. Die Töne sind der Reihe nach nummeriert. Die Nummer gibt auch an, um welchen Faktor sich die Frequenz von der des Grundtones unterscheidet. Nicht alle Obertöne (Nr. 7, 9, 11, 13) klingen so "sauber", daß man sie exakt in die Notenlinien schreiben kann. (FB) |
Analysiert man nun eine der Harmonischen, dann findet man dort auch wieder eine Reihe von Obertönen.
Diese Reihe enthält nicht die Fortsetzung der Reihe über dem Grundton der Harmonischen,
sondern sie bildet wieder eine selbständige Reihe, die mit 1,2,3,4 usw. zu beschreiben ist.
Z.B. hat der erste Oberton des dritten Naturtons wieder dessen doppelte und der zweite Oberton dessen dreifache Frequenz.
Drei unterschiedliche Verfahren, die Eigenschaften des Tenorhorns zu ermitteln:
1. Blasen, Musiker erforderlich
2. Klatschen (Impuls), kann jeder
3. Anregung mit durchlaufender Frequenz (Sweep) Tondatei nötig
Alle drei liefern ähnliche Ergebnisse: die Grundfrequenz des Tenorhorns ist bei rund 60 Hz
| Verfahren-1: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. A-01-02: (Abb.
02-01-33) Verfahren-1 (geblasen): Tenorhorn, gemessene Frequenzen der ersten sechs Harmonischen (Naturtöne): Grundton und die ersten Obertöne jeweils mit ihren Reihen von Obertönen. Aus den Abständen innerhalb der Frequenzreihen ("Steigung y = ....") ergibt sich die Grundfrequenz. Auch wenn bei der untersten Kurve die erste Frequenz (Index 1) nicht vorkommt, empfindet das menschliche Ohr den Klang so, als wäre auch der entsprechende Grundton vorhanden. (Die Zeitangaben in der Legende beziehen sich auch die Position in der .WAV-Datei.)
Die Frequenzen gehorchen mathematischen Regeln. Bei Oktaven verdoppelt sich die Frequenz (B1:B2) (1:2) (B2:B3) (2:4) (F3:F4) (3:6) bei der Quinte gilt (B2:F3) (2:3) und bei der Terz (B3:D4) (4:5) 20200316_myProject_170503-005.xls |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. A-01-03: Verfahren-1:
Tenorhorn geblasen Trägt man die Steigungen der Geraden in der vorherigen Abbildung (A-01-02) gegen die Nummer des Naturtones auf, dann ergibt sich eine Gerade mit der Steigung 59,8 Hz. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Verfahren-2: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
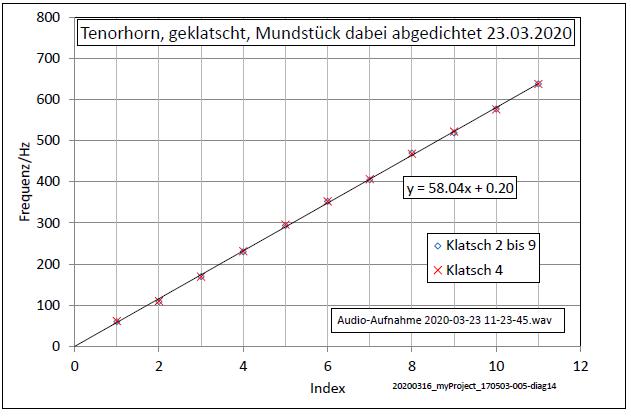
| Abb. A-01-04 (Abb.
01-01-14) Verfahren-2 (geklatscht): Tenorhorn, Frequenzen der Harmonischen,
Mittelwert der Geraden und Grundton 58,0 Hz Audio-Aufnahme 2020-03-23 11-23-45.wav (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Verfahren-3: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. A-01-05: (Abb.
02-03-11) Verfahren-3 (Sweep): Aus der Analyse entnommene Spitzenwerte. Die gefunden Werte ergeben bei ganzzahligen Indizes eine Gerade durch den Ursprung. Also müssen die stehenden Wellen symmetrisch sein, d.h. entweder an beiden Enden einen Bauch oder einen Knoten haben. Aus der Steigung der Geraden ergibt sich, daß die Obertöne einen Abstand von 60,5 Hz haben. 20200316_myProject_170503-005.xls
|
Wohltemperierte Stimmung
Das Intervall einer Oktave (Frequenz, Faktor 2) wird geometrisch in 12 gleiche Teile aufgeteilt.
Dies ergibt 12 Halbtöne mit Abstand (12. Wurzel (2)) = 1.059463 ). Das sind etwa 6 %.
Wenn man jeden Halbton in 100 Cent teilt, dann ist der Frequenzunterschied
z.B. beim Intervall A4 zu B4: Differenz von 440 Hz zu 466.2 Hz = 26,2 also 1/100 = ein Cent = 0,262 Hz
Wenn ein Stimmgerät in diesem Fall eine Abweichung von 10 Cent anzeigt, dann wären es 2,62 Hz.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
https://en.wikipedia.org/wiki/OctaveSubsubkontra-Oktave: von ‚‚‚C (8,2 Hz) bis ‚‚‚Hhttps://de.wikipedia.org/wiki/Oktave |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Unterschied von wohltemperierter und
reiner Stimmung. Für jede Harmonische wird die Frequenz ausgerechnet und diese so oft durch 2 geteilt, bis sie in dem Bereich von 440 Hz bis 879 Hz liegt. Durch Vergleich mit den Frequenzen der reinen Stimmung in dieser Oktave läßt sich ein Ton finden, der in der Nähe liegt. Die größe der Abweichung ist rechts in der Tabelle in Hz bzw. in cent angeben. Die maximale Abweichung ist beim 13. Ton mit 40 Cent, das ist nahezu ein Halbton ( 50 Cent). (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A2 Tonhöhen und Klänge
Instrumente bestehen aus zwei Bauteilen:
- Hohlraumresonator (Klangkörper)
- Schwingungserzeuger (Mundstück)
Hohlraumresonator bestimmt die Frequenzen der Schwingungen
 |
| Abb. A-02-01: Die Länge einer Pfeife
bestimmt die Tonhöhe, St. Andreas, Hildesheim Hier gibt es echte 32-Fuß-Pfeifen. (etwa 10 m lang) |
 |
| Abb. A-02-02: Die Form einer Pfeife
bestimmt den Klang. (St. Salvatoris Zellerfeld) (FB) |
 |
| Abb. A-02-03: Labialpfeifen,
unterschiedliche Formen erzeugen unterschiedliche
Klänge von oben nach unten: Prinzipal, gedackt, Spitzflöte , Rohrflöte Die Länge des Rohres bestimmt im Wesentlichen die Frequenz, wenn man von einer eindimensionalen Schwingung ausgeht, d.h. stehende Wellen bilden sich nur in Richtung der Pfeifenachse. In der Praxis ist es jedoch viel komplizierter. Auch senkrecht zum Rohr können Resonanzen auftreten. Eine lange Pfeife mit kleinem Durchmesser klingt anders als eine mit weiterem Durchmesser, obwohl sie ähnliche Grundfrequenzen haben. Mensur = Verhältnis von Weite
zur Länge
(FB) |
 |
| Abb. A-02-04: Zungenpfeifen,
Buckow-Orgel, 1862,Technikmuseum Wien (FB) |
Die Schwingungen müssen nicht nur in einer Richtung erfolgen. Sie können in einem Hohlkörper auch dreidimesional sein.
Siehe auch kapitel 6
Beispiel bei einer Hohlkugel
 |
| Abb. A-02-05: Zwei Halbkugeln aus
Aluminium (rechts) steckt man zusammen und erhält
einen geschlossenen dreidimensionalen Hohlraum
(links oben im Bild). In der einen Hälfte ist ein
Schallgeber, in der anderen ein Mikrofon
untergebracht. Beschallt man nun den Hohlraum mit
unterschiedlichen Frequenzen, dann findet man viele
Resonanzen. Durch Verdrehen der anderen Hälfte mit dem Mikrofon kann man dann herausfinden, in welchen Richtungen die zugehörigen stehenden Wellen schwingen. https://www.teachspin.com/quantum-analogs (FB) |
 |
| Abb. A-02-06: Frequenzananlyse der
Schwingungen in dem Hohlraum: Im Bereich vo 0 bis 12 kHz gibt es über 15 Resonanzen. Das grüne Objekt im oberen Fenster zeigt die Winkelverteilung der Intensität für eine vorgegebene Frequenz an. Es handelt sich um Kugelflächenfunktionen. https://de.wikipedia.org/wiki/Kugelfl%C3%A4chenfunktionen (FB) |
Schwingungserzeuger, liefert die Energie, regt die Schwingungen an.
 |
| Abb. A-02-07: Tonerzeugung bei einer
Orgelpfeife (Lippenpfeife), die Luft wird von links
kommend gegen eine Schneide geblasen. Seitenbleche
und Einkerbungen bestimmen Klang und
Ansprechverhalten. orgelpfeife.htm (FB) |
 |
| Abb. A-02-08: Familie von
Blockflöten, Sopran, Alt und Tenorflöte (FB) |
 |
| Abb. A-02-09: Die Luft kommt von
links aus dem Windkanal heraus und trifft auf die
Schneide. (FB) |
 |
| Abb. A-02-10: Querflöte: Die Öffnung
hat am oberen Rand eine scharfe Kante (Schneide) Der Flötenspieler bläst die Luft gegen die Kante (FB) |
 |
| Abb. A-02-11: Zungen in einer
Mundharmonika. Beim Blasen schwingen sie und
öffnen/schließen dabei periodisch den Weg für die
Atemluft des Spielers. (FB) |
 |
| Abb. A-02-12: verschiedene Zungen von
Ziehharmonikas, Harmonium . . . die oberen sind mit Zusatzmassen versehen, damit sie mit niedrigen Frequenzen schwingen. (FB) |
 |
| Abb. A-02-13: Zungenpfeife einer Orgel, rechts die Zunge, die die Frequenz vorgibt und links der Schallbecher, der den Klang bestimmt. Rechts fehlt der "Stiefel", der die Luft zuführt. (FB) |
 |
| Abb. A-02-14: Zungenpfeife
einer Orgel, Eine dünne Blechzunge aus Bronze ist links eingespannt und deckt die Öffnung in dem Messingkörper nahezu ab. Der Messingkörper ist hohl. Von rechts einströmende Luft kann nach links durch den Pfeifenkörper bis zum Trichter der Pfeife gelangen. Dort wird der Schall abgestrahlt. Mit dem Messingdraht läßt sich die Länge der Blechzunge verändern (stimmen) (FB) |
 |
| Abb. A-02-15: Mundstück und Rohrblatt
bei einer Klarinette. Das Blatt wird über die
Öffnung gebunden und steht ein wenig ab, so daß Luft
hineinströmen kann. Bei passendem Andruck und
Blasstärke schließt und öffnet sich der Spalt
zwischen Blatt und Mündstück periodisch. Dabei
entsteht ein Ton. Abb. 15-17 in frequenz-analyse.htm (FB) |
 |
| Abb. A-02-16: Klarinettenmundstück,
das Rohrblatt ist aufgebunden und steht an der
Spitze etwa einen halbem Millimeter ab. (FB) |
 |
| Abb. A-02-17: Zwei Doppelrohrblätter
für eine Oboe (ähnlich beim Fagott). Beim
Spielen werden die beiden Rohre leicht mit den
Lippen zusammengedrück. Durch die hindurch gepreßte
Luft verschließt sich der Spalt zwischen ihnen
periodisch und es entsteht ein Ton. (FB) |
 |
| Abb. A-02-18: Mundstücke von
Blechblasinstrumenten. Unterschiedliche Größe der
Kessel und der nahezu konischen Bohrung. Die Lippen des Spielers bilden beim Blasen das schwingende Element, das den Luftstrom periodisch unterbricht. (FB) |
 |
| Abb. A-02-19: Mundstücke Trompete, Tenorhorn 15 T-S, 12 T-S und 6 1/2 T-S (unterschiedliche Weite des Kessels) (FB) |
 |
| Abb. A-02-20: Mundstücke Trompete, Tenorhorn 15 T-S, 12 T-S und 6 1/2 T-S (FB) |
Literatur: b-literatur.htm
 |
www.biosensor-physik.de | (c)
17.03.2020 - 26.10.2023 F.Balck |
© BioSensor-Physik 2026 · Impressum
