Beobachtungen:
Beschleunigte und abgebremste Ladungen
Ändert ein Teilchen mit Ladung seinen Bewegungszustand, d.h. Veränderung von Geschwindigkeit oder Richtung der Bewegung, so tritt eine elektromagnetische Strahlung auf.
1. Übersicht
1.1
1.2 träge und schwere Massen
2. Dipol
3. Ablenkung ohne elektrisches Feld, Aufspaltung durch Erdmagnetfeld?
4. Einfluß der Erdachse auf andere Objekte
4.1 Dipol
4.2 Helmholtz-Spule
4.3 Spule mit Lichtleiter
5.
Beugung
5.1 Beugung am Drahtgitter
5.2
Beugung an Loch und Scheibe
5.3
Beugung an Stäben
5.4
Beugung beim Doppelspalt
5.5
Beugung an zwei Stäben
5.6 Rotation um
lotrechte Achse
5.6.1
Rotation
um lotrechte Achse, Beugung
an einem Aluminium-Stab
5.6.2
Rotation um lotrechte Achse,
Beugung an einem Drahtgitter
5.7
Beugung an einem Stab,
unterschiedliche
Materialien
5.7.1
Ablesung direkt während
der Beobachtung
5.7.2
Markierung der
Positionen auf
Holzbrett
5.8
Linsen
7. Resonanzrohr
7.1 Resonanzrohr im Einsatz
Einfluß der Frequenz
7.2 Unterschiedliche Materialien am Eingang des Rohres
8. Ringe und Spulen
9. Effekte durch natürliche Anregung
9.1 Durchstrahlung
9.2 SEUMS direkter Link zur Zusammenfassung seums.htm
9.3 Anregung mit Objekten
9.4 Anregung mit elektrischen Feldern
10. Sonstige aktive Körper
1. Übersicht
Änderung der Geschwindigkeit:
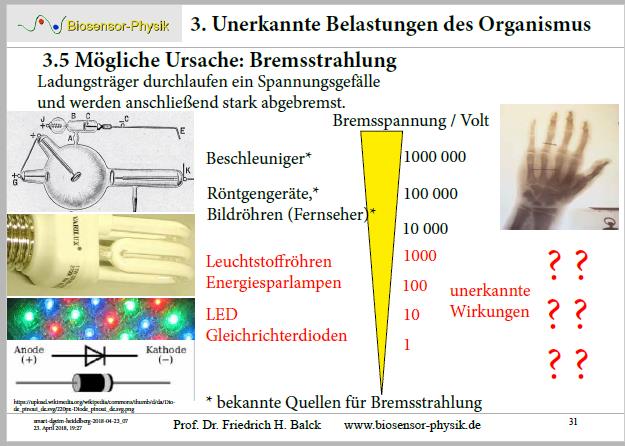
Bei vielen technischen Anwendungen (Beleuchtungskörpern, Halbleiterelektronik) kommt es zur Beschleunigung oder Abbremsung von Elektronen oder ionisierten Gasen mit vergleichsweise geringen Energiedifferenzen. Die Spannungsdifferenz beträgt einige Volt bis einige Hundert Volt.
Bei Röhrenfernsehern oder Röntgenanlagen im medizinischen Bereich sind die Beschleunigungsspannungen etwa 20 kVolt.
In großtechnischen Forschungseinrichtungen arbeitet man mit 1 MVolt und höher.
Bei der Kernspaltung treten sehr viel größere Energien auf, die auch zu starken Beschleunigungen von geladenen Elemetarteilchen führen.
Änderung der Richtung:
Energiesparlampen mit gewendeltem Entladungsrohr,
Forschungsgeräte: Fadenstrahlrohr, Cyclotronbeschleuniger, Synchrotronbeschleuniger, Undulator
Kernspaltung, Teilchen: alpha-, beta-, gamma-Strahlung
Bei Spannungen unterhalb von 1000 Volt sind bisher keine Beschleunigungs- oder Bremsstrahlungen mit Meßgeräten nachgewiesen worden.
Es wäre aber denkbar, daß auch die bei einigen Volt abgebremste Ladungsträger in einer Halbleiterdiode oder LED eine Art Strahlung aussenden.
Das wären dann "die kleinen Brüder der Röntgenstrahlung".
s.a. /Gebbensleben 2010/ /Kernbach (1) 2013/
Bedingt durch die Miniaturisierung bei Festkörper-Halbleitern und deren perfektem kristallinen Aufbau entsteht eine nahezu punktförmige Quelle für die Strahlung. Dies kann zu höheren Strahlungsdichten und möglicherweise auch zu Kohärenzen führen.
Bei organischen Materialien für LEDs (OLED) könnte die "Bremsstrahlung" eine andere Qualität haben.
OLED-Fernseher gibt es schon auf dem Markt. Sie erzeugen sehr viel weniger spürbare Belastung als Halbleiter-LED-Bildschirme.
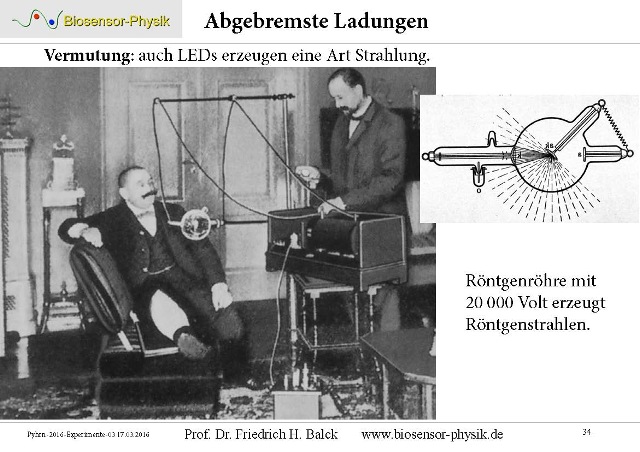 |
| Abb. 01-01: Abgebremste
Ladungen mit hoher Energie (20 000 eV) erzeugen
Strahlung. Eine nicht abgeschirmte Röntgenröhre hängt an einem Gestell und belichtet den Film, der unter dem Oberschenkel der Person liegt. Auch der Arzt setzt sich ungeschützt der Röntgenstrahlung aus. |
 |
| Abb. 01-02: Auch bei niedrigen Spannungen (500 V, 3 V oder 1 V) kommt eine unsichtbare "Strahlung" heraus. Bei der Gasentladungsröhre (r.o.) zeigen die beiden gelben Linien die Begrenzung dieser "Strahlung". (FB) |
"Bremsstrahlung ist die elektromagnetische Strahlung, die entsteht, wenn ein geladenes Teilchen, zum Beispiel ein Elektron, beschleunigt wird. Jede Geschwindigkeitsänderung eines geladenen Teilchens erzeugt Strahlung. Von Bremsstrahlung im engeren Sinne spricht man, wenn Teilchen in Materie gebremst werden."
https://de.wikipedia.org/wiki/Bremsstrahlung
"Bremsstrahlung (German pronunciation: [ˈbʁɛmsˌʃtʁaːlʊŋ] ( listen), from bremsen "to brake" and Strahlung "radiation", i.e. "braking radiation" or "deceleration radiation") is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the accelerated particles increases.
Strictly speaking, braking radiation is any radiation due to the acceleration of a charged particle, which includes synchrotron radiation, cyclotron radiation, and the emission of electrons and positrons during beta decay. However, the term is frequently used in the more narrow sense of radiation from electrons (from whatever source) slowing in matter.
Bremsstrahlung emitted from plasma is sometimes referred to as free/free radiation. This refers to the fact that the radiation in this case is created by charged particles that are free, i.e. not part of an ion, atom or molecule, both before and after the deflection (acceleration) that caused the emission." https://en.wikipedia.org/wiki/Bremsstrahlung
Röntgenstrahlung
X-radiation (composed of X-rays) is a form of electromagnetic radiation. Most X-rays have a wavelength ranging from 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz (3×1016 Hz to 3×1019 Hz) and energies in the range 100 eV to 100 keV. X-ray wavelengths are shorter than those of UV rays and typically longer than those of gamma rays. In many languages, X-radiation is referred to with terms meaning Röntgen radiation, after Wilhelm Röntgen,[1] who is usually credited as its discoverer, and who had named it X-radiation to signify an unknown type of radiation.[2] https://en.wikipedia.org/wiki/X-ray
Cyclotronstrahlung
Cyclotron radiation is electromagnetic radiation emitted by moving charged particles deflected by a magnetic field. The Lorentz force on the particles acts perpendicular to both the magnetic field lines and the particles' motion through them, creating an acceleration of charged particles that causes them to emit radiation as a result of the acceleration they undergo as they spiral around the lines of the magnetic field. https://en.wikipedia.org/wiki/Cyclotron_radiation
Synchrotronstrahlung
"The electromagnetic radiation emitted when charged particles are accelerated radially () is called synchrotron radiation. It is produced, for example, in synchrotrons using bending magnets, undulators and/or wigglers. It is similar to cyclotron radiation except that synchrotron radiation is generated by the acceleration of ultrarelativistic charged particles through magnetic fields. Synchrotron radiation may be achieved artificially in synchrotrons or storage rings, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over the entire electromagnetic spectrum." https://en.wikipedia.org/wiki/Synchrotron_radiation
Anwendungen bei unterschiedlicher Bremsspannung.
Halbleiterdioden
Gasentladungen
gebogener Elektronenstrahl
Röntgenröhren
Beschleuniger
 |
| Abb. 01-03: Gleichrichterdiode.
Spannungsabfall am pn-Übergang im Betrieb ca. 1 Volt s.a. /Gebbensleben 2010/ hyperschall.htm (FB) |
 |
| Abb. 01-04: Verschiedene LEDs. Im
Betrieb gibt es einen Spannungsabfall von rund 3
Volt. (FB) |
 |
| Abb. 01-05: blaue Leds,
Spannungsabfall im Betrieb ca. 3 Volt. (FB) |
 |
| Abb. 01-06: Gasentladungsrohr,
schwach evakuiert. Zwischen den beiden
Ringelektroden liegt eine Spannung von rund 600 V.
Es gibt eine Entladung mit scheibenförmig
erleuchteten Bereichen. gasentladung.htm (FB) |
 |
| Abb. 01-07: Gasentladungsrohr. An
beiden Enden des Rohres gibt es einen kegelförmigen
Bereich, in dem spürbar etwas herauskommt. (FB) |
 |
| Abb. 01-08: Spektrallampe, mit Neon
gefüllt. Spannungsabfall ca. 400 Volt (FB) |
 |
| Abb. 01-09: Leuchtstofflampe, nur im
rechten Teil ist der Leuchtstoff auf das Glas
aufgebracht. Es brennt eine Entladung (Plasma) mit
UV-Lichtanteil. (FB) |
 |
| Abb. 01-10: Leuchtstäbe,
Kaltkathodenlampen, Hintergrundbeleuchtung für
LCD-Bildschirme, Brennspannung ca. 500 Volt (FB) |
 |
| Abb. 01-11: Energiesparlampen
unterschiedlicher Bauart. Die Röhren sind teilweise
gebogen. Die Ladungen werden bei den Bögen
beschleunigt, weil sie dort ihre Richtung ändern
müssen. (FB) |
 |
| Abb. 01-12: Energiesparlampe mit
gewendelter Röhre. Die Ladungen bewegen sich auf
kreisförmigen Bahnen (Kreisförmige Beschleunigung)
und erfahren bei den beiden Richtungswechseln im
vorderen Bereich eine erhöhte Beschleunigung. (FB) |
 |
| Abb. 01-13: Fadenstrahlrohr: Ein
Elektronenstrahl kommt aus einer Glühkathode, wird
mit etwa 250 V beschleunigt und verläßt den Aufbau
durch eine kleine Öffnung. Die spezielle Gasfüllung
in dem Glaskolben macht den Strahl sichtbar (FB) |
 |
| Abb. 01-14: Fadenstrahlrohr: Legt man
ein statisches Magnetfeld an, so laufen die
Elektronen auf Kreisbahnen, wenn Strahlachse und
Achse des Feldes exakt senkrecht zueinander stehen.
Sind sie etwas verkippt zueinander, gibt es eine
Spiralbahn. (FB) |
 |
| Abb. 01-15:
Oszillograph. Ein Elektronenstrahl wird
beschleunigt, trifft auf einen Leuchtschirm auf und
wird dabei abgebremst. Bei feststehendem Strahl ist
in Strahlachse noch in vielen Metern Entfernung vor
und hinter dem Gerät etwas zu spüren. Auch bei älteren schwarz-weiß Fersehern, die noch keine Lochmaske aus Metall vor dem Leuchtschirm haben, dürften die gleichen Effekte auftreten. (FB) |
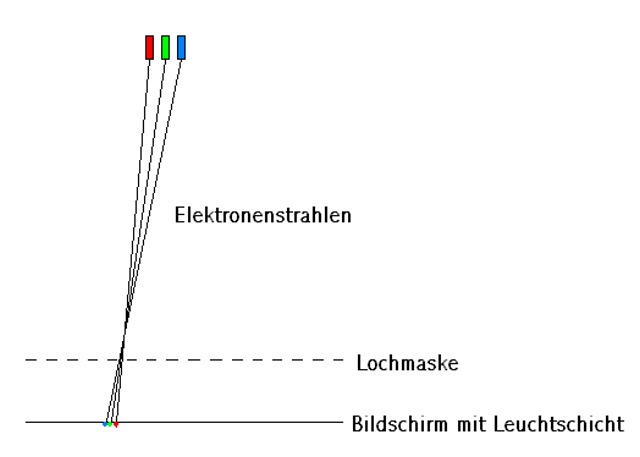 |
| Abb. 01-16: Farbfernseher. Die
Elektronenstrahlen von drei Röhren treffen auf eine
Lochmaske aus Metall. Dabei entstehen
Röntgenstrahlen, die von der speziell konstruierte
Frontscheibe zurückgehalten werden.
https://upload.wikimedia.org/wikipedia/de/1/1c/Farbbildschirm.PNG |
 |
| Abb. 01-17: Geißler-Röhren, Glasrohr
mit verdünnten Gasen und Hochspannung https://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Geissler_tubes.jpg/1200px-Geissler_tubes.jpg |
|
|
| Abb. 01-18: Crookes Röhre https://en.wikipedia.org/wiki/Crookes_tube |
 |
| Abb. 01-19: Experiment zum Studium
der ionisierenden Wirkung der Röntgenstrahlen, von links: Funkeninduktor, Crookes- Entladungsrohr, Elektrometer, Amperemeter, Fernrohr zur Beobachtung des Elektrometers, (Brachner S. 85) |
 |
| Abb. 01-20: Röntgens
Versuchsanordnung zur Prüfung der Durchlässigkeit
verschiedener Stoffe links: Elektrometer, mitte: Röntgenröhre, rechts: Funkeninduktor (/Brachner 1995/, S. 39) |
 |
| Abb. 01-21: Röntgenröhre. Von rechts
kommen die Elektronen, werden nach links
beschleunigt und treffen auf die schräggestellte
Anode auf. Dabei entsteht Röntgenstrahlung. Weitere Informationen zu den Anschlüssen, Regenerierung, harte, weiche Röhren .... roentgen.htm (FB) |
 |
| Abb. 01-22: Röntgenröhre. Von rechts
(k) kommen die Elektronen, werden nach links
beschleunigt und treffen auf die schräggestellte
Anode (ak) auf. Dabei entsteht Röntgenstrahlung.
(Meyers Lexikon 1929) |
 |
| Abb. 01-23: Aufnahme des
Unterschenkels (1905) mit einer transportablen
Röntgeneinrichtung. Strahlenschutz gibt es nicht. (/Brachner 1995/, S. 70) |
 |
| Abb. 01-24: Ausbildung von
Röntgenassistenten im Röntgenlabor des
Lette-Vereins. Die linke Person steht mit ihrem Rücken vor einer Röntgenröhre. Die anderen Personen betrachten das Bild des Brustkorbs auf einem Leuchtschirm. Strahlenschutz gibt es nicht. (/Brachner 1995/, S. 84) |
 |
| Abb. 01-25: Festkörperphysik mit
Röntgenstrahlung, links die Röntgenröhre, rechts ein
Goniometer (Probenhalter mit Winkelverstellung in
mehreren Achsen) mit der zu untersuchenden Probe. Versuchsanordnung zur Röntgenbeugung von W.Friedrich, P.Knipping und Max von Laue, 1912, Deutsches Museum (FB) |
 |
| Abb. 01-26: Röntgenversuche mit einer
Crookes Röhre. rechts oben: Betrachtung der Hand mit einem Leuchtschirm unten: Belichtung eines Films mit dem Bild der Hand "Taking an X-ray image with early Crookes tube apparatus, late 1800s. The Crookes tube is visible in center. The standing man is viewing his hand with a fluoroscope screen. No precautions against radiation exposure are taken; its hazards were not known at the time." https://en.wikipedia.org/wiki/X-ray https://en.wikipedia.org/wiki/X-ray#/media/File:Crookes_tube_xray_experiment.jpg |
 |
| Abb. 01-27: Ein
Elektronenstrahl verläuft in einem homogenen Feld.
Feld und Strahlachse stehen senkrecht aufeinander.
Die Ladungen behalten ihre Geschwindigkeit bei, aber
die Bewegungsrichtung ändert sich. https://upload.wikimedia.org/wikipedia/commons/5/58/Syncrotron.png |
 |
| Abb. 01-28:
Undulator: Ein Elektronenstrahl geht durch eine
Barriere mit wechselnden Magnetfeldern. Dabei
entstehen Bahnen mit kreisförmigen Abschnitten. Dort
ändert sich die Bewegungsrichtung mehrmals
(Beschleunigung). Dabei bildet sich eine
Strahlung.
https://upload.wikimedia.org/wikipedia/commons/9/9f/Undulator.png |
 |
| Abb. 01-29: Linearbeschleuniger. Ein
elektrisches Wechselfeld und Beschleunigungsstrecken
mit zunehmender Länge sorgen dafür, daß die
geladenen Teilchen auf ihrem Weg eine größere
Geschwindigkeit bekommen. Die beiden Zustände (obere und untere Bildhälfte) wechseln sich zeitlich nacheinander ab. https://upload.wikimedia.org/wikipedia/commons/2/25/Lineaer_accelerator_en.svg |
Funkantennen, Dipol
 |
| Abb. 01-30: Kleiner Dipol aus zwei
Messingdrähten, der zugehörige Sender liefert
Frequenzen im Kilohertz-Bereich. Während die
Magnetfelder der beiden Zuleitungen entgegengesetzt
sind und sich "auslöschen", strahlen jeder der
beiden Drähte abwechselnd ein elektrisches und ein
magnetisches Feld ab. Die Ladungen werden im Draht
periodisch beschleunigt und abgebremst. (FB) |
 |
Abb. 01-31: Große Dipolantennen im
Megahertz-Bereich (FB)aus |
Beschleunigte Ladungen bei Windkraftanlagen
Die Rotorblätter sind überwiegend aus nichtleitendem Kunststoff. Für den Blitzschutz sind Metallbänder oder Metallstreifen eingearbeitet. Durch die Reibung mit der Luft kann es Reibungselektrizität geben, die zu unterschiedlicher Ladungsverteilung auf den Flügeln kommt. Wegen der Kreisbewegung gibt es eine ständige Radialbeschleunigung.
 |
| Abb. 01-32: Der Rotor dieser
Windkraftanlage hat einen Durchmesser von 112 Metern
- eine der ersten Anlagen dieses Typs (FB) |
 |
| Abb. 01-33: Nach Absturz eines
Rotorblattes kann man einige Details der
Konstruktion erkennen: Glasfaserverstärkter Kunststoff, Holz und in zwei Streifen verlegte Blitzableiter. (FB) |
 |
| Abb. 01-34: Aluminiumstreifen als
Blitzschutz (FB) |
Beschleunigte Ladungen bei Kernreaktionen
Das Kerkraftwerk Krümmel an der Elbe wird zurückgebaut. Radioaktive Strahlung sollte es nicht geben, dennoch findet man spürbare Strukturen, die sowohl vom Reaktorblock als auch vom Zwischenlager ausgehen.
Da bei der Kernspaltung auch große Kräfte entstehen, dürften die Ladungen in den Atomen Beschleunigungen ausgesetzt sein.
Sind die bei der Spaltung entstehenden Antineutrinos als Folgeprodukte von Beschleunigungen anzusehen?
Antineutrinos sind nur sehr schwer nachzuweisen.
kruemmel.htm
 |
| Abb. 01-35: Das Zwischenlager östlich vom Reaktorblock (FB) |
 |
| Abb. 01-36: Das große Foto gibt einen Eindruck vom Innenleben des Reaktorgebäudes. (FB) |
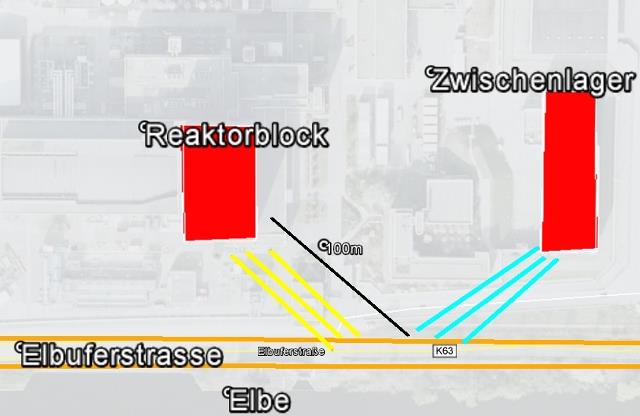 |
| Abb. 01-37: schematisch: Beim Gehen entlang der Elbuferstrasse gibt es mehrere Gruppen von spürbaren Streifen, die aus zwei unterschiedlichen Richtungen kommen, aus dem Reaktorblock (gelb) und aus dem Zwischenlager (türkis). Die Entfernung bis zur Straße (schwarze Linie) beträgt etwa 100 Meter (FB) |
Beobachtungen Mai 2012
Das Kraftwerk ist dauerhaft vom Netz, es wird zurückgebaut.
Obwohl der Reaktor nicht mehr im Betrieb ist, waren beim Gehen entlang der Elbuferstraße einige mehrere Meter breite spürbare Streifen wahrzunehmen, die in mehreren Gruppen auftraten. (Abb. 19)
Ein Teil der Streifen war so ausgerichtet, daß er zum Reaktorblock und der andere Teil in Richtung auf das Zwischenlager zeigte.
Offensichtlich kommen von den Zerfallsreaktionen in den nicht mehr aktiven, abklingenden Brennelementen weiterhin Teilchen heraus, deren Wirkung man noch in hundert Meter Entfernung spüren kann.
Ist das die Strahlung, die noch bis zum anderen Elbufer reicht und dort die Ursache für die erhöhte Erkrankungsrate von Leukämie bei Kindern darstellt?
Erhöhte Radioaktivität in 300 Metern Entfernung hat man nicht gemessen.
Es gibt aber noch andere Zerfallsprodukte, z.B. die Antineutrinos beim beta(-) Zerfall. http://de.wikipedia.org/wiki/Neutrino
Möglicherweise sind die Antineutrinos spürbar.
Antineutrinos
Demtröder Band IV Seite 48 /Demtröder 2005/
Als dann das Neutron 1932 von Chadwick als Baustein der Atomkerne mit einer Masse mn ≈ mp entdeckt wurde, war schnell klar, dass es sich beim β-Zerfall um ein anderes neutrales Teilchen handeln musste, dessen Masse wesentlich kleiner, sogar kleiner als die des Elektrons ist, weil sonst nicht die maximale Energie E(β) ≈ Emax im β-Energiespektrum auftreten kann.Demtröder Band IV Seite 163
Deshalb wurde das hypothetische Teilchen Neutrino ν (kleines Neutron) genannt. Aus Symmetriegründen muss es dann, wie bei allen Elementarteilchen auch ein entsprechendes Antiteilchen, das Antineutrino ¯ν geben
Insgesamt werden daher 201MeV Energie frei, von denen die unbeobachtbare Antineutrinoenergie entweicht.Demtröder Band IV Seite 174
Ursprünglich nahm man an, dass es nur eine einzige Sorte von Neutrinos ν mit ihren Antiteilchen ¯νgibt. Es stellteDemtröder Band IV Seite 199
sich dann aber heraus, dass es drei verschiedene Neutrinoarten mit jeweils einem Antineutrino gibt:
Das Elektron-Neutrino νe,¯ν e, das Myon-Neutrino νμ, ¯νμ und das τ-Neutrino ντ ,¯ντ
Solche Teilchen werden linkshändig genannt. Alle Antineutrinos haben dagegen positive Helizität, sie sind rechtshändig.
 |
| Abb. 01-38: smart-dgeim-heidelberg-2018-04-23_07.pdf |
 |
| Abb. 01-39: smart-dgeim-heidelberg-2018-04-23_07.pdf |
 |
| Abb. 01-40: smart-dgeim-heidelberg-2018-04-23_07.pdf |
 |
| Abb. 01-41: smart-dgeim-heidelberg-2018-04-23_07.pdf |
 |
Abb. 01-42:aus felder.htm#kapitel-04-07-01c |
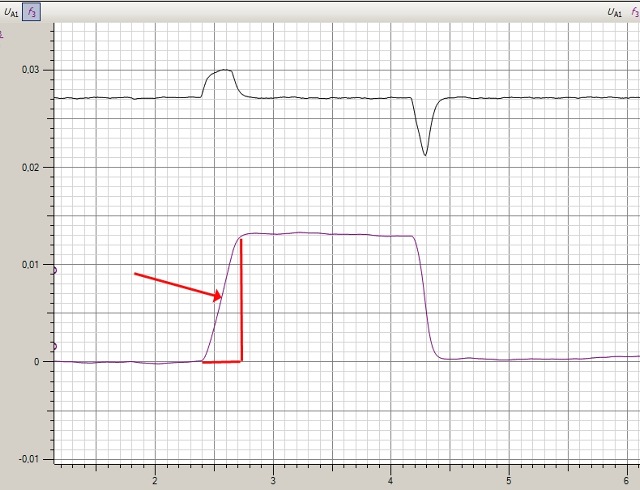 |
Abb. 01-43:aus felder.htm#kapitel-04-07-01c |
1.2 Träge und schwere Massen
Bei massebehafteten Teilchen sind acht verschiedene Kombinationen möglich
ohne / positive / negative schwere Masse
ohne / positive / negative träge Masse
| nicht schwer |
positiv schwer |
negativ schwer |
|
| nicht träge |
|
x |
x |
| positiv träge |
x |
x |
x |
| negativ träge |
x |
x |
x |
Am Beispiel eines Kettenkarussels lassen sich die Unterschiede verdeutlichen.
 |
| Abb. 01-44: +
schwer
+schwer +
träge
+träge
(FB) |
 |
| Abb. 01-45: -schwer
-schwer +träge
+schwer -träge -schwer
-träge -träge (FB) |
2. Dipol, Ablenkung der "Strahlung" mit elektrischem Feld
Ergebnis:
An der Spitze des Dipols kommen geladene Teilchen heraus, die sich im elektrischen Feld ablenken lassen.
Sie verhalten sich änlich wie die beim Experiment mit der Gleichrichterdiode.
Aufbau der Ablenkeinrichtung wie bei der Gleichrichterdiode in konische-koerper.htm#kapitel-04-01a
Es gelten ähnliche Regeln wie bei einer horizontal gewordenen Masse, die dem Einfluß der Erdbeschleunigung unterliegt. Sie fliegt auf einer Parabel fliegt.
- Je höher die Anfangsgeschwindigkeit, um so geringer die Ablenkung.
- je stärker die zur Bewegung senkrechten Beschleunigung, um so stärker die Ablenkung.
- Das Vorzeichen der Beschleunigung bestimmt die Richtung der Ablenkung.
Für das Experiment: Die Ziehrichtung des Drahtes sollte bei beiden Dipolhälften gleich sein.
(d.h. aus einem langen Draht zwei Teile machen und die Orientierung beibehalten.)
 |
Abb. 02-01: Ablenkeinrichtung durch
elektrische Felder bei einem Oszillograph. aus kuehlwasser-achtzehn-06.htm#kapitel-06 |
 |
Abb. 02-01a: Ablenkung des
Strahls von einer Gleichrichterdiodeaus konische-koerper.htm#kapitel-04-01 |
 |
| Abb. 02-02: Ein Dipol aus Messing.
Von den Spitzen geht etwas aus, das sich mit einem
elektrischen Feld ablenken läßt. Der rechte Stab ist am Signalausgang, der linke am Massepol des Generators angeschlossen. (FB) |
 |
| Abb. 02-03: Maßstab zum Vergleich Länge des Dipols: 16 cm, Abstand der Platten: 5 cm (FB) |
 |
| Abb. 02-04: linkes Instrument:
Ablenkspannung 1.6798 V, rechtes Instrument: Signalamplitude 0.1922 V RMS darunter: Gleichstromquelle, Frequenzgenerator Dreieck, 4,88 Hz (FB) |
 |
| Abb. 02-05: Ausgangsspannung vom
Generator: Dreieck z.B. mit 5 Hz und 2
Hz Bei der roten Kurve steigt die Spannung langsamer an. (FB) |
Vereinfachung: der Dipol soll durch einen Plattenkondensator angenähert werden. Wenn die Spannung beim Dipol mit der Zeit dreieckförmig ansteigt und abfällt, dann verhält sich auch die Beschleunigung entsprechend.Beschleunigung eines geladenen Teilchens im elektrischen Feld eines Plattenkondensators. D.h. die Beschleunigung steigt und fällt zeitlich linear zwischen einem positiven und einem negativen Grenzwert periodisch hin und her. |
 |
| Abb. 02-06: Der "Strahl" wird in 1.15
m Entfernung vor dem Maßstab verfolgt und jeweils
dessen linke und rechte Position notiert. Er hat
etwa in dem Abstand eine Breite von 10 cm. Im
Nahbereich gelten für die Breite etwa die kleinen
Holzstäbe. (FB) |
 |
| Abb. 02-07: Ablenkwinkel als
Funktion der Frequenz für positive und negative
Polung der Platten. Die kurzen Striche geben die gemessenen Randpositionen wieder, die Raute ist deren Mittelwert. Die schwächeren Markierungen bei 15 Hz gehören zu beiden nachfolgenden Abbildungen bei unterschiedlichen Signalamplituden und Ablenkspannungen. Ergebnis:
Bei dem Dreieckssignal ist die Beschleunigung für eine halbe Periode jeweils konstant sowohl beim Anstieg als auch beim Abfall. Verwendet man statt des Dreiecks ein Sinussignal, dann ist die Struktur sehr aufgeweicht. (FB) |
 |
| Abb. 02-08: Ablenkwinkel als Funktion
der Signalspannung. Ergebnis: Die Wirkung der Ablenkung wird mit zunehmender Spannung kleiner. Je größer die Signalspannung umso stärker ist die Beschleunigung und damit sinkt der Einfluß der Ablenkung. (FB) |
 |
| Abb. 02-09: Ablenkwinkel als Funktion
der Ablenkspannung. Ergebnis: Mit zunehmendem Betrag der Spannung wird die Ablenkung größer. (FB) |
 |
| Abb. 02-10: Die Enden sind flach
gefeilt. 06.04.2020 (FB) |
 |
| Abb. 02-11: Dipol 32 cm Länge, reicht
bis zum Strich, 4 cm vor den Aluplatten (FB) |
 |
| Abb. 02-12: alle Dipole 11 cm, 16 cm
und 32 cm Länge, der kurze reicht bis zum Strich vor
den Aluplatten. (FB) |
 |
| Abb. 02-13: Die Länge des Dipols
hat einen Einfluß. Bei kurzen Dipolen scheint die Beschleunigung höher als bei langen zu sein - bei sonst gleichen Eigenschaften. Beobachtung:
Begründung Wenn in dem Messingdraht Ladungsträger durch Anlegen einer Spannung U beschleunigt werden, dann steckt die elektrische Feldstärke E dahinter. Beide Größen sind über eine Länge L miteinander verknüpft. E = U / L Bei einem langen Draht ist die Feldstärke kleiner als bei einem kurzen. Also ist die Beschleunigung bei langen Drähten kleiner. Bei höherer Frequenz ist erfolgt der Anstieg der Dreiecksflanken schneller. D.h. dann ist die Beschleunigung ebenfalls größer. 06.04.2020 (FB) |
Wie hängt die Länge der Beschleunigungsstrecke damit zusammen? |
 |
| Abb. 02-14: Unter dem Einfluß der
Schwerkraft ist die Bahn dieser Wasserstrhlen
parabelförmig. Je größer der Druck ist, um so weniger gekrümmt ist die Bahn des Wassers. (FB) aus bbewegte-materie.htm#kapitel-03-03 |
3. ?????ß Einfluß der Erdachse
Der "Forschungsgarten" hat eine geografische Breite von 49.63°
Es wirkten folgende Kräfte:
1. Schwerkraft
2. Zentrifugalkraft durch die Erdrotation
3. Erdmagnetfeld
Die Schwerkraft ist um den Faktor 300 größer als die Zentrifugalkraft.
Die Richtung der Schwerkraft ist senkrecht zur Erdoberfläche. Sie wirkt auf schwere Massen.
Die Richtung der Zentrifugalkraft zeigt am Äquator senkrecht nach oben, also senkrecht zur Erdoberfläche
und z.B. bei der geografischen Breite 50° vom Lot aus gesehen 50° in Richtung Süden.
Sie wirkt auf träge Massen.
Das Erdmagnetfeld wirkt auf magnetische Dipole (Kompaßnadel). Es hat hier in Deutschland bei 50° geografischer Breite etwa die Richtung 60° (Inklination) zur Erdoberfläche und ist etwa 10° steiler als die Richtung der Zentrifugalkraft.
| Beschleunigung auf der Erdoberfläche durch Tagesrotation | |||
| Radius | R | 6 300 000 | m |
| Tag | T | 86400 | s |
| Winkelgeschwindigkeit | ω = 2 pi / T | 7.27221E-05 | 1/s |
| Geschwindigkeit |
v = ω *
R |
458.1 |
m/s |
| Zentrifugalbeschleunigung. | ω² * R | 3.33E-02 | m/s² |
| 33.3 | mm/s² |
 |
| Abb. 03-00-01: schematisch: Die Erdkugel (türkis) mit Erdachse (schwarz), Äquatorebene (gelblich), Horizont und Gebäude bei 50° nördlicher Breite (grün), Ebene bei 50° nördlicher Breite parallel zur Äquatorebene (rötlich) (FB) |
 |
| Abb. 03-00-02: Die Ebene parallel zur Erdachse (gelblich) steht senkrecht zur Richtung der Zentrifugalkraft. (FB) |
 |
| Abb. 03-00-03: Blick auf den Norpol. Ruhende Teilchen beim Gebäude werden von der Fliehkraft nach außen beschleunigt, sofern keine anderen Kräfte wirken. Sie bleiben innerhalb der roten Ebene und werden von der Corioliskraft nach rechts abgelenkt (schematisch) (FB) |
3.1 Ablenkung ohne zusätzliches elektrisches Feld, Aufspaltung durch Erdmagnetfeld oder Zentrifugalkraft?
Dipol horizontal in Ost-West-Richtung
15.04.2020
 |
| Abb. 03-01-01:
Frequenzgenerator und Meßgerät mit der
Einstellung Volt RMS Einstellung SINUS !!!!, geplant war Dreieck Vergleichsmessung s. Abb. 03-01-07 hat nur geringe Unterschiede ergeben. 15.04.2020 (FB) |
 |
| Abb. 03-01-02: die beiden
Messingstäbe haben die gleiche Orientierung
bezüglich der Ziehrichtung des Materials. (blaue
Markierung) Die "Wurzel-Seite" zeigt nach
rechts (Osten). 15.04.2020 (FB) |
 |
| Abb. 03-01-03: Blick nach
Osten. Es gibt links und rechts von der
Hauptrichtung jeweils drei Streifen mit spürbarer
Intensität, die ausgelegten Hölzer am Meßkreis
(Radius 3,5 m) markieren die Lagen der Streifen. Ausgelegt ist eine Einstellung von Frequenz und Amplitude, bei der die Ablenkung stark ist. 15.04.2020 (FB) |
 |
| Abb. 03-01-04: andere Einstellung,
die Ablenkung ist schwächer. 15.04.2020 (FB) |
 |
| Abb. 03-01-05: keine zusätzliche
elektrische Ablenkung. Zwei Frequenzen 5 Hz
und 15 Hz Dipol in Ost-West-Richtung, passend zu den beiden Abbildungen vorher. Auf beiden Seiten der Dipolachse (Ost und West) gibt es jeweils eine Struktur mit drei Sektoren. Deren Lage (Ablenkungswinkel) hängt von der Frequenz und der Amplitude ab. Ausgemessen wurde nur die östliche Seite. rot: hohe Frequenz - geringe Ablenkung, blau: niedrige Frequenz - größere Ablenkung, (die Amplituden sind nahezu gleich). Es gibt eine ähnliche Struktur am anderen Ende des Dipols, auf der Westseite. Die Qualität ist anders (komplementär?). (FB) |
 |
| Abb. 03-01-06: Blick nach Norden, der
Dipol zeigt in Richtung Ost-West. 15.04.2020 (FB) |
 |
| Abb. 03-01-07: Effektivwerte und Spitzenwerte: Sinus 3.44 Vss 9.785 Hz, 1.415 V RMS (FB) |
 |
| Abb. 03-01-08: Dreieck, 3.76
Vss 9.785 Hz, 1.440 V RMS
(FB) |
 |
| Abb. 03-01-09: keine zusätzliche
elektrische Ablenkung. Winkelposition der Streifen am Meßkreis und Frequenzen von 10 Hz, 15 Hz und 20 Hz. Unterschiedliche Frequenzen bei gleicher Signalamplitude von etwa 1.5 V Die Steigungen der Trendlinien geben an, um wieviel der Ablenkwinkel von Streifen zunimmt. 12,6°, 18.5° und 21.2° Differenz jeweils zwischen den Streifen. Je höher die Frequenz um so geringer ist der Ablenkwinkel. Die gelben Quadrate gehören zu einer Messing mit Dreieck-Signal. 1.5 V 10 Hz Dreieck verhalten sich ähnlich wie 1.5 V 15 Hz Sinus Da die Spannung als TRUE-RMS-Signal (Effektivwert) gemessen wurde und nicht als Spitz-Spitze-Signal, könnte der Unterschied an der nicht vergleichbaren Einstellung der Spannung liegen. Beim Nachmessen ergibt sich ein Unterschied von etwa 10 % für die Spannung: Dreieck: 1.46 V RMS entspricht 3,8 Vss d.h. 1.9 V (Der RMS-Wert schwankte ein wenig. )(FB) |
 |
| Abb. 03-01-10: keine zusätzliche
elektrische Ablenkung. Unterschiedliche Frequenzen bei gleicher Signalamplitude von etwa 2.5 V Je höher die Frequenz um so geringer ist der Ablenkwinkel. (FB) |
 |
| Abb. 03-01-11: keine zusätzliche
elektrische Ablenkung. Unterschiedliche Signalamplituden bei gleicher Frequenz von 20 Hz. Je höher die Amplitude um so geringer ist der Ablenkwinkel. (FB) |
 |
| ABb. 03-01-12: keine zusätzliche
elektrische Ablenkung. Zusammenfassung aus den vorherigen Darstellungen. Zunahme der Ablenkwinkel bei unterschiedlichen Frequenzen und Amplituden. Je höher die Frequenz um so geringer ist der Ablenkwinkel, je größer die Amplitude um so geringer ist der Ablenkwinkel. (FB) |
 |
| Abb. 03-01-13:keine zusätzliche
elektrische Ablenkung. bei unterschiedlichen Frequenzen: Zusammenfassung aus den vorherigen Darstellungen. Zunahme der Ablenkwinkel bei unterschiedlichen Frequenzen und Amplituden. Je höher die Frequenz um so geringer ist der Ablenkwinkel, je größer die Amplitude um so geringer ist der Ablenkwinkel. (FB) |
16.04.2020
Dipol mit Wechselspannung 10 Hz bis 160 Hz
Aufbau nicht ideal, da Dipolstäbe nicht zwingend parallel geführt
  |
| Abb. 03-01-14: Dipol senkrecht
zur Erdachse (in Richtung der
Zentrifugalkraft), es gibt wenige,
einfache spürbare Strukturen 16.04.2020
(FB) |
 |
| Abb. 03-01-15: Dipol parallel zur
Erdachse, "alles voll" , viele
spürbare Strukturen 16.04.2020 (FB) |
 |
| Abb. 03-01-16: Dipol parallel zur
Erdachse (FB) |
Dipol in Richtung Ost-West
 |
| Abb. 03-01-17: (Abb. 03-01-02)
Anordnung etwa wie diesem Foto (FB) |

xxxxxxxxxxxxxxxxxxxxxxxxx
|
| Abb. 03-01-18: schematisch: In
Längsachse gibt es auf jeder Seite zwei
Keulenorbitale. Die Ausdehnung in Längsrichtung vom inneren Orbital wurde hier bestimmt. Sie nimmt mit der Frequenz zu. (FB) |
 |
| Abb. 03-01-18: Dipol in Richtung
Ost-West. An beiden Enden des Dipols gibt es um die
Längsachse keulenförmige Strukturen. Die Reichweite der inneren Struktur (Länge) wächst mit der Frequenz, d.h. mit der Beschleunigung. Außerhalb von dieser Grenze gibt es das "Beugungsmuster" wie in Kapitel-3. ?????? (Übergang von Teilchen in Wellen?) (FB) |
30.05.2020
Dipolstäbe auf Holzleiste, daher besser ausgerichtet
3.2 Wechselspannung
Wechselspannung, Dipol horizontal in Ost-West-Richtung
verbesserte Halterung sorgt für Parallelität der Stäbe
30.05.2020
 |
| Abb. 03-02-01: Blick nach Norden,
Messing-Dipol ist horizontal in Ost-West-Richtung Wechselspannung am Dipol (FB) |
 |
| Abb. 03-02-02: Der Dipol zeigt nach
Westen. Die Verbindung bis zum Frequenzgenerator
besteht aus einem Drahtpaar (symmetrisch).
Wechselspannung am Dipol (FB) |
 |
| Abb. 03-02-03: Funktionsgenerator und
Voltmeter, der Generator wird aus einem Akku
(erdfrei) gespeist. Das zweiadrige Kabel verläuft
symmetrisch bis zum Dipol. (FB) |
 |
| Abb. 03-02-04: Blick nach Nordwesten,
Wechselspannung 0.25 VRMS am Dipol, im
Westen wurden keine Strukturen erfaßt. (FB) |
 |
| Abb. 03-02-05: Wechselspannung am
Dipol, Ost-West-Richtung, "Blick von oben", die beiden Streifen im Süden mit anderen Qualitäten sind rot markiert. (FB) |
 |
| Abb. 03-02-06: Strukturen im Süden,
Wechselspannung am Dipol, es gibt zwei
charakteristische Streifen mit anderen Qualitäten
(rot markiert). (FB) |
 |
| Abb. 03-02-07: Linker und rechter
Rand der spürbaren Streifen. Die Abstände sind ähnlich (im Osten 0.77 m ~ 13°). Die beiden rot ausgelegten Streifen (Index 11.5 und 13.5) passen nicht in dieses Schema hinein. (FB) |
 |
| Abb. 03-02-08: Dipol etwas gegen die
Horizontale geneigt, Ost-West-Richtung Wechselspannung am Dipol Bei dieser Schiefstellung sind die Strukturen nicht mehr zu finden. (FB) |
Wechselspannung, Dipol in Richtung zum Polarstern
30.05.2020
 |
| Abb. 03-02-09: noch eine andere
Möglichkeit: Dipol zeigt in Richtung Polarstern, Wechselspannung am Dipol (FB) |
 |
| Abb. 03-02-10: Blick von Osten nach Westen, Dipol zeigt in Richtung Polarstern, Wechselspannung. (FB) |
 |
| Abb. 03-02-11: Dipol in Richtung
Polarstern, Wechselspannung. Linker und rechter Rand der spürbaren Strukturen bei variabler Wechselspannung von 66 bis 263 μV. (Das ist etwa um den Faktor 1000 kleiner als bei der vorherigen Messung). Auch hier gibt es jeweils auf beiden Seiten der Ost-West-Richtung zwei Elemente. Diese rücken mit zunehmender Wechselspannung dichter an die Ost-West-Richtung heran. (F |
 |
| Abb. 03-02-12: Dipol in
Richtung Polarstern, Wechselspannung. Die spürbaren Strukturen rücken mit zunehmender Wechselspannung dichter an die Ost-West-Richtung heran. (FB) |
Wechselspannung, Dipol in Richtung der Zentrifugalkraft der Erde
30.05.2020
Wechselspannung, Stromleiter in Richtung der Zentrifugalkraft der Erde siehe kapitel-03-05
 |
| Abb. 03-02-13: Andere Ausrichtung:
Dipol zeigt in Richtung der Zentrifugalkraft, Wechselspannung am Dipol (FB) |
3.3 Gleichspannung
Gleichspannung, Dipol in Richtung Polarstern
31.05.2020
 |
| Abb. 03-03-01: Messing-Dipol zeigt in
Richtung zum Polarstern, ist 50° zur Erdoberfläche
geneigt. zwei Stäbe je 32 cm, lang 4 mm Durchmesser. Gleichspannung am Dipol (FB) |
 |
| Abb. 03-03-02: von einer USB-Ladebox
(Powerbank) und einem Spannungswandler auf 10 V geht
es über einen Spannungsteiler 1 MOhm zu 1 Ohm zum
Dipol (FB) |
 |
| ausgelegt sind jeweils zwei
Strukturen auf beiden Seiten der weißen Schnur in
Ost-West-Richtung, bei vier unterschiedlichen
Einstellungen. |
 |
| Abb. 03-03-03: Gleichspannung am
Dipol "Blick von oben" auf den Meßkreis, Messing-Dipol zeigt in Richtung zum Polarstern Bei allen vier Spannungen gibt es sowohl im Osten als auch im Westen jeweils zwei spürbare Streifen symmetrisch zur Ost-West Achse (graue Bereiche für 100 uV).
|
 |
| Abb. 03-03-04: Gleichspannung am
Dipol, Messing-Dipol zeigt in Richtung zum
Polarstern Bei allen vier Spannungen gibt es sowohl im Osten als auch im Westen jeweils zwei spürbare Streifen symmetrisch zur Ost-West- Richtung. Index 2, 1, -1, -2 (graue Bereiche für 100 uV)
|
3.4 Gleichspannung, Stromleiter in Richtung Zentrifugalkraft der Erde
felder.htm#magnetfeld
Für das Magnetfeld eines geraden unendlichen Leiters im Abstand R gilt:
B = μ0 * 1/ (2 Pi R) * I
μ0= 4 Pi 1E -7 Vs/(Am) ;
R = 3.5 m;
I= 1E-9 A;
B = 4 Pi 1E-7 Vs/(Am) / (2 Pi * 3.5 m) * 1E-9 A
B = 1E-7 / (2* 3.5) * 1E-9 = 1E-16 / 7 = 0. 143 E-16 Vs/m² = 0.143 E-16 T = 0.000 0143 pT
Bei diesem Experiment kommt heraus:
Es lassen sich Strukturen um einen Leiter bei Gleichströmen bis herunter auf 1 nA im Abstand von 3,5 m detektieren!
Rechnerisch wäre das Magnetfeld (abgeschätzt) dort etwa 0.0143E-15 T
Das Erdmagnetfeld liegt im Bereich von 50E-6 T , also etwa um den Faktor 1E12 größer!
02.06.2020
05.06.2020
 |
| Abb. 03-04-01: Eloxierte
Aluminiumstab, 4 mm Durchmesser ist 40° geneigt zur
Erdoberfläche, d.h. in Richtung der Zentrifugalkraft
bei 50° nördlicher Breite. Die Ziehrichtung (Spitze)
zeigt nach oben Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-02: Die Enden wurden mit
Schmirgelpapier aufgerauht, da die Eloxalschicht
isoliert Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-03: das untere Ende mit
aufgerauhter Oberfläche Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-04: USB-Ladebox
(Powerbank) mit Spannungsregler auf 10 V.
Nachgeschaltet ein Spannungsteiler 1000 Ohm: 100 Ohm
auf 1 V (Anzeige 0.9225) Über einen einstellbaren Vorwiderstand 10 MOhm ergibt sich ein Strom von 0.1 uA Gleichstrom durch den Stab(FB) |
 |
| Abb. 03-04-05: Bestimmung der
Inklination des Erdmagnetfeldes. Das schwarzen Rohr mit dem Magnetfeldsensor zeigt ca. 60° nach unten. In dieser Richtung ist das Feld maximal, etwa 50,1 uT. Die Holzrampe mit dem Aluminiumstab ist 40° geneigt (90° - geografische Breite) Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-06: größere Ströme,
Markierung jeweils beider Ränder eines Streifens Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-07: Ostseite im
Vordergrund, kleinere Ströme, Markierung nur
der Mitte des Streifens. Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-08:Ostseite, Markierung
nur der Mitte der Streifen Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-09: Westseite, Markierung
nur der Mitte der Streifen. Gleichstrom durch den Stab (FB) |
 |
| Abb. 03-04-10: Gleichstrom durch den
Stab "Blick von oben" auf den Meßkreis Markierung nur der Mitte der spürbaren Streifen. Richtung der spürbaren Elemente der Strukturen bei Gleichstrom von 1 nA bis 500 nA, beim Umpolen ergibt sich kein signifikanter Unterschied der Strukturen. Es gibt jeweils zwei spürbare Streifen, etwa 10 cm breit, oberhalb und unterhalb der Ost-West-Linie, einzeichnet ist deren Mittellinie. Die hellblauen Formen kennzeichnen die Positionen für 100 nA. Mit abnehmendem Strom rücken sie an die Mittellinie heran (Pfeile). Weicht die Richtung des Dipols einige Grad davon ab, dann gibt es diese Strukturen nicht. (FB) |
 |
| Abb. 03-04-11: Ausschnitt (FB) |
 |
| Abb. 03-04-12: Gleichstrom durch den
Stab Markierung nur der Mitte der spürbaren Streifen. Bei dieser Art der Auftragung läßt sich feststellen, ob die Winkel der äußere Elemente ein Vielfaches der Winkel von den inneren sind. Die hellblauen Flächen zeigen bei 100 nA die Lage von jeweils vier Streifen im Westen wie im Osten an. Die hellblauen Formen kennzeichnen die Positionen für 100 nA. Bei 100 nA (blau) verdoppelt sich der Winkel jeweils. Die gestrichelten Linien gehören zu einer Wiederholungsmessung für 100 nA drei Tage später. Im Rahmen der Meßgenauigkeit bestätigen sie die früher Messung. (FB) |
 |
| Abb. 03-04-13: Gleichstrom durch den
Stab noch höhere Ströme (bis 2000 nA) und unterschiedliche Polaritäten + / - 1 μA und + / - 2 μA, Bei noch höheren Strömen 5 μA, 10 μA und 20 μA steigt die Anzahl der Elemente weiter an. Bei 20 μA ist es unübersichtlich und etwa dreiviertel des Meßkreises ist damit angefüllt. Die hellblauen Formen zeigen bei 1000 nA die Lage von jeweils sechs Streifen im Westen wie im Osten und einen in der Mitte an. (FB) |
3.5 Wechselspannung, Stromleiter in Richtung Zentrifugalkraft der Erde
08.06.2020
 |
| Abb. 03-05-01: Exakt in Richtung der
Zentrifugalkraft der Erde ist ein 4 mm Aluminiumstab
ausgerichtet, 1000 mm lang, eloxiert und an den
Enden zum Kontaktieren angeschliffen. Die
Ziehrichtung ( Spitze) zeigt nach oben. Die
Stromzuführungen sind symmetrisch (zweiadriges
ungeschirmtes Kabel). Der ganze Stromkreis ist
erdfrei. (FB) |
 |
| Abb. 03-05-02: Aus einem 12V Akku
wird der Frequenzgenerator versorgt. Seine Ausgangsspannung (Sinus) wird mit 1000 Ohm zu 10 Ohm heruntergeteilt auf 0.1 V RMS (Voltmeter rechts oben). Aus dieser Spannung wird der Stromleiter über einen variablen Vorwiderstand (gelber Kasten) versorgt. Bei größeren Strömen läßt sich der Wert am Meßgerät rechts ablesen. Bei kleineren Strömen ( z.B. 1 nA ) ergibt sich der Wert aus der Größe des Vorwiderstandes. (FB) |
 |
| Abb. 03-05-03: Am Meßkreis mit Radius
3,6 m sind die Strukturen mit Hölzern und Häringen
ausgelegt. Mit einer Kamera auf einer ausziehbaren
Nivellierlatte läßt sich ein Übersichtsbild
erstellen. (FB) |
 |
| Abb. 03-05-04: Übersichtsbild aus 5 m
Höhe. Blick nach Westen. Der Stromleiter befindet sich etwas rechts von der Mitte des Meßkreises. Bei speziellen Frequenzen findet man Eigenschaften wie bei einem resonanzfähigen System. Es gibt spürbare Strukturen, wenn die Frequenz 13.6 Hz oder im Bereich eines Vielfachen davon ist. z.B. bei 13.6 Hz ist die Intensität stark, außerhalb davon wird sie schwächer und bei 12.5 Hz bzw. 15.0 Hz gibt es keine Strukturen. Es scheinen die gleichen Frequenzen wie bei dem "Resonanzrohr" ( Abb. xx, Kapitel 7) zu sein. Die weiße Schnur zeigt die Ost-West-Richtung an, ausgelegt sind Markierungen für Wechselstrom bei den Frequenzen 13.6 Hz (grüne Hölzer) und 25.9 Hz (rote Häringe). Auf beiden Seiten der Schnur gibt es jeweils 4 bzw. 8 spürbare Elemente. (FB) |
|
|
| Abb. 03-05-05: "Blick von oben" |
 |
| Abb. 03-05-06: Zählt man die
Strukturen der Reihe nach durch und trägt deren
Positionen über der fortlaufenden Nummer auf,
ergeben sich Geraden für 13.6 Hz und 25.9 Hz. Die Steigung der Geraden ist etwa gleich, wenn die 25.9 Hz-Daten mit halbzahligen Index aufgetragen werden. d.h. die Steigung bei ganzzahliger Auftragung wäre halb so groß. Aus den jeweils durchgezogenen und gestrichelten Linien läßt sich die Breite der Strukturen erkennen. Die roten Elemente sind schmaler als die blauen. Die Kurven sind etwas unsymmetrisch zur Ost-West-Linie, vermutlich weil der Stromleiter etwas nördlicher vom Mittelpunkt des Kreises ist. (FB) |
 |
| Abb. 03-05-07: Alu-Stab 4 mm,
Alu-Stab 5 mm, Gewindestange Messing 8 mm, Gewindestange verz. Eisen 8 mm, 4-kant Eisen 4 mm Messingrohr 5 mm Kupferstab 6 mm, Stahlstab 4 mm und 8 mm |
 |
| Abb. 03-05-07: Hölzer (grün): Alu-Stab 4 mm, Alu-Stab 5 mm, Gewindestange Messing 8 mm, Gewindestange verz. Eisen 8 mm, 4-kant Eisen 4 mm Messingrohr 5 mm Häringe (rot): Kupferstab 6 mm, Stahlstab 4 mm und 8 mm (FB) |
4. Einfluß der Erdachse auf andere Objekte
4.2 Helmholtz-Spule
 |
| Abb. 04-02-00: Helmholtzspule,
Wicklung aus seidenumsponnenem Kupferdraht, Ausrichtung senkrecht zur Erdachse (FB) |
 |
| Abb. 04-02-00a: Erdachse und
Äquatorebene. (FB) |
 |
| Abb. 04-02-01: Gleichstromquelle für
PicoAmpere Spannungsteiler 1:1000,
Vorwiderstand 10 MOhm Der Innenleiter vom BNC-Kabel ist der Pluspol (rot), Minuspol (blaus) Eingestellte Ströme: 114 pA, 50 pA, 25 pA, 14 pA (+/- 5 pA Schwankung) (FB) |
 |
| Abb. 04-02-02: Helmholtzspule mit
seidenumsponnenen Kupferdraht, Spulenachse zeigt senkrecht zur Erdachse, nahezu Nord-Süd-Richtung Neigungswinkel ca. 49 °, geografische Breite des Ortes (FB) |
 |
| Abb. 05-02-03: nahezu
Nord-Süd-Richtung (FB) |
 |
| Abb. 04-02-04: Der rote Draht
(Pluspol) geht nach oben (CCW), der
andere nach unten (Pfeil, CW) (FB) |
 |
| Abb. 04-02-05: Wichtig:
Wasserwaage und Schnur für die Ausrichtung Nord-Süd
Noch Forschungsbedarf: hier nicht die exakte Nordrichtung, Schnur zeigt etwa 5° nach NordOst , Spulenhälften nicht parallel usw. (FB) |
 |
| Abb. 04-02-06: schematisch,
Spulenachse in Nord-Südrichtung (im Bild oben-unten) An jedem Ende gibt es in Achsenrichtung mehrere räumliche Objekte. In der Mitte ist eine eingebeulte Keule (sehr viel kleiner als die Schalen in dieser Zeichnung), weiter zur Seite schließen sich zwei schalenförmige Gebilde an. Nord- und Südseite unterscheiden sich in der Größe. Berechnet für spherical harmonics , mit Programm von R. Matzdorf, Universität Kassel http://www.uni-kassel.de/fb10/institute/physik/forschungsgruppen/oberflaechenphysik/quantum-analogs/sperical-harmonics.html (FB) |
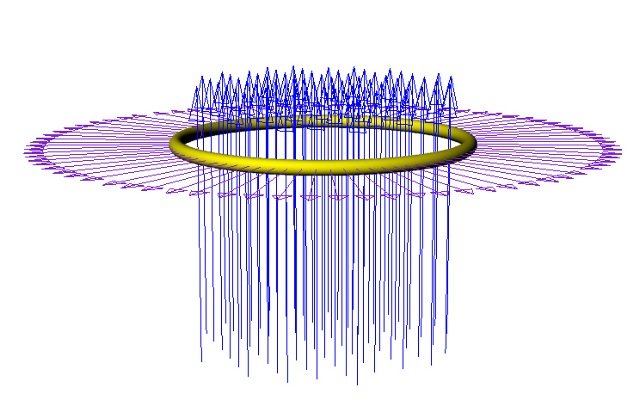 |
| Abb. 04-02-07: Wenn durch den gelben
Ring ein Gleichstrom fließt, wirkt auf die
Ladungsträger eine Zentrifugalkraft (lila Pfeile)
nach außen. Bei exakter Anordnung steht die
Zentrifugalkraft durch die Rotation der Erde (blaue
Pfeile) senkrecht dazu. (FB) |
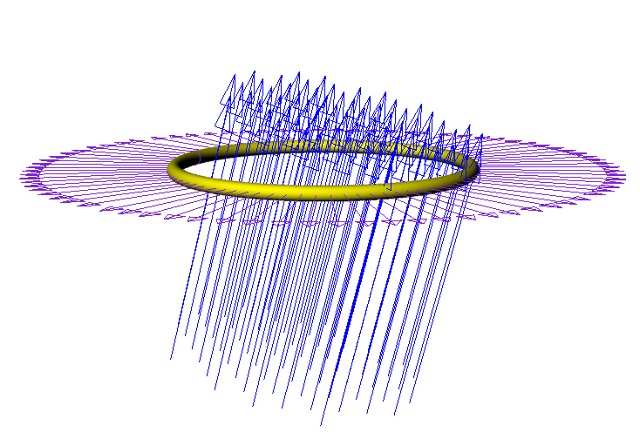 |
| Abb. 04-02-08: Ist der Ring nicht
orthogonal, dann gibt es Unsymmetrien, die zu
Wirbeln führen können (FB) |
Bei exakter Orientierung (Spulenachse zeigt senkrecht auf die Erdachse ) sind die Strukturen auf der Südseite klein.
Schon bei einigen Grad Abweichung von dieser Richtung wachsen die Strukturen an. Ihre Intensität nimmt zu.
Bei umgekehrter Polung werden die Strukturen intensiv ( auf der Südseite unangenehm)
Bei 114 pA gilt für die Polung plus bei der Südseite: Länge von Keule: 0.4 m, Schale 1 : ca. 1 m, Schale 2: ca. 1.5 m
Nordseite: einige Meter
bei Polung minus: Südseite Strukturen im Bereich von einigen Metern.
Bei kleineren Strömen schrumpfen die Strukturen entsprechend proportional.
noch Forschungsbedarf!
4.3 Spule mit Lichtleiter
Bei Beleuchtung eines Faserendes mit Sonnenlicht entstehen ähnliche Strukturen wie bei der Helmholtzspule.
Sie unterscheiden sich allerdings in der Anzahl d.h. es gibt nicht 3 sondern erheblich mehr ( 9?) Elemente.
Bei einer Entfernung zur Spule entlang der Achse um ca. 5 m, sind die "Schalen" etwa 1 m dicht auseinander.
 |
| Abb. 04-03-01: Spule mit
Lichtleiter. Das eine Ende ist mit einer
lichtundurchlässigen Kappe verschlossen. Das andere
Ende hängt am oberen Rand. Es ist dem Sonnenlicht
ausgesetzt (FB) |
 |
| Abb. 04-03-02: Die Spule ist etwa 49°
gegen den Horizont (geografische Breite) geneigt. Das Sonnenlicht scheint auf das Ende der Faser. (FB) |
 |
| Abb. 04-03-03: Mit Hilfe der Zwinge
läßt sich das Faserende bequem zur Richtung der
Sonne ausrichten. Sofern das Ende beleuchtet wird, gibt es ähnliche Strukturen wie bei der Helmholtz-Spule. Je nach Fehlstellung zur Richtung der Sonne kann die eingestrahlte Intensität variiert werden. Deckt man es wie hier mit einem Schattengeber ab, verschwinden die Strukturen. Sie kommen sofort wieder, wenn man den Schattengeber entfernt. (FB) |
 |
| Abb. 04-03-04: Faserende im Schatten
(FB) |
5. Beugung
Zusammenfassung
Bei den Experimenten zeigt sich, daß die Richtung senkrecht zur Rotationsachse der Erde eine besondere Rolle spielt.
Es ist die Richtung der Fliehkraft der Erdrotation.
bewegte-materie-oszillierend.htm#kapitel-10-02
Die Erdbeschleunigung ist 9,81 m/s² und daher etwa um den Faktor 300 größer.
Mit der üblichen Annahme, daß schwere Masse zahlenmäßig gleich der trägen Masse ist, d.h. die beiden Größen nicht unterscheidbar sind, kommt man hier nicht weiter. Es dürfte keine Wirkung geben, weil die Erdanziehung die Zentrifugaleffekte überwiegt.
Wenn nun aber doch Effekte in Richtung der Zentrifugalkraft auftreten, dann folgt daraus, daß hier Teilchen beteiligt sind, die überwiegend träge Masse haben.
Damit es Beugungseffekte geben kann, müssen die Teilchen Wellen erzeugen.
Vermutlich geschieht dies, wenn sie auf Materie wie z.B. das Drahtgitter treffen.
 |
| Abb. 05-01-01a: Das "Beugungsmuster" ist symmetrisch zur roten Ebene (parallel zur Äquatorebene) (FB) |
kapitel-05-01
 |
| Abb. 05-01-07a: Neigungswinkel des Gitters, Rotation um horizontale Achse. |
 |
| Abb. 05-01-09: Die beobachteten
Strukturen bei unterschiedlichen Neigungswinkeln. von rechts nach links 51.6; 51.1; 50.6; 50.1; 49.6; 49.1; 48.6; 48.1; 47.6; 47.1 ° Zwischen 49° und 50° gibt es ein Minimum der Ablenkung. Der Winkel entspricht der geografischen Breite des Ortes. (FB) |
kapitel-05-06-02
 |
| Abb. 05-06-08: Die Ebene des Gitters
steht parallel zur Erdachse, Rotation um lotrechte Achse (FB) |
 |
| Abb. 05-06-13: von links nach rechts: -15°, -10°, -5°, 0°, 0°, 5°, 10° und 15° (FB) |
 |
| Abb. 05-06-15: Aus den Steigungen ermittelt: Der Abstand zwischen jeweils zwei Maxima verringert sich fast um den Faktor 2, wenn das Gitter aus der Nord-Süd-Richtung herausgedreht wird. (FB) |
kapitel-05-06-01
 |
| Abb. 05-06-02: Drehung um eine lotrechte Achse, z.B. 20° (FB) |
 |
| Abb. 05-06-06: Aus den Steigungen der
vorherigen Grafik ermittelt. Der Abstand zwischen jeweils zwei Maxima vergrößert sich, wenn der Aluminium-Stab aus der Nord-Süd-Richtung herausgedreht wird. (FB) |
5.1 Beugung am Drahtgitter
 |
| Abb. 05-01-01: Probeaufbau. Ein Drahtgitter (Pellkartoffelschneider) liegt auf dem Pult, links oben ist eine Halterung für einen "Projektionsschirm" zur Aufnahme eines "Beugungsmusters". (FB) |
 |
| Abb. 05-01-01a: Das "Beugungsmuster"
ist symmetrisch zur roten Ebene (parallel zur
Äquatorebene) (FB) |
 |
| Abb. 05-01-02: Ein Blatt Papier zum
Aufzeichnen der Beugungsmuster (FB) |
 |
| Abb. 05-01-03: verbesserte Version:
M10-Gewinde mit Flügelmutter zur Verstellung der
Neigung sowie ein Neigungsmesser mit elektronischer
Anzeige auf dem Pult. Zum Aufzeichnen der Muster dient ein Pappkarton mit zwei DINA-4 Papieren darauf. Abstand vom Gitter bis zur Projektionsebene: 550 mm. (FB) |
 |
| Abb. 05-01-04: Neigungsmesser,
Anzeige 51.0°, Auflösung 1/10°, dahinter das
Drahtgitter Dreht man das Gerät um 180°, dann ist die Anzeige bei 51.4°, d.h. der Winkelfehler ist 0.4/2 = 0.2° (FB) |
 |
| Abb. 05-01-05: Das Drahtgitter hat 20
Drähte auf 96 mm. d.h. Abstand 5.05 mm, Drahtstärke
0.30 mm (FB) |
 |
| Abb. 05-01-06: Die Drähte sind in
einem Aluminium-Rahmen eingespannt. (FB) |
 |
| Abb. 05-01-07: Die Neigung läßt sich
mit der Gewindestange verändern. ausgenutzter Verstellbereich + / - 3° (FB) |
 |
| Abb. 05-01-07a: Neigungswinkel des
Gitters. Rotation um horizontale Achse. (Fb) |
 |
| Abb. 05-01-08: Die beobachteten
Strukturen bei unterschiedlichen Neigungswinkeln. von oben nach unten 51.6; 51.1; 50.6; 50.1; 49.6; 49.1; 48.6; 48.1; 47.6; 47.1 ° Es gibt etwa alle 5 cm eine höhere spürbare Intensität. Bei Durchgang von oben nach unten verschieben sich die Muster zunächst nach rechts. Bei etwa 49.5° kehrt sich das Vorzeichen der Verschiebung um. (FB) |
 |
| Abb. 05-01-09: Die beobachteten
Strukturen bei unterschiedlichen Neigungswinkeln. von rechts nach links 51.6; 51.1; 50.6; 50.1; 49.6; 49.1; 48.6; 48.1; 47.6; 47.1 ° Zwischen 49° und 50° gibt es ein Minimum der Ablenkung. Der Winkel entspricht der geografischen Breite des Ortes. (FB) |
 |
| Abb. 05-01-10: Beugungswinkel bei
unterschiedlichen Neigungswinkeln. Die Maxima werden
der Reihe nach durchgezählt. Mittelstellung beim
Index = 0 Der Abstand der Maxima beträt etwa 5.7°. Mit zunehmendem Abstand des Neigungswinkels von 49.6° wandern die Beugungswinkel im Diagrammnach oben. (Die Markierungen auf dem Projektionsschirm haben sich nach links verschoben.) (FB) |
 |
| Abb. 05-01-11: Für die mittlere der
Kurvenschar beim Neigungswinkel 49.6° (geografische
Breite) läßt sich eine Wellenlänge von etwa 0.5
mm mit der Gleichung n*lambda = d
* sin(alpha) ausrechnen. Für die Kurven bei anderen Neigungswinkeln gibt es Abweichungen besonders im Bereich der Mitte, denn das "nullte" Maximum liegt nicht in der Mitte. (FB) |
Weitere Beobachtungen
Haushaltsfolie und Drahtgitter
Die Intensität ist verringert. Dabei spielt die Ausrichtung horizontal, vertikal keine Rolle.ausbreitung.htm
/Reddish 2010/ Seite IX und XV
"If the interferometer is shielded from the sun by aluminium foil or crossed sheets of stretched polyethylene film, the pattern disappears.
About this time an article by two Russian authors, Nachalov and Parkhomov, appeared on the Internet reporting that stretched polyethylene film (commonly used as 'clingfilm' in Britain for wrapping food) polarises torsion radiation, a comprehensive term used by them and their colleagues that supposedly includes fields produced by rotating masses.
This seemed to me then to be a remarkable discovery, and still does. I was sufficiently suspicious to want to confirm it and that was easily done by polarising the field by reflection with aluminium and cross-polarising by transmission through stretched polyethylene film, which eliminated the field (having first established that the film transmitted the unpolarised field)."
Gestrecktes Polyethylen polarisiert die Strahlung von rotierenden Körpern. Reddish hat diese Aussage von zwei russischen Autoren Nachalov und Parkhomov mit an Aluminium reflektierter Strahlung bestätigen können.
Yu.V.Nachalov, E.A.Parkhomov. Experimental detection of the torsion field. http://www.amasci.com/freenrg/tors/doc15.html
 |
| Abb. 05-01-12: Drahtgitter und
Haushaltsfolie (FB) |
5.2 Beugung an Loch und Scheibe
 |
| Abb. 05-02-01: Eine leicht
elliptische Scheibe aus Aluminiumfolie erzeugt ein
ringförmiges "Beugungsbild". Die matte Seite
muß zum Projektionsschirm zeigen. (FB) |
 |
| Abb. 05-02-02: Auch bei der Folie mit
dem Loch gibt es ein ähnliches Muster. Babinet'sche
Theorem, Das gestanzte Aluminiumblech erzeugt ein zweidimensionlases Muster. (FB) |
 |
| Abb. 05-02-03: Scheiben aus
Aluminiumfolie mit unterschiedlichen Durchmessern,
Blick auf die matte Seite. (FB) |
 |
| Abb. 05-02-04: Aufbau zum Ausmessen
der Beugungsbilder bei Scheiben mit
unterschiedlichen Durchmessern (FB) |
 |
| Abb. 05-02-05: Der Satz der
Aluminiumscheiben auf dem Lochblech. (FB) |
 |
| Abb. 05-02-06: Die von dem Papier
abgenommenen Maße für die unterschiedlichen Scheiben
aus Alufolie, jeweils Anfang und Ende einer Struktur
(FB) |
 |
| Abb. 05-02-07: Schematisch, aus den
Meßpunkten konstruierte Kreisringe rot: große Scheibe, 65mm; blau: 55 mm; grau: kleine Scheibe 28 mm (FB) |
5.3 Beugung an Stäben
 |
| Abb. 05-03-01: Zwei Titanbleche mit
einer Lücke dazwischen erzeugen eine "Beugungsbild".
(FB) |
 |
| Abb. 05-03-02: Zwei Eisenstäbe,
parallel zueinander, erzeugen ein "Beugungsbild" Abstand 105 mm (FB) |
 |
| Abb. 05-03-03: Abstand 56 mm (FB) |
 |
| Abb. 05-03-04: Abstand 189 mm (FB) |
 |
| Abb. 05-03-05: vierter Versuch mit
Aluminium-Stäben, Abstand 56 mm (FB) |
5.4 Beugung beim Doppelspalt
Überlagerung von Kreiswellen von zwei unterschiedlichen Mittelpunkten
aus ueberlagerung.htm
 |
 |
| Abstand der Mittelpunkte:
5 Einheiten, 3 helle Streifen |
Abstand der Mittelpunkte:
7 Einheiten 5 helle Streifen |
 |
 |
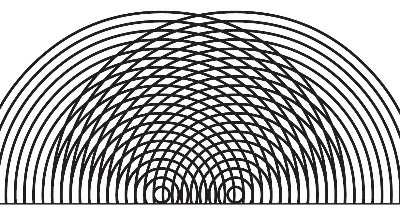
| Abstand der Mittelpunkte:
10 Einheiten 7 helle Streifen |
Abstand der Mittelpunkte:
15 Einheiten 11 helle Streifen |
 |
|
| Abstand der Mittelpunkte: 20
Einheiten 15 helle Streifen |
|
| Abb. 05-04-01a bis 01e: Konstruktive
Überlagerung von zwei Systemen konzentrischer
Kreise. Die Mittelpunkte haben jeweils
unterschiedliche Abstände. Dort wo sich zwei Kreise
exakt treffen, ist es heller und an anderen Stellen
dunkler. Ringabstand: 5 Einheiten, |
Je größer der Abstand
der Mittelpunkte wird, je kleiner ist der
Winkelabstand der Streifen. |
 |
| Abb. 05-04-02: Kreiswellen auf einer
Wasseroberfläche. Links oben ist ein luftdichtes Lautsprechergehäuse, an dessen Innenraum ein Schlauch angeschlossen ist. Bei der Bewegung der Membrane strömt Luft durch den Schlauch bis zu den beiden Düsen aus Glasrohr über der Wasseroberfläche. Der Lautsprecher wird von einem Frequenzgenerator angeregt. Damit werden periodisch Luftstöße erzeugt, die auf die Wasseroberfläche treffen und dort Wellen machen. Über der Wasserwanne ist eine punktförmige Lichtquelle. Sie zeichnet unten auf dem weißen Papier das Schattenbild dieser Wellen. Der Abstand der beiden Düsen ist verstellbar. (FB) |
 |
| Abb. 05-04-02a: Die Anreger haben etwa 8 Wellenlängen Abstand. (FB) |
 |
| Abb. 05-04-03: Die Anreger haben etwa
14 Wellenlängen Abstand (FB) |
 |
| Abb. 05-04-04: Die Anreger haben etwa 20 Wellenlängen Abstand (FB) |
 |
| Abb. 05-04-05: Schnittpunke von zwei
konzentrischen Kreisscharen. Die Mittelpunkte der Kreise haben einen Abstand von 56 mm. Die Radien der Kreise steigen mit 20 mm an. Bei Beugungsexperimente entspräche dies der Wellenlänge. Es gibt links und rechts von der Mitte jeweils zwei Richtungen, in denen die Kreisscharen Schnittpunkte haben. Beim Abstand des Projektionsschirmes in 550 mm treffen die Kurven mit den Schnittpunkten diesen Schirm etwa bei 600 mm, 210 mm, 0 mm von der Mitte aus gerechnet. Die jeweilige Steigung ist: 2.62 0.99 (FB) |
 |
| Abb. 05-04-06: Die Mittelpunkte der
Kreise haben einen Abstand von 86 mm. Schnittpunkte auf dem Projektionsschirm sind ca. 600 mm, 300 mm, 130 mm, 0 mm von der Mitte entfernt. Die jeweilige Steigung ist 1.91, 1.04, 0.25 (FB) |
 |
| Abb. 05-04-07: Die Mittelpunkte der
Kreise haben einen Abstand von 105 mm. Schnittpunkte auf dem Projektionsschirm sind ca. 410 mm, 230 mm, 110 mm, 0 mm von der Mitte entfernt. Die jeweilige Steigung ist 5.15, 2.43, 1.45, 0.88 Im unteren Bereich liegen einige Punkte nicht mehr auf der Ausgleichsgeraden. (FB) |
 |
| Abb. 05-04-08: Die Mittelpunkte der
Kreise haben einen Abstand von 141 mm. Schnittpunkte auf dem Projektionsschirm sind ca. 415 mm, 270 mm, 170 mm, 80 mm, 0 mm von der Mitte entfernt. Die jeweilige Steigung ist 6.98, 3.38, 2.14, 1.47, 1.04, 0.64 Im unteren Bereich liegen einige Punkte nicht mehr auf der Ausgleichsgeraden. (FB) |
 |
| Abb. 05-04-09: Die Mittelpunkte der
Kreise haben einen Abstand von 189 mm. Schnittpunkte auf dem Projektionsschirm sind ca. 520 mm, 380 mm, 280 mm, 195 mm, 120 mm, 55 mm ,0 mm von der Mitte entfernt. Die jeweilige Steigung ist 9.4, 4.62, 2.99, 2.15, 1.62, 1.26 Im unteren Bereich liegen einige Punkte nicht mehr auf der Ausgleichsgeraden. (FB) |
 |
| Abb. 05-04-09a:Mit den
"Beugungswinkeln" der Kreisscharen über einer
fortlaufenden Zahl aufgetragen. (FB) |
 |
| Abb. 05-04-09b: Probe aufs Exempel: Aus den "Beugungswinkeln" der Kreisscharen errechnete Wellenlänge. Die Wellenlänge liegt im Bereich 20 +/- 1 mm Die für die Rechnung benutzten Kreisscharen haben einen Abstand von 20 mm. (FB) |
doppelspalt.htm
Das Babinet’sche Prinzip (auch Babinet’sches Theorem) besagt, daß die Beugungsbilder zweier zueinander komplementärer Blenden (beispielsweise Spaltblende und ein Draht gleicher Dicke) sich nicht unterscheiden.
https://de.wikipedia.org/wiki/Babinetsches_Prinzip
Im Folgenden geht es um das Beugungsbild von zwei zueinander parallelen Stäben, gerechnet wurde aber die Intensität für zwei Spalte gleicher Anordnung.
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 05-04-10: Intensität bei einem
Doppelspalt aufgetragen gegen die Position auf dem
Schirm, Spaltbreite 6 mm, Spaltabstand 189
mm, Wellenlänge 20 mm und Abstand bis zum Schirm 550 mm Formel S. 894, Physics for Scientists & Engineers with Modern Physics D.C. Giancoli, Rechnung für monochromatische Strahlung für sehr großen Abstand der Projektionsfläche im Vergleich zur Wellenlänge (zutreffend ??)
aus der Rechnung für die Positionen der Maxima: -451, -342, -256, -184, -118, -58.7, 0, 58.7, 118, 184, 256, 342, 451 mm Die Breite der Öffnung der beiden Spalte spielt für das Ergebnis nur eine vernachlässigbare Rolle. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| bb. 05-04-11: Intensität bei einem
Doppelspalt, Spaltbreite 6 mm, Spaltabstand 105 mm, Wellenlänge 20 mm und Abstand bis zum Schirm 550 mm |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 05-04-11a: Intensität bei einem
Doppelspalt, Spaltbreite 6 mm, Spaltabstand 105 mm, Wellenlänge 17 mm und Abstand bis zum Schirm 550 mm Wellenlänge geringfügig geändert, damit das Ergebnis in den nachfolgenden Grafiken unterscheidbar ist. Position der Maxima: -466, -306, -188, 0 188, 306, 466 mm (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 05-04-12: Intensität bei einem
Doppelspalt, Spaltbreite 6 mm, Spaltabstand 56 mm, Wellenlänge 20 mm und Abstand bis zum Schirm 550 mm Wellenlänge geringfügig geändert, damit das Ergebnis in den nachfolgenden Grafiken unterscheidbar ist. Position der Maxima: -504, -198, 0, 198, 504 mm (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 05-04-13: Intensität bei einem
Doppelspalt, die geringfügig unterschiedlichen
Wellenlängen spielen kaum eine Rolle, dagegen der
unterschiedliche Abstand der beiden Spalte
(FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 05-04-14: Intensität bei einem
Doppelspalt. Die in die Rechnung eingesetzte Wellenlänge kommt bei dieser Darstellung wieder heraus. Wellenlänge wurde geringfügig unterschiedlich gewählt, damit besser unterscheidbar in der Grafik. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||
Auswertung von Beugungsbildern, Auftragung der Positionen über einer fortlaufenden Zahl
gitterbeugung.htm
 |
| Abb. 05-04-15: Beugungsbild an einem
Spalt (FB) |
 |
| Abb. 05-04-16: Aufgetragen ist die
Position der Maxima auf dem vorherigen Foto gegen
eine fortlaufende Zahl. Diese Grafik erlaubt mit einem schnellen Blick einen groben mathematischen Zusammenhang abzuleiten, bzw. Abweichungen von dem theroretisch zu erwartendem Verlauf zu finden. Folgen die Positionen in regelmäßigem Abständen aufeinander, dann ergibt sich eine Gerade. In diesem speziellen Fall gibt es offensichtlich Unterschiede links und rechts vom Index 13. Das ist die Richtung der Hauptstrahls. Aus der Steigung der Geraden lassen sich eine der Kenngrößen wie Wellenlänge, Spaltbreite, Periode oder Abstand der Beugungsobjekte ermitteln, wenn die übrigen bekannt sind. Die Steigung unterhalb von 13 ist 97.8 Pixel/Index. Die Reihe der Punkte ist geringfügig nach unten gekrümmt. Oberhalb von 13 ist die Steigung 84.1 Pixel/Index. Vermutlich stand der Schirm nicht exakt senkrecht zur Strahlrichtung. (FB) |
5.5 Beugung an zwei Stäben
 |
| Abb. 05-05-01: erster Versuch, mit Eisenstäben.
(FB) |
 |
| Abb. 05-05-02: zweiter Versuch, mit Eisenstäben
(FB) |
 |
| Abb. 05-05-03: dritter Versuch,
mit Aluminium-Stäben (FB) |
 |
| Abb. 05-05-04: vier Stäbe aus
unterschiedlichen Materialien, Abstand 56 mm,
Beobachter GE Position (FB) |
 |
| Abb. 05-05-05: vier Stäbe aus unterschiedlichen
Materialien, Abstand 56 mm, Beobachter GE Winkel (FB |
 |
| Abb. 05-05-06: vier Stäbe aus unterschiedlichen
Materialien, Abstand 56 mm, Beobachter GE (FB) |
 |
| Abb. 05-05-07: vierter Versuch,
mit Aluminium-Stäben (FB) |
 |
| Abb. 05-05-08: vierter Versuch mit Aluminium-Stäben,
Versuch zur Bestimmung einer Wellenlänge Die Gleichung d * sin(alpha) = n * lambda scheint näherungsweise zu passen --> Wellenlänge 15-25 mm Allerdings könnten bei den inneren Maxima die Indizes etwa anders sein. Möglicherweise ist der Schirm bei diesen großen Abständen der Stäbe zu dicht dran. Auch die gerechneten Daten (Gciancoli) für d= 56, d= 105 und d= 189 mm sind dabei. (FB) |
 |
| Abb. 05-05-09:
unterschiedliche Materialien, Abstand der Stäbe 56
mm Versuch zur Bestimmung einer Wellenlänge Die Gleichung d * sin(alpha) = n * lambda scheint zu passen --> Wellenlänge 10-20 mm (FB) |
 |
| Abb. 05-05-10: dritter Versuch,
Aluminiumstäbe Versuch zur Bestimmung einer Wellenlänge d * sin(alpha) = n * lambda näherungsweise passend (FB) |
 |
| Abb. 05-05-11: allererster
Versuch mit Eisenstäben Versuch zur Bestimmung einer Wellenlänge d * sin(alpha) = n * lambda näherungsweise passend (FB) |
 |
| Abb. 05-05-12: zweiter Versuch
mit Eisenstäben , große Fehler ?? Versuch zur Bestimmung einer Wellenlänge wird kaum erfüllt: d * sin(alpha) = n * lambda (FB) |
5.6 Einfluß der Orientierung bezüglich einer lotrechten Achse
5.6.1 Leichte Verdrehung um lotrechte Achse, Beugung an einem Aluminium-Stab
 |
| Abb. 05-06-01: In der Halterung auf
dem Pult liegt ein 6 mm Aluminium-Stab. Die weiße Schnur zeigt exakt die Ost-West-Richtung an. (FB) |
 |
| Abb. 05-06-02: Drehung um eine
lotrechte Achse, z.B. 20° (FB) |
 |
| Abb. 05-06-03: Der Aufbau ist um +30°
um eine senkrechte Achse verdreht. Alu-Stab und Projektionsrichtung mit Maßstab haben sich mitgedreht. (FB) |
 |
| Abb. 05-06-04: Verdrehung um -30°
(FB) |
 |
| Abb. 05-06-05:Für die
Verdrehungswinkel, (blau) 0 ; 0 ; 0, (rot) +10; +20; +30; (lila) -10; -20; und -30° wurden die Postitionen einiger Beugunsmaxima ermittelt. Die Indizes der lila und roten Kurven wurden jeweils gruppenweise um +1 bzw. -1 verschoben, damit die Kurven sich nicht überdecken. Bei den lila und roten Kurven zeigt sich ein Anstieg der Steigung mit zunehmendem Verdrehungswinkel. Bei den blauen Kurven gibt es eine geringe Änderung von Messung zu Messung. Es gab eine leichte Verschiebung mit der Zeit. Es scheint eine ständige Verschiebung des "Nullpunktes" zu geben, periodisch im Bereich von einigen Minuten? (FB) |
 |
| Abb. 05-06-06: Aus den Steigungen der
vorherigen Grafik ermittelt. Der Abstand zwischen jeweils zwei Maxima vergrößert sich, wenn der Aluminium-Stab aus der Nord-Süd-Richtung herausgedreht wird. (FB) |
5.6.2 Leichte Verdrehung um lotrechte Achse, Beugung an einem Drahtgitter
 |
| Abb. 05-06-07: Das Drahtgitter
(Pellkartoffelschneider) rotiert um eine vertikale
Achse. Seine Neigung ist 49.6 ° (FB) |
 |
| Abb. 05-06-08: Die Ebene des Gitters
steht parallel zur Erdachse, Rotation um lotrechte Achse (FB) |
 |
| Abb. 05-06-09: Blick nach Süden, auf
der Pappe sind die Positionen für -15°, -10°, -5°, 0°, 0°, 5°, 10° und 15° markiert. (FB) |
 |
| Abb. 05-06-10: Abstand zur Pappe: 70
cm (FB) |
 |
| Abb. 05-06-11: von oben nach
unten: -15°, -10°, -5°, 0°, 0°, 5°, 10°, 15° weiß, grün, rosa, blau blau rosa, grün, weiß Die Positionensangaben in mm wurden anschließend auf die Pappe geschrieben.(FB) |
 |
| Abb. 05-06-12: Ausschnitt, Bild um
90° gedreht, Bereich in der Mitte, von links nach rechts: -15°, -10°, -5°, 0°, 0°, 5°, 10°, 15° weiß, grün, rosa, blau, blau rosa, grün, weiß (FB) |
 |
| Abb. 05-06-13: von links nach rechts: -15°, -10°, -5°, 0°, 0°, 5°, 10° und 15° (FB) |
 |
| Abb. 05-06-14: Positionen der Maxima
in Winkel umgerechnet. Die Verbindungskurven lassen
sich mit Geraden beschreiben. Die zugehörigen
Steigungen d.h. Differenzwinkel zwischen
jeweils zwei Maxima sind ausgegeben. (FB) |
 |
| Abb. 05-06-15: Aus den Steigungen
ermittelt: Der Abstand zwischen jeweils zwei Maxima
verringert sich fast um den Faktor 2,
wenn das Gitter aus der Nord-Süd-Richtung
herausgedreht wird. (FB) |
5.7 Beugung an einem Stab, unterschiedliche Materialien
5.7.1 Ablesung direkt während der Beobachtung
 |
| Abb. 05-07-01-01: Unterschiedliches
Rundmaterial: Messing, Aluminium, Stahl (FB) |
 |
| Abb. 05-07-01-02: auch
Aluminium-Rohre (FB) |
 |
| Abb. 05-07-01-03: kurze Stäbe aus
Blei, Zink, Nickel, Kupfer, Graphit (FB) |
 |
| Abb. 05-07-01-04: Vierkantmaterial,
Buchenholz, einfacher Stahl und Messing und dünner
Stahldraht (FB) |
 |
| Abb. 05-07-01-05: Plexiglas-Stäbe und
Vierkant- sowie Rundmaterial (FB) |
 |
| Abb. 05-07-01-06: 6 mm
Kupferstab, die Schnur zeigt die exakte
Ost-West-Richtung an. Als Halterung dienen zwei Holzstäbe mit eingesägen Kerben. Die Positionen der "Beugungsmuster" werden direkt an dem Maßstab ablesen und notiert. (FB) |
 |
| Abb. 05-07-01-07: Überblick Die Verstelleinrichtung mit der Gewindestange ist entfernt, da deren Material zum Teil mit den zu untersuchenden in Resonanz gegangen ist. (FB) |
Durch direktes Ablesen ermittelte Position auf der Skala 24.4.2020
 |
| Abb. 05-07-01-08: 24.4.2020, Daten für den Schwerpunkt einer Struktur (FB) |
25.4. und 26.4.2020
Durch direktes Ablesen ermittelte Position auf der Skala, jeweils für Beginn und Ende eines Strukturelementes
Beginn: Quadrat (Vierkant), Kreis (Rundmaterial) mit durchgezogenen Linien verbunden
Ende: Dreieck, gestrichelte Linien
 |
| Abb. 05-07-01-09: 25.4.2020,
26.4.2020 violett: Kupfer, grün: Messing, gelb: Buchenstab, rot: Aluminium, gelb/rot: Plexiglas blau: Eisen, schwarz: Stahl (FB) |
 |
| Abb. 05-07-01-10: 25.4.2020,
26.4.2020 violett: Kupfer, grün: Messing, gelb: Buchenstab, rot: Aluminium, gelb/rot: Plexiglas blau: Eisen, schwarz: Stahl (FB) |
 |
| Abb. 05-07-01-11: 25.4.2020,
26.4.2020 blau: Eisen, schwarz: Stahl (FB) |
 |
| Abb. 05-07-01-12: Jeweils über die
Abstände zwischen den Werten für "Beginn" gemittelt
und auch über die Differenz von "Beginn" bis "Ende".
Die Breite ist etwas weniger als der halbe Abstand. (FB) |
 |
| Abb. 05-07-01-13: Jeweils über die
Abstände zwischen den Werten für "Beginn" gemittelt
und auch über die Differenz von "Beginn" bis "Ende".
Das Verhältnis von Breite zu Abstand ist etwas kleiner als 0.5 (FB) |
5.7.2 Markierung der Positionen auf Holzbrett
 |
| Abb. 05-07-02-01: Zylinder aus Eisen. Statt direkter Ablesung der Werte wird jetzt zunächst auf dem Holzbrett angezeichnet. So läßt sich auch etwas über die Intensität der einzelnen Elemente notieren. Das Ergebnis ist eine zur Mitte symmetrische Anordnung mit breiten Streifen und einem schmalen (sehr intensiven) Bereich in der Mitte. (FB) |
 |
| Abb. 05-07-02-02: Messing-Zylinder
961 g Im Vergleich zum Eisenzylinder sind die Strukturen feingliedriger. (FB) |
 |
| Abb. 05-07-02-03: Scheibe aus Aluminium,
Struktur ist etwas gröber als bei Messing. (FB) |
 |
| Abb. 05-07-02-04: rechteckig 10 x 20
mm², Kupfer verzinnt (Leiter aus der
Elektrik) (FB) |
 |
| Abb. 05-07-02-05: Stahlflasche
mit Stickstoff (FB) |
 |
| Abb. 05-07-02-06: Steinzeug,
Flasche für Korn (FB) |
 |
| Abb. 05-07-02-07: Weinflasche mit
Wasser gefüllt. Das "Begungsmuster" besteht
aus vielen Elementen. (FB) |
 |
| Abb. 05-07-02-08: Stahlfeder,
"Slinky" (Schraubenfeder, Kinderspielzeug)
(FB) |
 |
| Abb. 05-07-02-09: Prismatischer
Bleiklotz Das "Beugungsmuster" ist unsymmetrisch, die Hauptachse (nach oben) scheint senkrecht zur Austrittsfläche zu sein. In der Hauptrichtung (nach links oben) gibt es eine intensive Mittellinie. (FB) |
 |
| Abb. 05-07-02-10: Prisma aus
Aluminium Das "Beugungsmuster" ist unsymmetrisch, die Hauptachse (nach oben) scheint senkrecht zur Austrittsfläche zu sein. Aber auch in Hauptrichtung (nach links oben) gibt es ein symmetrisches Muster mit intensiver Mittellinie. Abb. 03-03-02: Prisma aus Aluminium, im Hintergrund der Spalt in dem feuchten Karton n-strahlung.htm#kapitel-03-03(FB) |
Ergebnisse: Gegenüberstellung der Holzbretter mit den Markierungen
 |
| Abb. 05-07-02-11: Eisen 55 mm,
Aluminium 120 mm, Heliumflasche 140 mm, Slinky Stahlfeder (FB) |
 |
| Abb. 05-07-02-12: Magnesium 32 mm,
Messing 65 mm; Messing 70 mm Argon-Flasche, 70 mm; CO2 Flasche 70 mm, Steinzeugflasche mit ; ohne Gummistopfen Aluminium Prisma Blei Prisma (FB) |
 |
| Abb. 05-07-0-13: Magnesium 32 mm,
Messing 65 mm; Messing 70 mm Argon-Flasche, 70 mm; CO2 Flasche 70 mm, Steinzeugflasche mit ; ohne Gummistopfen Weinflasche mit Wasser (FB) |
5.8 Linsen
Für die Experimente mit N-Strahlen ( R. Blondlot) wurden Linsen aus Aluminium mit unterschiedlichen Brennweiten angefertigt.
n-strahlung.htm#kapitel-03-02-02
Bei Bestrahlung mit Sonnenlicht gab es bei jeder Linse eine Reihe von "Brennpunkten".
Wiederholung der Linsenexperimente mit "Strahlung" aus der Erde.
28.4.2020
 |
Abb. 05-08-01: 29.4.2016,
Aluminium-Linse, Beleuchtung mit Sonnenlicht von links
obenaus n-strahlung.htm#kapitel-03-02-02 |
 |
| Abb. 05-08-02: Aluminium-Linse R = 65
mm, "Beleuchtung" von rechts unten.
(Richtung der Zentrifugalkraft der Erde.) Mit roten Wäscheklammern sind fünf Positionen erhöhter spürbarer Intensität gekennzeichnet. (FB) |
 |
| Abb. 05-08-03: Aluminium-Linse R = 90
mm rot , blau grün (FB) |
 |
| Abb. 05-08-04: Aluminium-Linse R =
120 mm, Markierungen für rot (R= 66 mm ), blau (R=90 mm), grün (R=120 mm), gelb (R= 150 mm) (FB) |
 |
| Abb. 05-08-05: Alle Markierungen für die gefundenen Positionen bei vier Aluminium-Linsen unterschiedlicher Brennweite (FB) |
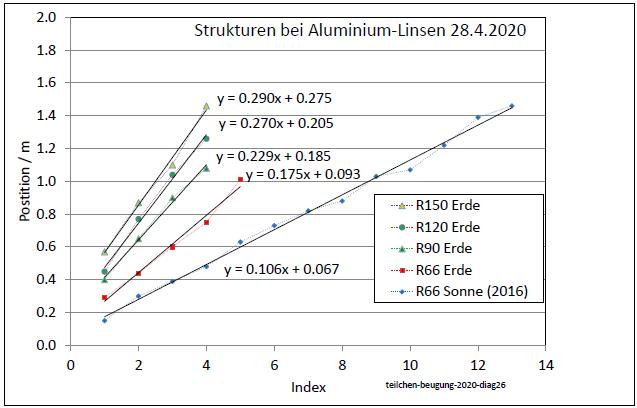 |
| Abb. 05-08-06: Für die mit
Wäschklammern markierten Positionen gelten lineare
Abhängigkeiten. Die Steigungen sind 0.175, 0.229, 0.227 und 0.290 m Die untere Kurve gehört zu den Experimenten mit Sonnenlicht und der R=66 mm Linse. aus n-strahlung.htm#kapitel-03-02-02(FB) |
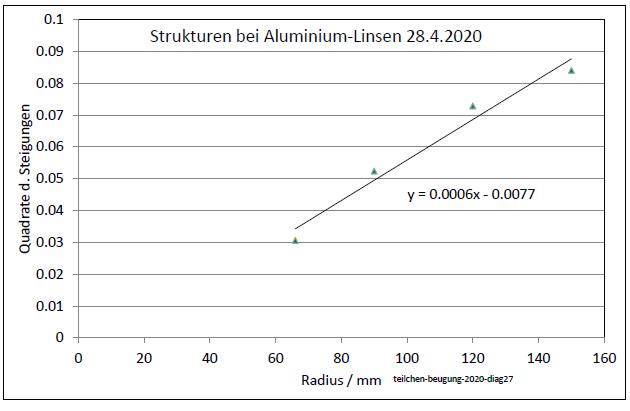 |
| Abb. 05-08-07: Die Quadrate der
Steigungen aus vorheriger Abbildung, aufgetragen
gegen den Radius der Linsen (FB) |
6. Rotierender Zylinder
16.05.2020
bewegte-materie-oszillierend-zwei.htm
Lotrechte Rotationsachse
 |
Abb. 06-00: Ein Messingzylinder mit
961 g rotiert um eine vertikale Achse. Der
Antriebsmotor ist einige Meter davon entfernt.
Antrieb über einen Zahnriemen.aus bewegte-materie-oszillierend-zwei.htm |
Rotationsachse in Richtung der Zentrifugalkraft der Erde
 |
| Abb. 06-01: Ein Messingzylinder
(links) wird über einen Zahnriemen vom Motor
(rechts) angetrieben. Die Motorachse zeigt schräg nach unten in Richtung Norden (in Richtung Vermessungsstange am Zaun) (FB) |
 |
| Abb. 06-02: Die Achse des Drehtellers
ist exakt ausgerichtet für die geografische Breite
49.6° und die Nord-Süd-Richtung (FB) |
 |
| Abb. 06-03: Antrieb über Zahnriemen,
Motor oben links (FB) |
 |
| Abb. 06-04: passend zu vorherigem
Bild: Wenn der Zylinder exakt ausgerichtet ist, gibt
es für "sehende" Beobachter eine Struktur, die etwa
die Form dieser Kerzenflamme hat. Diese Flamme folgt
der Richtung der Drehachse. Jedoch, wenn die Drehachse mit dem Zylinder nur um wenige Grad aus der idealen Richtung geschwenkt wird, verringert sich die Länge der "Flamme". Bei Abweichung von über fünf Grad, ist die Flamme nicht mehr zu beobachten. (FB) |
 |
| Abb. 06-04: Zum Wechel der
Drehrichtung wird nicht umgepolt, sondern lediglich
der Zahnriemen anders aufgelegt. Dann bleiben alle
Strukturen von der Antriebseinrichtung unverändert.
(FB) |
 |
| Abb. 06-05: Ein Stapel von Ringmagneten
zeigt auf den Messingzylinder und dessen
Rotationsachse. Wenn dessen Magnetfeld die gleiche Richtung wie das Erdmagnetfeld hat, wird die "Flamme" angezogen, im umgekehrten Fall abgestoßen oder weggedrückt. (FB) |
 |
| ABb. 06-06: Ein HT Rohr ist mit
seinem "spitzen" Ende gegen die "Flamme" gerichtet.
Sie wird von der Drehachse weg nach links oben
"geblasen". (FB) |
 |
| Abb. 06-07: Dreht man das HT-Rohr um,
dann wird die "Flamme" in das Rohr "gesaugt".
(FB) |
 |
| Abb. 06-08: . . . und es kommt
am anderen Ende des Rohres etwas heraus, daß sich
sogar mit Rohrbögen und Verlängerungen
weiterleiten läßt (wie ein breiter Strahl oder
eine Wolke) Das Rohr wirkt wie ein Wellenleiter. (FB) |
 |
| Abb. 06-09: Mit einem kleinen
Badezimmerventilator wird Luft in das Rohr geblasen. Trotz laufendem Ventilator kommt am Rohrende etwa das Gleicher heraus wie bei ausgeschaltetem Ventilator. (FB) |
 |
| Abb. 06-10: Im Hintergrund rotiert
der Zylinder. Das "Etwas" läßt sich auch durch
weitere Rohrstücke fortleiten. Hier sind in das Rohr
zwei Elemente mit jeweils einer Kupferspule in
axialer Richtung eingefügt. "Resonanzrohr"
(FB) |
 |
| Abb. 06-11: Auf dem Rohr sind etwa 35
Windungen Klingeldraht (FB) |
 |
| Abb. 06-12: 18.05.2020, Spulen
mit Gleichstrom betrieben bei 1.64 μA
d.h. etwa 1 uT. Änderung von 30 mA entspricht 20 μT, das Erdfeld hat etwa 48 μT. erdmagnetfeld.htm (FB) |
 |
| Abb. 06-13: 18.05.2020 Ein kleiner Gleichstrom durch die Spule erzeugt ein sehr schwaches Magentfeld in Richtung des Rohres. Damit läßt sie die Größe der aus dem Rohr austretenden Struktur verändern. Mit zunehmendem Magnetfeld wird die Struktur kürzer. Polt man den Strom um, gibt es überhaupt keinen Strahl, "gesperrt" (FB) |
 |
Abb. 06-14: Modell für eine Strömung
in einer rotierenden Umgebung?aus physik-neu-004.htm#physik-neu-04-2 |
7. Resonanzrohr
7.1 Resonanzrohr im Einsatz
 |
| Abb. 07-01-01: Quelle list ein
rotierender Messingzylinder. Das Rohr "saugt" von
dort ab. Beide Spulen (unten am Boden) sind an eine Wechselspannung angeschlossen. Sie sind entgegengesetzt gepolt. Der Strom fließt in den Spulen in unterschiedlicher Richtung. Durch Einfügen von weiteren Rohrstücken läßt sich der Abstand zwischen Spulen variieren. (FB) |
 |
| Abb. 07-01-02: 18.05.2020 rechts oben
der rotierende Messingzylinder, Antrieb mit grünen
Zahnriemen. Am Ende des Rohres beginnt eine
Meßstrecke zur Ermittlung der Geometrie der
Struktur. (FB) |
 |
| Abb. 07-01-03: Beispiel:
Frequenzgenerator mit 38.5 Hz, 3,4 uA (RMS) und 60
kOhm Vorwiderstand (FB) |
 |
| Abb. 07-01-04: Versuch der Feinverstimmung
über die Rohrlänge. Verschiebung um wenige
Millimeter. (FB) |
 |
| Abb. 07-01-05: Feinverstimmung,
Einfluß der Frequenz auf die Länge der Struktur. Es sieht so aus wie die Resonanzkurve bei einem schwingenden System, das bei vier unterschiedlichen Bedingungen angeregt wird. Der Abstand zwischen den Spulen beträgt rund 1,3 m. Hier wurde es um jeweils 15 mm (rund 1%) verlängert. Die Abstände sind rechnerisch demnach 1.300 m , 1.315 m, 1.330 m, 1.345 m Beobachtung: Die Frequenzmaxima verschieben sich mit zunehmender Länge etwas nach unten. Allerdings ist die Verschiebung (sie liegt im Bereich von einigen Prozent) nicht proportional zur Längenänderung (ebenfalls im Bereich von einigen Prozent). (FB) |
 |
Abb. 07-01-06: Resonanzkurve aus resonanz.htm |
Resonanzrohr im Einsatz
19.05.2020
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-07: Ein Rohr mit einem 87°
Bogen liegt horizonal. Von hinten wird mit einem
Spiegel Sonnenlicht eingestrahlt. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-08: Das Sonnenlicht geht
durch das horizontale Rohr, vorne und
hinten sind die beiden Spulen. Bei 13.6 Hz ist der "Strahl" etwa 5,5 m lang. Es gibt in der Struktur wechselnde Bereiche (20 cm breit mit rund 70 cm Abstand (GE). Fällt kein Licht vom Spiegel durch das Rohr, ist die Struktur äußerst schwach. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-09: Ein Spiegel auf dem
Rasen (rechts) lenkt Sonnenlicht durch das Rohr. Das Rohr ist in Richtung der Zentrifugalkraft der Erde ausgerichtet. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-10: Sonnenlicht scheint
durch das Rohr bis zum Bogenstück oben rechts. (FB |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-10: Aus dem Bogenstück
heraus kommen spürbare Strukturen (Wellen und Zonen)
Das Rohr wirkt wie ein Wellenleiter. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-11: Vorversuch mit
verschiedenen Bögen und Verlängerungen. Das schräge Rohr ist exakt in Richtung der Zentrifugalkraft der Erde ausgerichtet. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-12: Mit einer kleinen
Batterie oder einem Magneten läßt sich der
"Durchsatz" durch das Rohr verändern. Je nach Polung
vergrößert oder verkleinert sich die Länge der am
anderen Rohrende austretenden Strukturen (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-13: 20.05.2020 in dem
ansteigenden Rohr rechts entstehen die Wellen. Es
hat die Richtung der Zentrifugalkraft der Erde. Umlenkung der Strukturen (Wellen) durch mehrer Rohre und Bögen. Auf diese Weise lassen sich die entstandenen Zonen in Bodennähe untersuchen. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-14: 20.05.2020 Es sind die Maße der Zonen für drei unterschiedliche Bedingungen (Frequenzen in den Magnetfeldspulen, 13.6 Hz, 25.9 Hz und 38.8 Hz) mit Holzstäben und Blechtafeln ausgelegt. Die in Längsrichtung liegenden Hölzer markieren die Breite der Zonen bei der unteren Frequenz. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-15: 20.05.2020, es sind
jeweils 4 Zonen. Lage der Blechtafeln (grün) 25.9 Hz und (rot) 38.8 Hz (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-16: schräges Rohr exakt in
Richtung der Zentrifugalkraft der Erde. Auf diese Weise lassen sich auch unterschiedliche Quellen zusammenfügen und damit die Qualität am Ausgang verändern / mischen. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-17: 21.05.2020 Das aufsteigende Rohr ist exakt in Richtung der Zentrifugalkraft der Erde ausgerichtet. Für die Analyse optimierter Aufbau mit langer horizontaler Wegstrecke in Richtung Nord. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-18: Am unteren Rohr sind
die beiden Rohrstücke mit den Magnetspulen
angebracht. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-19: 21.05.2020 Die Meßstrecke: Bei allen vier unterschiedlichen Frequenzen gibt es jeweils Gruppen von vier Zonen, die durch einen Zwischenraum voneinander getrennt sind. Bei den unteren Frequenzen 13.6 Hz, 26.0 Hz und 38.8 Hz sind die Elemente einer Gruppe markiert und bei 129.9 Hz nur jeweils die Gruppen.
Allerdings ist für diese Annahme ein Faktor von etwa 95% zur Grundfrequenz nötig. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 07-01-20: Blick in Richtung zum
Rohr: die Markierungen (FB) |
 |
| Abb. 07-01-21: der Aufbau von oben Bei den unteren Frequenzen 13.6 Hz, 26.0 Hz und 38.8 Hz sind die Elemente einer Gruppe markiert und bei 129.9 Hz nur jeweils die Gruppen. (FB) |
 |
| Abb. 07-01-22: ganze Meßstrecke (FB) |
 |
| Abb. 07-01-23: Anfang der Meßstrecke
(FB) |
 |
| Abb. 07-01-24: Vorbild für die Natur
der Strukturen? Um einen Rosenquarz (roter Quader links) herum: fünf Gruppen von jeweils vier Kissen mit unterschiedlichen Eigenschaften. (schematisch) ähnliche Abbildung wie in quarzrohr-angeregt.htm#kapitel-02-01-01a |
 |
||||||||||||||||||
| Abb. 07-01-25: Daten von Abb.
07-14 (20.05.2020) und Abb. 07-19 (21.05.2020) Die Markierungen der unteren drei Frequenzen 13.6 Hz, 26.0 Hz und 38.8 Hz wurden fortlaufend durchgezählt, wobei die Lücken ebenfalls mit zur Reihe gehören. Bei 129.9 Hz sind es die Positionen einer ganzen Gruppe. ( nur jeder zweiten?) Die Abstände der Elemente (Steigungen der Geraden) sind 1.06 m, 0.57 m, 0.38 m, 0.22 m Dividiert man bei den höheren Harmonischen die Werte durch 95% (Abb. 07-19), dann ergeben sich die Faktoren von nahezu 2, 3 und 5.
Bei der ersten Messung (vom Vortag 20.05.2020) ergeben sich etwas größere Abstände. (FB) |
||||||||||||||||||
 |
||||||||||||||||||
| Abb. 07-01-26: Daten von Abb.
07-14 (20.05.2020) und Abb. 07-19 (21.05.2020) Unter der Annahme, daß es sich um die 2. 3. und 10. Harmonische handeln könnte, wurden die jeweiligen Indizes mit 1; 1/2 ; 1/3 und 1 erhöht. Nun ergeben sich für den 21.05.2020 - wie erwartet - Geraden mit gleicher Steigung. und zwar: 1.11; 1.13;1.18; 1.09 (FB) |
Einfluß der Frequenz
22.05.2020
Symmetrisch zur 2. Harmonischen bei f0=26.0 Hz wurden die Frequenzen
f0 +/- 0.2 Hz und f0+/- 0.4 Hz also 25.6 Hz, 25.8 Hz und 26.2 Hz, 26.4 Hz ausprobiert
Ergebnis: Schon bei einer geringen Abweichung von 0.2 Hz verringern sich die Abstände der Elemente stark.
 |
| Abb. 07-01-27: vom 21.5.2020 Beugungsmuster für die Grundfrequenz 13.6 Hz (Hölzer), die zweite Harmonische 26.0 Hz (grüne Blechtafeln oben) die dritte Harmonische 38.8 Hz (rosa Blechtafeln unten) sowie vom 22.05.2020 (gelbe /rote bzw. grüne/blaue Wäscheklammern) für 26.2 Hz und 26.4 Hz Wie sich herausgestellt hat, sind die Positionen der Zonen für 25.8 Hz; 25.6 Hz etwa so wie bei den beiden anderen Frequenzen oberhalb von 26.0 Hz. (FB) |
 |
| Abb. 07-01-28: Die Positionen für die
2. Harmonische vom 21.05.2020 und 22.05.2020 Frequenzen 26.0 Hz, 26.2 Hz, 26.4 Hz bzw. 25.6 Hz und 25.8 Hz (FB) |
 |
| Abb.07-01-29: Das System reagiert
stark auf Frequenzänderungen bei der Anregung. Bei der "Resonanzfrequenz" von 26.0 Hz ist die "Amplitude"* groß, schon 0.2 Hz (<1%) ist die "Amplitude" auf etwa 50 % abgefallen. Die Halbwertsbreite ist entsprechend 0.4, die Güte etwa Q = 26/0.2 = 130 *Amplitude im Sinne von Ausdehnung der Zonen. (FB) |
7.2 Unterschiedliche Materialien am Eingang des Rohres
21.05.2020
 |
| Abb. 07-02-01: Aluminiumfolie aus der
Küche matte Seite nach innen: Struktur intensiv blanke Seite nach innen: Struktur ganz schwach erzeugt die aufgerauhte Oberfläche neue Teilchen? 21.05.2020 (FB) |
 |
| Abb. 07-02-02: ein Quader aus Wismut
am Eingang des Rohres saugt..... Am Ausgang vom Rohr bewirkt Wismut eine Umlenkung des "Strahls" (FB) |
 |
| Abb. 07-02-03: ein Paar U-förmige
Magnete halten einander fest NiFe? ("saugt"
ab?) Struktur wird schwächer (FB) |
 |
| Abb. 07-02-04: Aluminiumblech oder
Kupferblech vor dem Ausgang: keine Wirkung Eisenzylinder vor dem Eingang : intensiver Batterie neben oder im Rohr: keine Wirkung Nickelblech oder Titanblech neben dem Eingang: Struktur wird schwächer Wolfram oder Tantalblech neben dem Eingang: Struktur wird intensiver Germanium Einkristall -->: intensiver, Germanium Einkristall <-- schwächer Stein mit rotem Aufkleber (Ho): ganze Fläche der Struktur intensiver, auch deren Zwischenräume 21.05.2020 (FB) |
 |
| Abb. 07-02-05: Kristalle aus Pyrit
und Quarz mit der Spitze zur Öffnung, Struktur wird
intensiver (FB) |
 |
| Abb. 07-02-06: Spiralfeder
(Slinky) aktive Seite / entgegengesetzte Seite
zeigen zum Rohr, eine Seite regt an (FB) |
 |
| Abb. 07-02-07: doppelwandiges
Isolierglas (evakuiert) vor dem Rohr-Eingang, hat
keinen Einfluß, Struktur verändert sich kaum. (Teilchen gehen hindurch) Kommentar 04.08.2020: dreht man das Isolierglas um 180°, dann sperrt es. (FB) |
 |
| Abb. 07-02-08: doppelwandiges
Isolierglas (evakuiert) vor dem Rohr-Ausgang Struktur ist verschwunden. (Wellen gehen nicht hindurch) Kommentar 04.08.2020: dreht man das Isolierglas um 180°, dann ist es durchlässig. (FB) |
 |
| Abb. 07-02-09: doppelwandiges
Isolierglas (evakuiert) vor dem Rohr-Ausgang Damit ist der Ausgang vom Rohr für Wellen versperrt. Es bilden sich keine Strukturen dahinter aus. Kommentar 04.08.2020: dreht man das Isolierglas um 180°, dann ist es durchlässig. (FB) |
8. Ringe und Spulen
22.05.2020
 |
| Abb. 08-01: Ring aus Kupferrohr 15 mm
und Stahlfeder. Exakt in Richtung der
Zentrifugalkraft ausgerichtet. Beide Enden vom Kupferrohr sind mit einer Muffe zusammengesteckt. Es gibt starkt spürbare Strukturen, deren Intensität mit der Kombination der Ziehrichtungen der Materialien variieren. Sehr intensiv! Nur kurze Zeit ausprobieren!!! (FB) |
 |
| Abb. 08-02: Ring aus Kupferrohr,
Enden nicht miteinander verbunden, aber mechanischer
(elektrischer) Kontakt. schwache Struktur (FB) |
 |
| Abb. 08-03: Ring aus Kupferrohr,
beide Enden mit einer Muffe verbunden, es entsteht eine riesige Struktur, die mit der Zeit anwächst. (selbstverstärkende "Strömung" im Innenraum des Rohres?) Der Ring hat zwei Seiten, er ist "gerichtet", wie ein aktiver Körper. (FB) |
 |
| Abb. 08-04: Hula-Hupp-Reifen, Seite A
und Seite B haben unterschiedliche Wirkungen (FB) |
 |
| Abb. 08-05: beide Ringe in
Kombination. Je nach Ausrichtung gibt es Verstärkung
oder Abschwächung. (FB) |
 |
| Abb. 08-06: Kabeltrommel in exakter
Ausrichtung Wenn die Drähte offen sind, dann gibt es keine Struktur. Verbindet man sie (Kurzschluß), dann gibt es eine große Struktur in Richtung Süden. (FB) |
 |
| Abb. 08-07: Widerstand 0.9 Ohm, die
Art wie die drei Adern im Kabel miteinander
verbunden sind, verändert die Intensität (Größe) der
Struktur. (FB) |
 |
| Abb. 08-08: Transformatorspule, 23000
Windungen, wenn kurzgeschlossen, dann große Struktur
nach Süden, wenn offen, dann keine. Dreht man die Richtung der Spule (Anschlüsse nach Norden ), dann ist im Süden keine Struktur vorhanden. (FB) |
 |
| Abb. 08-09: Bei dieser Spule mit 500
Windungen ist es bezüglich der Richtung umgekehrt.
(FB) |
 |
| Abb. 08-10: Ringkerntrafo mit
mehreren Wicklungen und Eisenkern. genau umgekehrt: wenn alle Wicklungen offen sind, dann gibt es nach Süden eine große Struktur. wenn nur eine Wicklung kurzgeschlossen ist, keine Struktur 22.05.2020 (FB) |
9. Effekte durch natürliche Anregung
9.1 Durchstrahlung
L. Straniak
Die achte Großkraft der Natur, (1936)
 |
| Abb. 09-01-01: Glaskugel (FB) |
 |
| Abb. 09-01-02: Strukturen um die
Glaskugel herum, wie ein vierblättriges Kleeblatt,
in den Hauptachsen ist nichts, in den
Zwischenrichtungen das Grün. Blick von Süden nach Norden. (FB) |
 |
| Abb. 09-01-03: Blick von Osten nach
Westen (FB) |
 |
| Abb. 09-01-04: Blick von Norden nach
Süden (FB) |
 |
| Abb. 09-01-05: aus dünnem Kupferrohr
gebogen (FB) |
 |
| Abb. 09-01-05a: Blätter vom
Gingko-Baum haben in der Mitte einen Einschnitt.
(FB) |
 |
| Abb. 09-01-05b: siehe seums.htm (FB) |
 |
| Abb. 09-01-05c: siehe seums.htm (FB) |
 |
| Abb. 09-01-06: auch bei diesem
Kalkstein (Jura) ist die Struktur ähnlich wie bei
der Glaskugel. (FB) |
 |
| Abb. 09-01-07: gilt auch für diesen
roten Stein mit SE (FB) |
 |
| Abb. 09-01-08: ebenfalls bei dieser
Goldkette ist die Struktur ähnlich, die Stromkontakte sollen hier keine Rolle spielen. (FB) |
 |
| Abb. 09-01-09: auch beim Würfel aus
Graphit. Stromkontakte sollen hier keine Bedeutung
haben. (FB) |
9.2 SEUMS
siehe auch seums.htm
 |
| Abb. 09-02-01: Strukturen um einen
Würfel aus Graphit, 12 cm Kantenlänge (FB) |
 |
| Abb. 09-02-01a: von innen nach außen
liegen die Markierungen (grüne Holzstäbe) jeweils
für die Abweichungen von der exakten
Nord-Südrichtung und zwar für 0°, 1°, 2°, 3°, 4° und
5°. |
 |
| Abb. 09-02-01b: mit der 1 m
langen Holzlatte läßt sich die Richtung vom
Würfel exakt "steuern". (FB) |
 |
| Abb. 09-02-02: Graphit-Würfel auf dem
Drehteller, Buchendübel als Zapfen (FB) |
 |
| Abb. 09-02-03: Von Strich zu Strich
auf der Skala sind es 1 °. (FB) |
 |
| Abb. 09-02-04: die doppelten
Holzmarkierungen links oben vor dem Baum gehören zu
den Verstellwinkeln 3°, 4° und 5,
bzw. -3°, -4° und -5° (FB) |
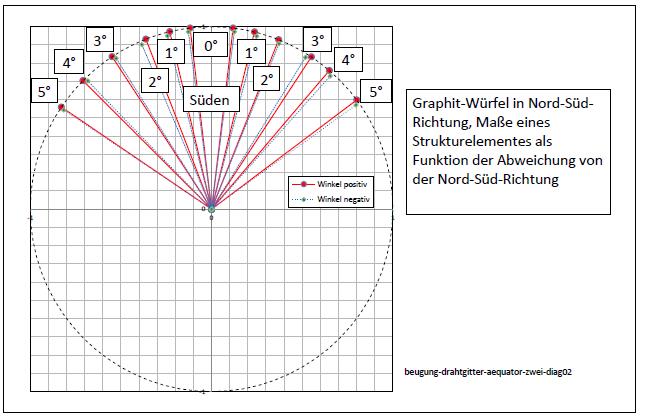 |
| Abb. 09-02-05: |
 |
| Abb. 09-02-06: Position der
ausgelegten Hölzer für die Winkel 0 bis 5 ° und 0
bis -5° Die gemessenen Positionen sind symmetrisch zur Süd-Richtung. z.B. erzeugt die Drehung auf 4° die gleiche Verschiebung wie auf -4°. (FB) |
 |
| Abb. 09-02-07: zusätzliche Neigung
(geografische Breite). Die FLächen 1 und 3 sind
jetzt exakt senkrecht zur Zentrifugalkraft der Erde
ausgerichtet. Beobachtungen von GP: Von der Seite gesehen, kommt aus der Fläche 1 eine lange Struktur heraus, GP: " wie ein Feuerwehrschlauch", außen um die Achse 1-3 herum, gibt es einen Torus. Vermutlich ist 1-3 die Richtung beim Pressen des Graphitpulvers gewesen GP: schon bei kleinsten Verdrehung verkleinert sich der Torus. Aus der Fläche 3 kommt eine "Fontäne" heraus. Liegt der Würfel horizontal mit Fläche 1 oben, GP: gibt es einen "runden Ball" mit 1,8 m Radius. Aus der Fläche 1 "strömt" etwa heraus. (FB) |
 |
| Abb. 09-02-08: Geode (
Druse ), mit Hohlraum, ähnliche Struktur wie
Graphitwürfel. (FB) |
Die Systeme Graphitwürfel oder Kondensatorplatten verhalten sich wie eine Linse:
Der Strahlverlauf ist bei
- achsenparalleler Einstrahlung schmal (d.h. scharf),
- schräger Einstrahlung aufgeweitet (d.h. mit Abbildungsfehlern).
9.3 Anregung mit Objekten
aktive-elemente.htm
konische-koerper-kurz.htm
 |
| Abb. 09-03-01: Shape-Power,
Formeffekte Aus konischen Körpern und auch Dioden (Kapitel-01) kommen Teilchen heraus, die sich mit elektrischen und/oder magnetischen Feldern ablenken lassen. aus smart-dgeim-heidelberg-2018-04-23_07.pdf konische-koerper-kurz.htm (FB) |
 |
| Abb. 09-03-02: Ablenkung im
elektrischen Feld aus smart-dgeim-heidelberg-2018-04-23_07.pdf |
 |
| Abb. 09-03-03: Ablenkung im
Magnetfeld einer Spule aus smart-dgeim-heidelberg-2018-04-23_07.pdf (FB) |
 |
| Abb. 09-03-04: Anregung mit
Lichtbündeln, Sonnenlicht und zwei Spiegel (FB) |
 |
| Abb. 09-03-05: zwei Lichtbündel
fallen auf den Würfel, die Struktur erweitert sich
(FB) |
 |
| Abb. 09-03-06: von innen nach außen:
ohne Anregung, mit einem Lichtbündel, mit zwei Lichtbündeln (FB) |
 |
| Abb. 09-03-07: mit einem Laserpointer
(FB) |
 |
| Abb. 09-03-08: Helmholtzspule,
Kupferdraht mit Seide umsponnen. Wenn die Schlußdrähte offen sind, gibt es eine Verbreiterung der Struktur, wenn kurzgeschlossen, dann keine (FB) |
 |
| Abb. 09-03-09: Pluspol einer Batterie
(FB) |
 |
| Abb. 09-03-10: Minuspol einer
Batterie, Skala zum Einstellen der Entfernung. siehe seums.htm (FB) |
 |
| Abb. 09-03-11: Minuspol zeigt zum
Würfel (FB) |
 |
| Abb. 09-03-12: Zwei Messingstäbe 3 mm
mit gleicher Orientierung zeigen zum Würfel Deren Wirkung verstärkt sich, legt man sie antiparallel, dann gibt es keine Wirkung. (FB) |
 |
| Abb. 09-03-13: Die Enden dieses
aktiven Körpers (Gurke) haben unterschiedliche
Wirkungen auf den Würfel (FB) |
 |
| Abb. 09-03-14: Versuch mit einem
Magneten und unterschiedichen Abständen zum Würfel siehe seums.htm (FB) |
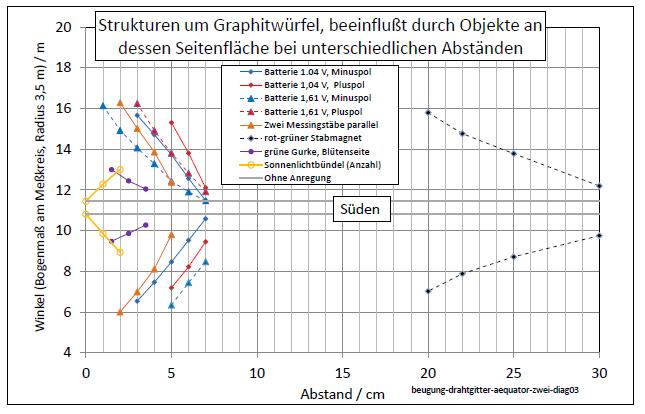 |
| Abb. 09-03-15: Der Einfluß
verschiedener Objekte auf den Würfel als Funktion
des Abstands. Der Stabmagnet hat eine höhere Reichweite als Batterie, Messingstäbe oder Gurke. Für die gelbe Kurve müßte die X-Achse anders beschrift sein: Anzahl der Bündel aus Sonnenlicht. Die Wirkung auf den Würfel nimmt mit der Anzahll zu . siehe seums.htm (FB) |
Wismut, konische Körper
 |
| Abb. 09-03-16: Reibt man den
Stabmagneten mit einem Stück Wismut ab, dann
ist dessen Einfluß auf den Graphitklotz sehr viel
geringer: nur noch etwa 20 mm , vorher
waren es 200 mm. aktive-elemente.htm#kapitel-01-02 wismut.htm Neues Experiment noch zu probieren: Zeitverhalten nach dem "Löschen" (FB) |
 |
| Abb. 09-03-17: Das Stück Wismut
am Graphitklotz läßt die Strukturen verschwinden.
(FB) |
 |
| Abb. 09-03-18: ein konischer Körper
aus Edelstahl, kurzer Abstand (FB) |
 |
| Abb. 09-03-19: zwei Konische Körper
aus Aluminium, entgegengesetzte Anordnung, schwache
Wirkung (FB) |
Schlüsselexperiment,
 |
| Abb. 09-03-20: Zwei Aluminiumbleche
anstatt Würfel. Anreger ist ein Messingzylinder mit
Thermoelement. (FB) |
 |
Abb. 09-03-20a:aus aktive-elemente.htm#kapitel-01-03 |
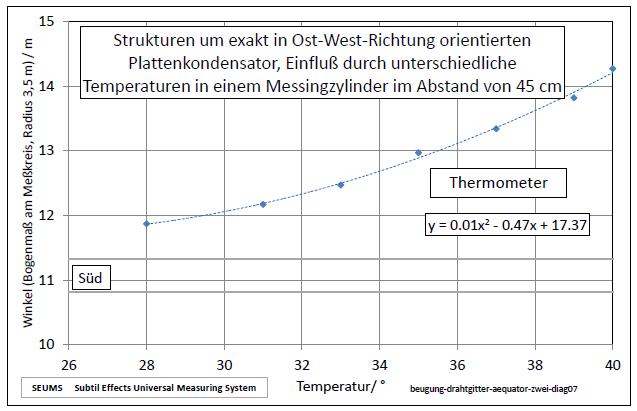 |
 |
Abb. xxaus aktive-elemente.htm#kapitel-01-03 |
 |
Abb. 09-03-21:
aus aktive-elemente.htm#kapitel-01-03 |
Thermospannung !!!!!!! als Folge der Fransen !!!!!??????????????????
9.4 Anregung mit elektrischem Feld
Beim Aufbau ist die Walzrichtung der Bleche zu beachten.
Gleichspannung, Plattenkondensator
 |
| Abb. 09-04-01: Die Platten sind mit
Krokodilklemmen verkabelt. (FB) |
 |
| Abb. 09-04-02: Gleichspannung. Versorgung aus USB-Power-Bank und Spannungsregler auf 10 V, danach Spannungsteiler (FB) |
 |
| Abb. 09-04-03: unterschiedliche
Spannungen innen/ außen, plus / minus zeigt
gegenläufiges Verhalten siehe seums.htm (FB) |
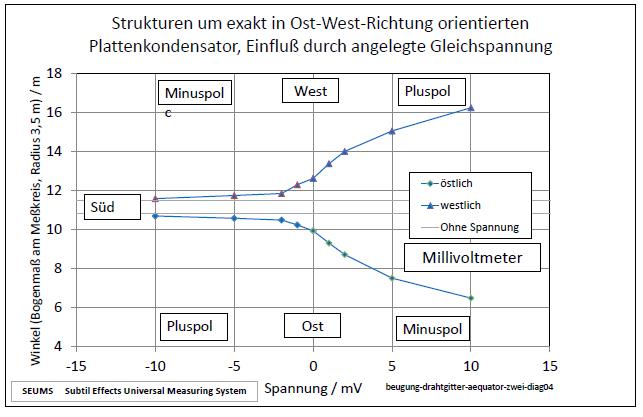 |
| Abb. 09-04-04: Das Verhalten ist
bezüglich Ost- und Westseite symmetrisch, jedoch
bringt ein anderes Vorzeichen bei der Spannung eine
starke Änderung. (FB) |
 |
| Abb. 09-04-05: Verstellung um
1, 2 und 3 Grad (Anzahl der
Wäscheklammern) plus/minus (FB) |
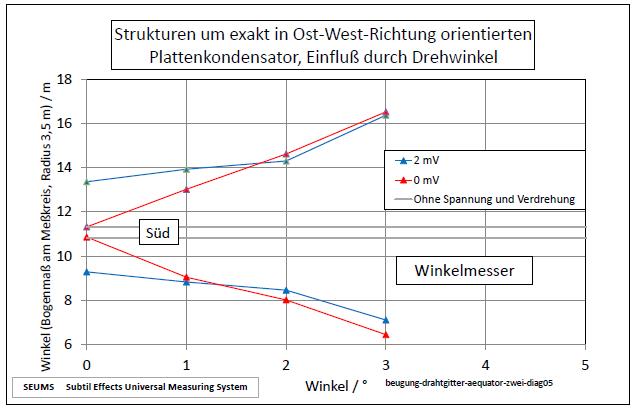 |
| Abb. 09-04-06: Verdreht man die
Ausrichtung der Platten nur wenige Grad, dann ändert
sich die Breite der Struktur. Bei angelegter
Spannung ist der Effekt größer. (FB) |
 |
| Abb. 09-04-06: Feinverstellung, jeder
Strich ein Grad. (FB) |
Wechselspannung, Plattenkondensator
 |
| Abb. 09-04-06: Wechselspannung 13.6
Hz, Spannungsteiler 1 Ohm zu 10 000 Ohm , und
Spannungsteiler 0.1 Ohm zu 10 MOhm ergibt bei 1 Volt Eingangsspannung 10-12 Volt. bei 0.1 Volt eingangsspannung 10-13 V (FB) |
zwei parallele Stäbe Wechselspannung
 |
| Abb. 09-04-07: |
 |
| Abb. 09-04-08: |
 |
| Abb. 09-04-09: |
  |
| Abb. 09-04-10: Rechteck: 14.0
Hz, rund: unten 13.8 Hz, in der
Mitte 13.6 Hz, oben 13.5 Hz |
 |
| Abb. 09-04-11: Lichtbündel |
 |
| Abb. 09-04-12: |
 |
| Abb. 09-04-13: |
10. Sonstiges Aktive Körper, Maxwell-zwei
11.06.2020 mit GP
 |
| Abb. 10-01: Übliche Anwendung,
Transformatorkern (Joch) und Kupferspulen Wenn die linke Spule mit 46 Windungen auf das Joch gesetzt wurde (so wie die rechte gerade ist), dann gibt es "sichtbar" eine rotierende Struktur um die Spulenachse von oben gesehen: CCW (Beschriftung auf dem Kopf) und CW (Beschriftung richtig) Bei der anderen Spule mit 250 Windungen ist bei dieser Anordnung fast keine Rotation zu erkennen. (FB) |
 |
| Abb. 10-02: Die Gurke ändert ihre
spürbaren Eigenschaften, wenn sie durch die Öffnung
im Joch geschoben wurde. Die äußere Struktur eines
aktiven Körpers wird "abgestreift". Wenn man sie anschließend an beiden Enden mit den Händen berührt, ist die Struktur wieder vorhanden. Man kann dann den Vorgang wiederholen. Mit mehrmaligem Hin- und Herschieben verändert sich die Struktur der Gurke und auch die des Lochs im Joch. mögliche Variationen: Gurke hinschieben, mit Händen aktivieren, zurückschieben, verschiedene Kombinationen. Blütenseite, Stängelseite ...., Vorderseite / Rückseite Joch Mehrmals hinschieben, aktivieren, hinschieben..... (FB) |
 |
| Abb. 10-03: Auch beim Durchgang durch
den Gummi-Dichtring von einem 100-er HT-Rohr
passiert das Gleiche. Die Struktur an der Spitze
wird abgestreift. Die Gurke bekommt eine "Aura". Die Struktur an der Spitze kommt nach Berühren mit den Händen wieder. Es entsteht eine Struktur beim Gummiring: Schiebt man die Gurke mehrmals mit Auffrischen durch die Hände hindurch, verlängert sich die Struktur vom Gummi beim zweiten mal um 10 cm. Beim dritten mal ändert sie sich nicht mehr. (FB) |
 |
| Abb. 10-04: Mit einem Stück Wismut
läßt sich die Struktur "abwischen". wismut.htm (FB) |
 |
| Abb. 10-05: Auch beim Durchreichen
der Gurge durch diese Klebeband-Rolle passiert das
Gleiche. (FB) |
 |
| Abb. 10-06: Gilt auch für das
geschweißte Eisenrohr (FB) |
 |
| Abb. 10-07: Mit der Stahlwolle
verkleinert sich die Struktur um das Eisenrohr (FB) |
 |
| Abb. 10-08: Geode läßt sich mit Gurke
"aufladen", wird nach einiger Zeit aber schwächer.
Nach Abwischen mit der Edelstahlwolle wird die
Aufladung schwächer, sie verschwindet nach 2- 3
Wiederholungen. (FB) |
 |
| Abb. 10-09: Lakhovsky-Spule , sehr
intensiv nach oben, mit Wismut "entschärft", mit
Handauflegen keinen "Wiederbelebung" möglich. (FB) |
Literatur: b-literatur.htm
 |
www.biosensor-physik.de | (c)
05.12.2015 - 02.08.2025 F.Balck |


